【JS】分而治之, 逐个击破

• Z时代
• 2024-01-10
• 分类：技术分享

什么是分治算法

将手头的问题分成较小的子问题，然后分别解决每个子问题。如果子问题没办法解决，将子问题划分为更小的子问题时，到达无法划分的阶段时得出结果。最后合并所有子问题的解决方案，以获得原始问题的解决方案。

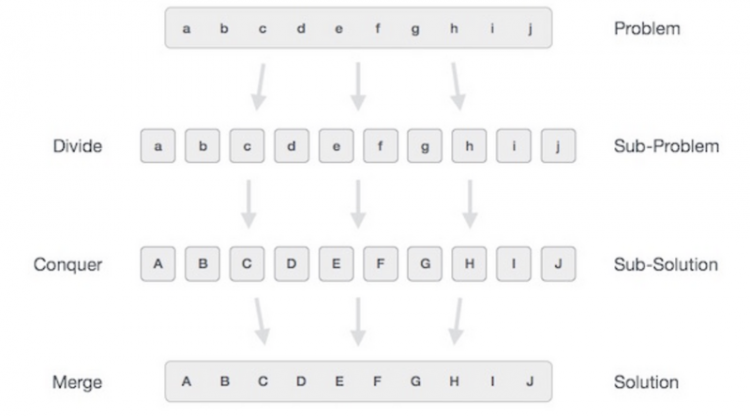
1. 分割，将问题分割为较小的子问题，通常采用递归的形式，直到没有子问题可以进一步分割为止。
2. 解决，当问题无法分割，此时应该已经得到了子问题的答案。
3. 合并，解决了较小的子问题后，此阶段将它们递归组合，得到原始问题的答案。

分治算法可以解决什么问题？

1. 归并排序
2. 快速排序
3. 二分查找

等等

满足使用分治算法的条件

使用分治算法满足的条件：

1. 原问题可以分解为若干个规模较小的子问题
2. 子问题互相独立
3. 子问题的解合并处理后可得到原问题的解

🎉😄 53.最大子序和

思路

将原问题分解为3个子问题，最大子序和要么在数组的左边，要么在数组的右边，要么横跨数组中间。，我们通过递归拆解子问题。

当我们把问题拆解成，数组的长度只有1时，我们就可以得到子问题的解。因为此时最大的子序和就是数组中元素的值。我们只需要返回，数组的左边，数组的右边，或者横跨数组中间的最大值即可，这些子问题的解答，最终会组合成原问题的解。

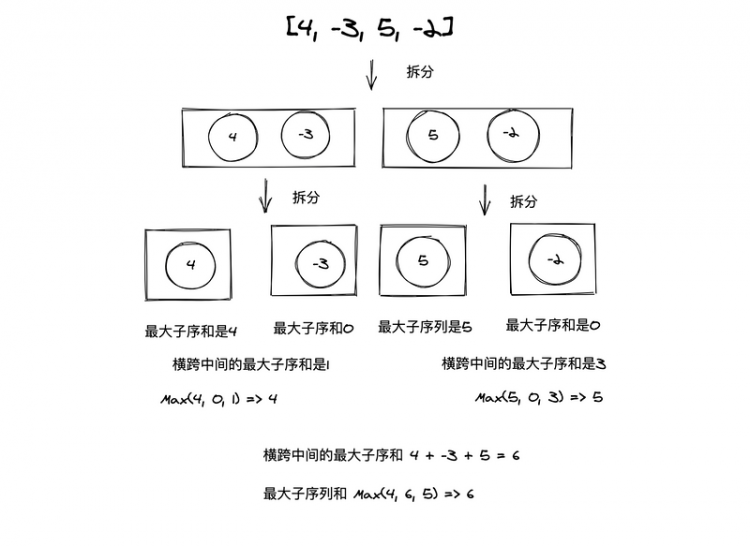
举一个例子🌰, 求[4, -3, 5, -2]的最大子序和。下图是分解的过程

把思路变为代码时，会有一个问题，左右两边可以通过递归获取最大值，如何获取中间的最大值呢？下面是方法的介绍

先计算左边序列里面的包含最右边元素的子序列的最大值，也就是从左边序列的最右边元素向左一个一个累加起来，找出累加过程中每次累加的最大值，就是左边序列的最大值，按照同样的方法，找出右边序列的最大值，左右两边的最大值相加，就是包含这两个元素的子序列的最大值。

解答

/**
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function(nums) {
/**
* 求跨越中间的最大值
*/
const getMiddMax = (left, right) => {
let leftMax = Number.MIN_SAFE_INTEGER
let rightMax = Number.MIN_SAFE_INTEGER
let leftSum = 0
let rightSum = 0
for (let i = left.length - 1; i >= 0; i--) {
leftSum += left[i]
leftMax = Math.max(leftSum, leftMax)
}
for (let i = 0; i < right.length; i++) {
rightSum += right[i]
rightMax = Math.max(rightSum, rightMax)
}
return rightMax + leftMax
}
const divideAndConquer = (arr) => {
if (arr.length <= 1) {
// 得到了最小子问题的解答
return arr.length === 1 ? arr[0] : Number.MIN_SAFE_INTEGER;
}
// 继续拆解子问题
const middIndex = Math.floor(arr.length / 2)
const left = arr.slice(0, middIndex)
const right = arr.slice(middIndex)
const middMax = getMiddMax(left, right)
const leftMax = divideAndConquer(left)
const rightMax = divideAndConquer(right)
return Math.max(middMax, leftMax, rightMax)
}
return divideAndConquer(nums)
};

其他题解

🎉😄 215.数组中的第K个最大元素

思路

本题的解答的思路有很多种。最简单的是使用语言内置的排序，将数组排序后返回第K个最大元素（但是这样刷题也没有任何意义）。
其他的思路是可以利用堆这种数据结构，最小堆，最大堆都可以。因为堆的顶部，永远是最大值或者最小值。

我们重点说一下分治的思路，有点类似快排，但是我们不会像快排一样对整个数组进行排序。只对部分内容进行排序。

取数组的第一个值为基准值，大于它的放在左边，小于它的放在右边。我们的目标是获取数组中的第K个最大元素，如果左边的数组的长度大于K，说明K肯定在左边的数组。如果K的长度大于左边的数组，说明K肯定在右边的数组。

在下一次迭代中，我们可以只处理K所存在的那半边的数组。当数组的长度等于1时就是K了。过程分解如下

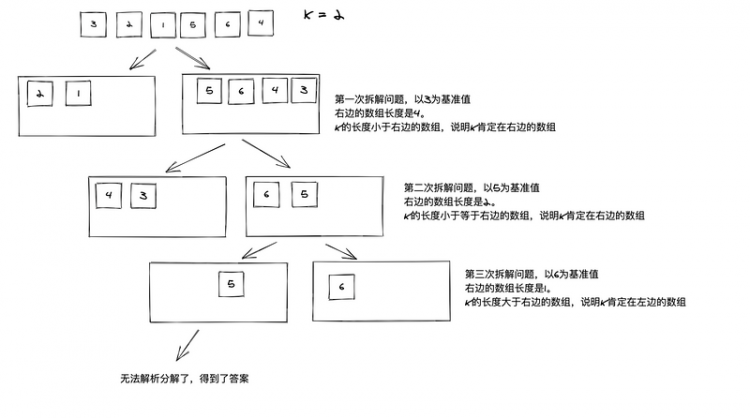
解答

/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function(nums, k) {
let result = null
const divideAndConquer = (arr, base) => {
if (arr.length === 1) {
result = arr[0]
return
}
const referenceValue = arr[0]
const min = []
const max = []
for (let i = 1; i < arr.length; i++) {
if (arr[i] > referenceValue) {
max.push(arr[i])
} else {
min.push(arr[i])
}
}
max.push(referenceValue)
const maxLen = max.length + base;
if (maxLen >= k && max.length) {
// 说明k存在在max数组中
divideAndConquer(max, base)
} else if (maxLen < k && min.length) {
// 说明k存在在min数组中
divideAndConquer(min, maxLen)
}
}
divideAndConquer(nums, 0)
return result
};

🎉😄 169.多数元素

思路

对半拆分数组。如果多数元素的长度大于数组的1/2。那么多数的元素，肯定是拆分出来的两个数组，中的至少其中一个数组中的众数（如果多数元素主要集中在数组的中间部分，则拆分出来的两个数组的众数都是多数元素）。

使用对半拆分的思路，分解子问题：

1. 当子问题（数组）被分解为长度为1时，那么子问题的解（子数组的众数）就是数组中的唯一值
2. 当子问题（数组）被分解为长度为2时，如果数组中两个元素相等那么众数就是该元素。如果数组中两个元素不相等，可以看作子问题没有解。

• 当左边数组的没有解，右边数组有解时，数组的多数元素就是右边数组的众数
• 当左边数组的有解，右边数组没有解时，数组的多数元素就是左边数组的众数
• 当左边数组的有解，右边数组有解，并且解相同时，数组的多数元素就是两边数组相同的解
• 当左边数组的有解，右边数组有解，并且解不相同时，此时我们需要遍历数组计数，得到那一个解才是真正的众数。

下面是一个例子，展示了拆解子问题的过程：

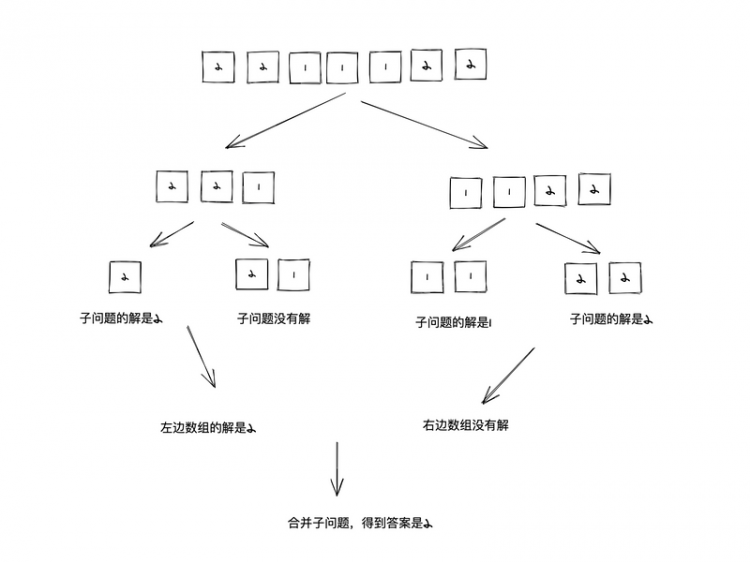
解答

/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function(nums) {
const counter = (arr, target) => {
let count = 0
for (let i = 0; i < arr.length; i++) {
if (arr[i] === target) {
count += 1
}
}
return count
}
const divideAndConquer = (arr) => {
if (arr.length === 1) {
return arr[0]
}
if (arr.length === 2) {
if (arr[0] === arr[1]) {
return arr[0]
} else {
return null
}
}
const middIndex = Math.floor(arr.length / 2)
const left = arr.slice(0, middIndex)
const right = arr.slice(middIndex)
const leftMode = divideAndConquer(left)
const rightMode = divideAndConquer(right)
if (leftMode === null && rightMode !== null) {
return rightMode
} else if (leftMode !== null && rightMode === null) {
return leftMode
} else if (leftMode === null && rightMode === null) {
return null
} else {
// 需要判断下记数
let counterLeft = counter(arr, leftMode)
let counterRight = counter(arr, rightMode)
return counterLeft > counterRight ? leftMode : rightMode;
}
}
return divideAndConquer(nums)
};

😄 241.为运算表达式设计优先级

思路

本题在最后的合并子问题的解时。不像其他分治算法的题目，把子问题的解简单的累加，或者取最大值。本题需要对子问题进行排列组合，取得原始问题的解。

遍历字符串，遇到运算符就将字符串分割成两部分，然后为分割出来的两部分添加小括号。分解子问题，直到被风格出来的部分不包含运算符为止。然后把子问题进行排列组合，得到最终的解答。

下面是分解的过程:

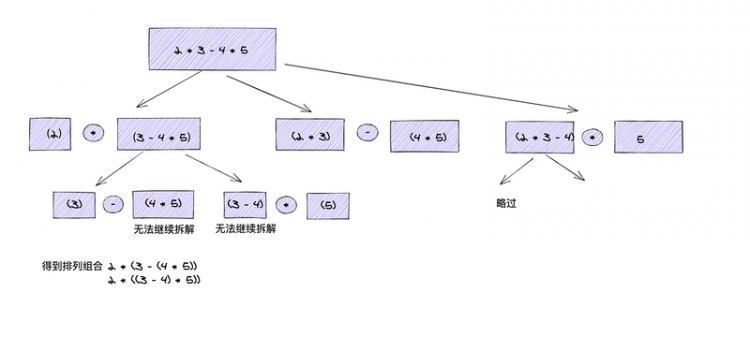
解答

/**
* @param {string} input
* @return {number[]}
*/
var diffWaysToCompute = function(input) {
const result = []
const operatorHash = {
'+': true,
'-': true,
'*': true,
}
// 获取排列组合
const getPermutations = (a, b, operator) => {
const hash = {}
const result = []
for (let i = 0; i < a.length; i++) {
for (let j = 0; j < b.length; j++) {
const key = `((${a[i]})${operator}(${b[j]}))`
if (!hash[key]) {
result.push(key)
}
}
}
return result
}
const divideAndConquer = (str, res) => {
for (let i = 0; i < str.length; i++) {
const operator = str[i]
if (operatorHash[operator]) {
const left = str.slice(0, i)
const right = str.slice(i + 1)
const leftRes = []
const rightRes = []
if (isNaN(Number(left))) {
divideAndConquer(left, leftRes)
} else {
leftRes.push(left)
}
if (isNaN(Number(right))) {
divideAndConquer(right, rightRes)
} else {
rightRes.push(right)
}
res.push(...getPermutations(leftRes, rightRes, operator))
}
}
}
divideAndConquer(input, result)
// 如果是纯数字的情况
if (result.length === 0) {
return [Number(input)]
}
return result.map(item => eval(item));
};

😄 395.至少有K个重复字符的最长子串

思路

本题思路，先找到不可能的字符（在字符串中，少于K次的字符串），用它们分割数组（因为如果包含它们子串就不可能符合要求）。

将分解出的字符串代入下一次迭代。如果在迭代时发现，不存在不可能的字符的字符，这个字符串就是我们的解。结果取解中长度最大的即可。

下面是分解过程：

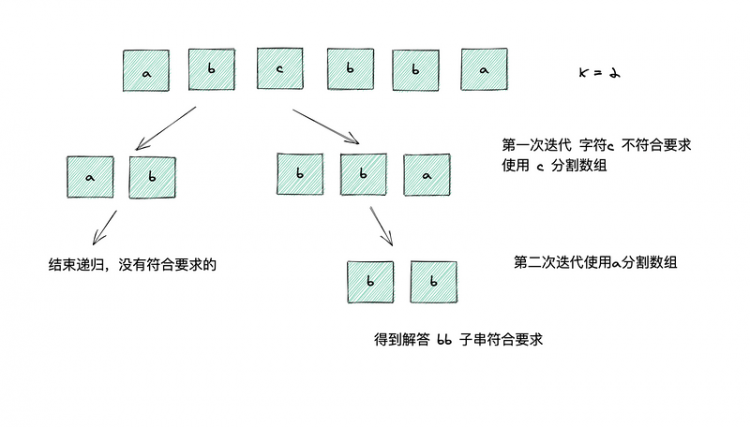
解答

/**
* @param {string} s
* @param {number} k
* @return {number}
*/
var longestSubstring = function(s, k) {
if (s.length < k) {
return 0
}
let result = Number.MIN_SAFE_INTEGER;
const getSplitDots = (str) => {
let splitDots = []
const hash = new Map()
for (let i = 0; i < str.length; i++) {
const key = str[i]
if (!hash.has(key)) {
hash.set(key, [i])
} else {
const val = hash.get(key)
hash.set(key, [...val, i])
}
}
const entries = hash.entries()
for (let [key, value] of entries) {
if (value.length < k) {
splitDots = [...splitDots, key]
}
}
return splitDots
}
const divideAndConquer = (str) => {
// 切割的点
let splitDots = getSplitDots(str)
if (splitDots.length === 0) {
result = Math.max(result, str.length);
} else {
const arr = str.split(splitDots[0])
for (let i = 0; i < arr.length; i++) {
divideAndConquer(arr[i])
}
}
}
divideAndConquer(s)
return result;
};

😄 973.最接近原点的K个点

欧几里得距离的公式

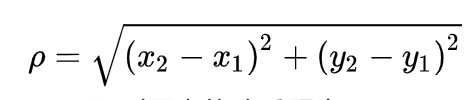
思路

和215题类似，类似快排但是我们不会对全部的内容进行排序。取数组的第一个值为基准值，求出该点的欧几里得距离，以该店的欧几里得距离为基准值，大于基准值放到右边的数组。小于基准值的放到左边的数组。

• 如果K等于左边数组的长度，说明左边的数组就是我们的答案。
• 如果K大于左边数组的长度，说明左边的数组都是我们的答案，但是还有一部分的答案在右边的数组中。在下一次迭代时，我们只需要迭代右边的数组。
• 如果K小于左边数组的长度，说明左边数组中包含了我们的答案，但是还有部分的点，不是我们的答案。右边的数组中，不会包含我们的答案。在下一次迭代时，我们需要迭代左边的数组。

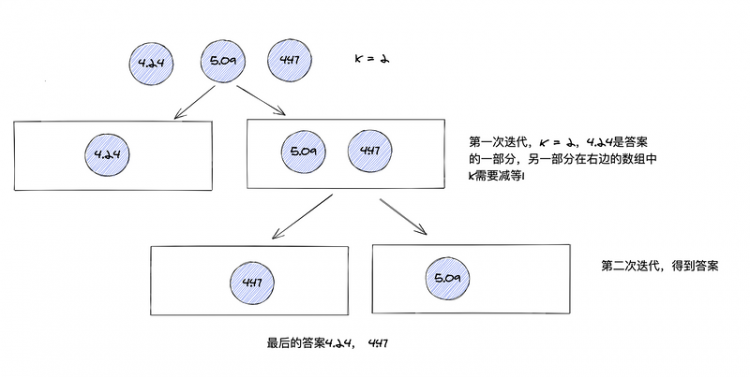
下面以[[3,3],[5,-1],[-2,4]]为例子做一个简单的图解：

• [3,3]的欧几里得距离，4.24

• [5,-1]的欧几里得距离，5.09

• [-2,4]的欧几里得距离，4.47

解答

/**
* @param {number[][]} points
* @param {number} K
* @return {number[][]}
*/
var kClosest = function(points, K) {
let reuslt = []
// 欧几里得距离
const getEuclideanDistance = (o1) => {
const [x1, y1] = o1;
const x2 = 0;
const y2 = 0
return Math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2);
}
const divideAndConquer = (arr) => {
if (!!arr.length && K) {
const benchmark = getEuclideanDistance(arr[0])
const left = []
const right = []
for (let i = 1; i < arr.length; i += 1) {
if (getEuclideanDistance(arr[i]) < benchmark) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
if (left.length) {
right.push(arr[0])
} else {
left.push(arr[0])
}
const len = left.length;
if (K === len) {
K -= len
// K个点都在left中，结束递归
reuslt = [...reuslt, ...left];
} else if (K < len) {
// k个点都在left中，但是left中还有多余的点，需要排查
divideAndConquer(left)
} else {
// left中都是最近的点，还有一部分在right中，需要查找right
K -= len
reuslt = [...reuslt, ...left]
divideAndConquer(right)
}
}
}
divideAndConquer(points)
return reuslt;
};

🎉😄 43.字符串相乘

分治乘法

Karatsuba乘法是一种快速乘法。此算法在1960年由Anatolii Alexeevitch Karatsuba 提出，并于1962年得以发表。此算法主要用于两个大数相乘。普通乘法的复杂度是n2，而Karatsuba算法的复杂度仅为3n^log3≈3n^1.585（log3是以2为底的）

下面使用Karatsuba乘法分解下 5678 * 1234 的过程

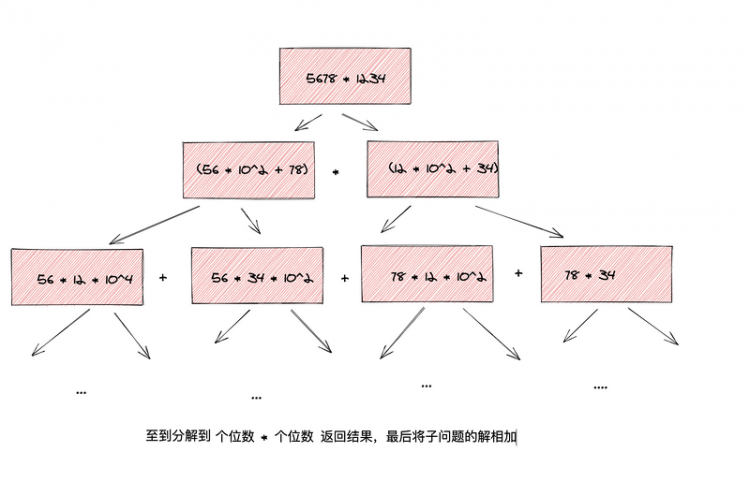
思路

合并子问题的解时，请使用字符串加法，因为测试用例数字可能过大，会超过计算机的上限

解答

// 字符串加法，这里直接拷贝了网上现成的解答
var addition = function(num1, num2) {
let i = num1.length - 1, j = num2.length - 1, add = 0;
const ans = [];
while (i >= 0 || j >= 0 || add != 0) {
const x = i >= 0 ? num1.charAt(i) - '0' : 0;
const y = j >= 0 ? num2.charAt(j) - '0' : 0;
const result = x + y + add;
ans.push(result % 10);
add = Math.floor(result / 10);
i -= 1;
j -= 1;
}
return ans.reverse().join('');
}
var padZero = function (num) {
let zero = ''
while (num) {
zero += '0'
num -= 1
}
return zero
}
/**
* @param {string} num1
* @param {string} num2
* @return {string}
*/
var multiply = function(num1, num2) {
const divideAndConquer = (str1, str2) => {
let str1High, str1Low, str2High, str2Low, str1Carry, str2Carry, r1, r2, r3, r4
if (str1.length > 1) {
const str1MiddIndex = Math.floor(str1.length / 2)
str1High = str1.slice(0, str1MiddIndex)
str1Low = str1.slice(str1MiddIndex)
str1Carry = str1Low.length
} else {
str1High = str1
str1Low = '0'
str1Carry = 0
}
if (str2.length > 1) {
const str2MiddIndex = Math.floor(str2.length / 2)
str2High = str2.slice(0, str2MiddIndex)
str2Low = str2.slice(str2MiddIndex)
str2Carry = str2Low.length
} else {
str2High = str2
str2Low = '0'
str2Carry = 0
}
if (str1High.length <= 1 && str2High.length <= 1) {
r1 = String(Number(str1High) * Number(str2High)) + padZero(str1Carry + str2Carry)
} else {
r1 = divideAndConquer(str1High, str2High) + padZero(str1Carry + str2Carry)
}
if (str1High.length <= 1 && str2Low.length <= 1) {
r2 = String(Number(str1High) * Number(str2Low)) + padZero(str1Carry)
} else {
r2 = divideAndConquer(str1High, str2Low) + padZero(str1Carry)
}
if (str1Low.length <= 1 && str2High.length <= 1) {
r3 = String(Number(str1Low) * Number(str2High)) + padZero(str2Carry)
} else {
r3 = divideAndConquer(str1Low, str2High) + padZero(str2Carry)
}
if (str1Low.length <= 1 && str2Low.length <= 1) {
r4 = String(Number(str1Low) * Number(str2Low)) + ''
} else {
r4 = divideAndConquer(str1Low, str2Low)
}
return addition(addition(r1, r2), addition(r3, r4))
}
const result =  divideAndConquer(num1, num2)
if (result[0] === '0') {
return '0'
}
return result
};

后续

leetcode上一些分治题目的分析和解答，如有错误还请指正。应该可以对分治的思想有点浅薄的认知。共勉吧。

以上是 【JS】分而治之, 逐个击破 的全部内容， 来源链接： utcz.com/a/94858.html