A*算法求解15数码问题
目录
一、问题描述
二、算法简介
三、算法步骤
四、评估函数
五、参考资料
六、源代码(Java实现)
一、问题描述
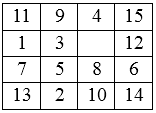
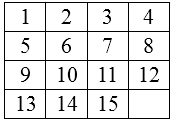
利用A*算法进行表1到表2的转换,要求空白块移动次数最少。
转换规则为:空白块只可以与上下左右四个方向的相邻数字交换。
表1 起始状态 表2 目标状态
二、算法简介
A*算法是一种在图形平面上,有多个节点的路径,求出最低通过成本的算法。该算法综合了Best-First Search和Dijkstra算法的优点:在进行启发式搜索提高算法效率的同时,基于评估函数计算损失,保证找到一条最优路径。
算法能否找到最优解的关键在于评估函数的选择,A*算法的评估函数表示为:f(n) = g(n) + h(n)
f(n) 是从初始状态经由状态n到目标状态的代价估计
g(n) 是在状态空间中从初始状态到状态n的实际代价
h(n) 是从状态n到目标状态的最佳路径的估计代价
例如在8数码问题中,g(n) 表示状态空间树中搜索的层数,h(n) 表示状态n与目标状态中元素位置不同的元素个数。
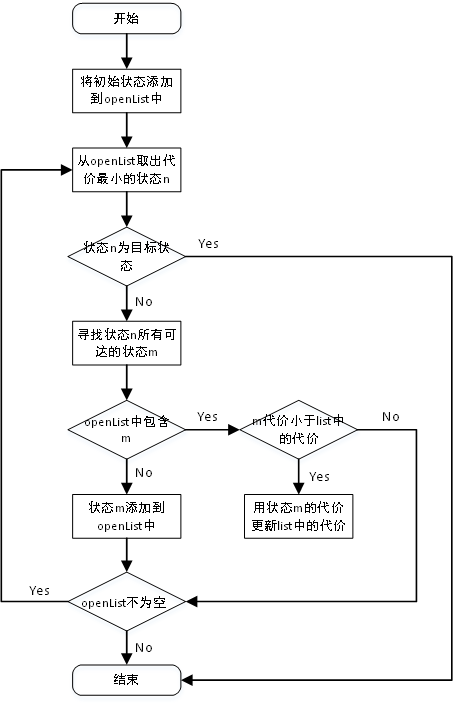
三、算法步骤
设定两个集合,open集,close集
1. 将起始点加入open集(设置父亲节点为空)
2. 在open集中选着一个f(n)值最小的节点作为当前节点
2.1 将当前节点从open集中移除,添加到close集
2.2 如果当前节点为终点节点,那么结束搜索
2.3 处理当前节点的所有邻接节点,规则如下:
如果不在open集中,那么就将其添加到open集,并将该节点的父节点为当前节点
如果已经添加到open集中,重新计算f(n)值,如果f(n)值小于先前的f(n)值,那么就更新open集中相应节点的f(n)
如果该节点不可通过或者已经被添加到close集,那么不予处理
3、如果open集不为空,那么转到步骤2继续执行。
四、评估函数
1. f(n) = 状态n状态空间树中的搜索深度 + 状态n与目标状态不同的元素个数
效果:与8数码问题使用了相同的评估函数,大概跑了30W步无法求出解
评价:效果极差,15数码问题的状态空间树要远复杂于8 数码问题,且15数码问题中空白块的移动更为复杂,此评估函数不适用。
2. f(n) = 状态n状态空间树中的搜索深度 + 状态n与目标状态各个位置数字偏差的绝对值
效果:随着搜索的进行,空白块的移动集中在表格上部,表格下部几乎不移动 ,无法求出解
评价:因为下部数字较大,移动后差值较大造成评估值较大,因此搜索集中在了数值较小的部分,效果很差。
3. f(n) = 状态n状态空间树中的搜索深度 + 状态n与目标状态各个元素的路径差值(一维数组各元素的距离差之和)
效果:空白块最终移动55步得到目标状态。
评价:效果比较理想,但h(n)还可继续优化。
4. f(n) = 状态n状态空间树中的搜索深度 + 状态n与目标状态各个元素的曼哈顿距离
效果:空白块最终移动41步得到目标状态。
评价:效果理想。
实际上,1和2的评估函数效果大致相同,都将搜索局限在了一部分导致无法计算出问题的解。3实际是以一维数组各元素的距离差之和估计状态n到目标状态的曼哈顿距离,但此估计方式和计算平面两点的曼哈顿距离存在较大误差,因此只求解出可行解。
五、参考资料
A*算法详解,看完后全懂了
启发式搜索浅谈,解决八数码问题
六、源代码(Java实现)
Github地址:A*算法求解15数码问题
以上是 A*算法求解15数码问题 的全部内容, 来源链接: utcz.com/a/53706.html