向量及矩阵在OpenGL中的应用
虽然我们在使用OpenGL的过程中运用过向量和矩阵,但是并不是说我们必须要懂得向量和矩阵的数学原理才能使用够使用OpenGL。就好比我们不需要知道汽车是怎么造出来的,也不需要发动机是怎么工作的,我们一样可以开汽车。但是如果我们对此有一定的了解,也可以帮助我们知道什么时候需要更换机油、什么时候该去保养汽车了。所以简单的了解一下向量和矩阵的知识还是有必要的。
向量
定义
简单一句话来概括就是:即有大小,又有方向的量,就叫向量。
比如下图3D坐标系中:
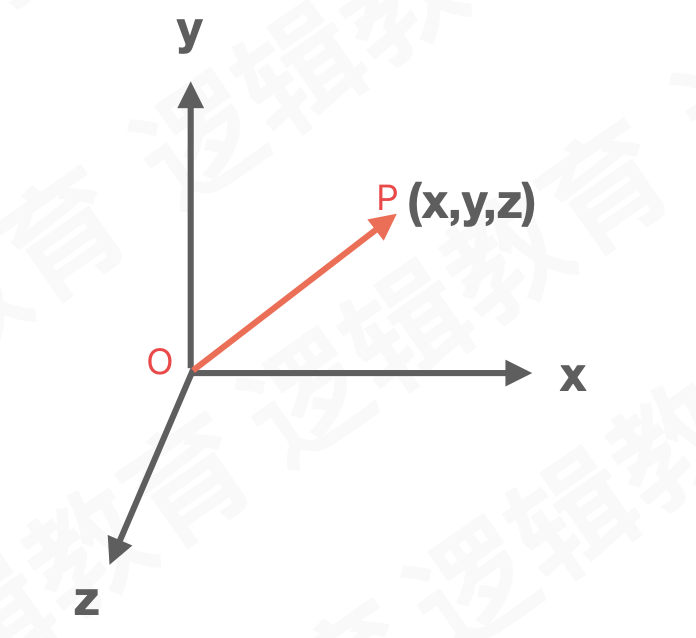
如上图,点O是坐标系的原点,点p的坐标是(x,y,z);由O指向P的线段长度是(x的平方+y的平方+z的平方)再开根号。OP即有长度,也有方向O指向P,称其为向量OP。
单位向量
向量长度我们称之为模,模为1的向量,我们称之为单位向量
单位化向量
将非单位向量转化为单位向量的过程标准化。
OpenGL如何定义向量【math3D库】
math3D库中有两个数据类型来定义三维向量和四维向量
- M3DVector3f 可以表示一个三维向量(x,y,z);
- M#Dvector4f 可以表示一个四维向量(x,y,z,w);一般情况下w设置为1,x,y,z通过除以w来进行缩放。
三维向量量/四维向量量的声明
typedef float M3DVector3f[3];typedef float M3DVector4f[4];
声明⼀一个三维向量量 M3DVector3f:类型 vVector:变量量名
M3DVector3f vVector;声明⼀一个四维向量量并初始化⼀一个四维向量量
M3DVector4f vVertex = {0,0,1,1};声明⼀一个三分量量顶点数组,例例如⽣生成⼀一个三⻆角形
M3DVector3f vVerts[] = {-0.5f,0.0f,0.0f, 0.5f,0.0f,0.0f, 0.0f,0.5f,0.0f
};
向量的“点乘”
向量可以进行 加法,减法计算. 但是向量里有⼀个在开发中使用价值非常⾼的操作,叫做
“点乘(dot product)” .点乘只能发⽣生在2个向量之间进行;
2个(三维向量)单元向量 之间进行点乘运算将得到⼀个标量(不不是三维向量,是⼀一个标量).
它表示两个向量之间的夹角;
前提条件: 2个向量必须为单位向量;
动作: 2个三维向量之间进⾏点乘
结构: 返回⼀一个[-1,1]范围的值. 这个值其实就是 夹角的cos值(余弦值)
如何单位化向量量?
(x/|xyz|, y/|xyz|, z/|xyz|); 使⽤⼀个⾮零向量除以它的模(向量的长度), 就可以得到⽅向相同的单位向量;
OpenGL提供了m3dDotProduct3 函数获得2个向量之间的点乘结果
float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v);m3dGetAngleBetweenVector3 即可获取2个向量量之间夹⻆的弧度值
float m3dGetAngleBetweenVector3(const M3DVector3f u,constM3DVector3f v);
向量的叉乘
向量之间的叉乘(cross product) 也是在业务开发里非常有⽤的⼀个计算方式; 2个向量 之间叉乘就可以得到另外⼀个向量,新的向量会与原来2个向量定义的平面垂直. 同时进行叉乘,不必为单位向量;
前提: 2个普通向量
动作: 向量与向量叉乘
结果: 向量(垂直于原来2个向量定义的平面的向量)
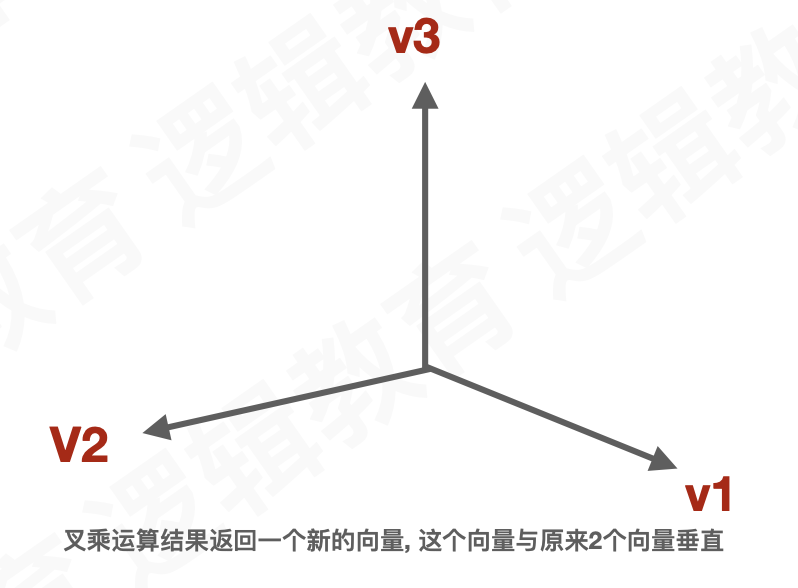
如上图,向量V1和向量V2的叉乘得到的结果向量V3,也称其为向量V1和向量V2的法向量.
openGL中使用m3dCrossProduct3函数获取两个向量叉乘的结果
void m3dCrossProduct3(M3DVector3f result,const M3DVector3f u ,constM3DVector3f v);
矩阵
定义
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:

这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
OpenGL中常用的矩阵
三维矩阵
typedef float M3DMatrix33f[9];四维矩阵
typedef float M3DMatrix44f[16];在其他编程标准中, 许多矩阵库定义一个矩阵时,使⽤⼆维数组;
OpenGL的约定里,更多倾向使用 一维数组; 这样做的原因是: OpenGL 使⽤的是 Column-Major(以列为主)矩阵排序的约定;
列优化的矩阵

行优化的矩阵

列优先的矩阵的奥秘之处在于16个值表示空间中一个特定的位置,这4列中,每一列都是4个元素组成的向量
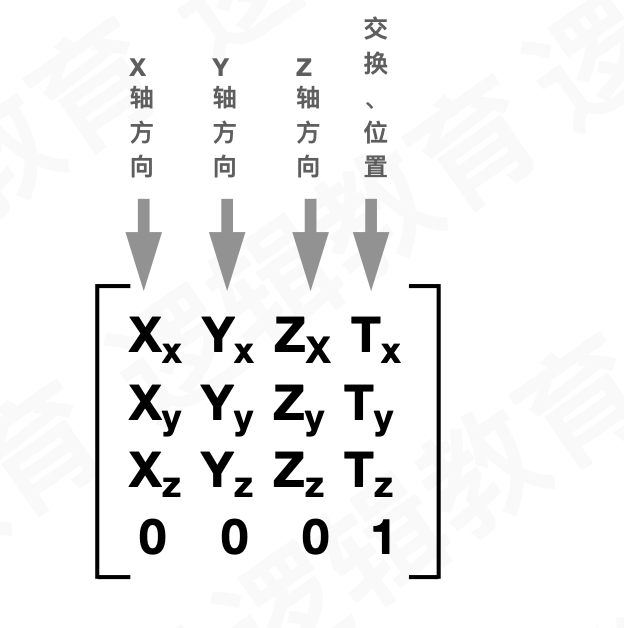
一个4*4矩阵是如何在3D空间中表示一个位置和⽅向的 列向量进行了特别的标注:矩阵的最后⼀行都为0,只有最后⼀个元素为1
如果将⼀个对象所有的顶点向量 乘以这个矩阵,就能让整个 对象变换到空间中给定的位置和⽅向上,如平移、旋转和缩放。
单元矩阵
对角线上的元素全部为1,其他元素全部为0的矩阵称之为单元矩阵

OpenGL中单元矩阵的定义
方式一
GLFloat m[] = {1,0,0,0,
0,1,0,0,
0,0,1,0,
0,0,0,1
};
方式二
M3DMatrix44f m[] = {1,0,0,0,
0,1,0,0,
0,0,1,0,
0,0,0,1
};
方式三
void m3dLoadIdentify44f(M3DMatrix44f m);矩阵的乘法
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵.
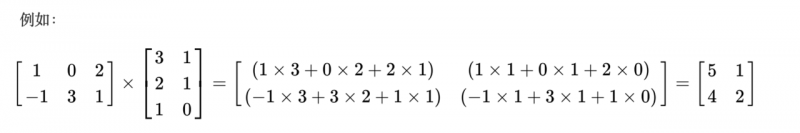
- 结合律: (AB)C = A(BC);
- 左分配律: (A+B)C = AC+BC;
- 右分配律: A(B+C) = AB+AC;
- 矩阵乘法不满足交换律。AB不等于BA
变换顶点向量 = 投影矩阵 ✖ 视图变换矩阵 ✖ 模型矩阵 ✖ 顶点

当一个图形发生平移、旋转和缩放时,其实是在平移、旋转和缩放图形上面的所有顶点。而我们可以通过设置投影矩阵、视图变换矩阵和模型矩阵与顶点向量进行相乘,从而将平移、旋转和缩放后的结果映射到顶点坐标上得到新的顶点坐标。

- 1.从栈顶获取栈顶矩阵,将栈顶矩阵与投影矩阵相乘,并将结果压入栈顶;
- 2.从栈顶获取栈顶矩阵,将栈顶矩阵与视图变换矩阵相乘,并将结果压入栈顶;
- 3.从栈顶获取栈顶矩阵,将栈顶矩阵与模型变换矩阵相乘,并将结果压入栈顶。
#理解在OpenGL里的变化
OpenGL常用的变换如下图:
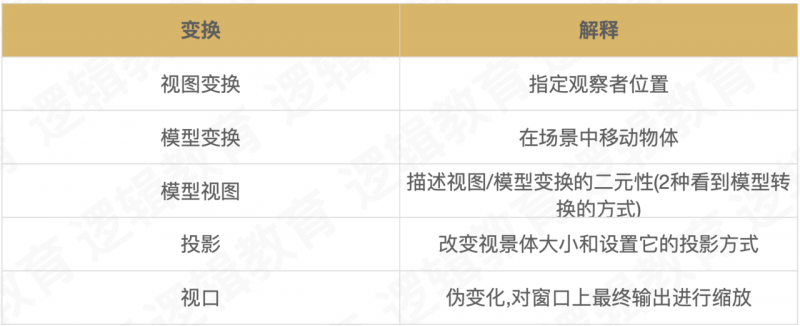
视图变换
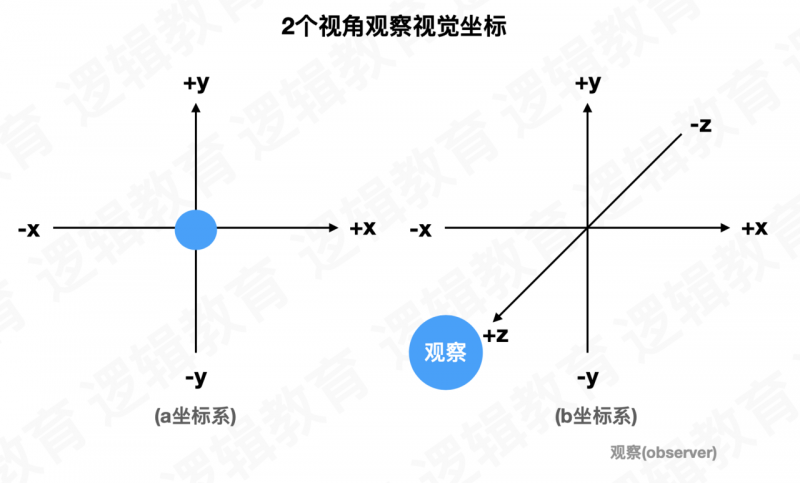
视图变换是应用到场景中的第一种变换, 它用来确定场景中的有利位置,在默认情况下, 透视
投影中位于原点(0,0,0),并沿着 z 轴负方向进行观察 (向显示器器内部”看过去”). 当观察者点位于原点(0,0,0) 时,就像在透视投影中一样.
视图变换将观察者放在你希望的任何位置.并允许在任何方向上观察场景, 确定视图变换就像在场景中放置观察者并让它指向某⼀个⽅向;
从⼤局上考虑, 在应用任何其他模型变换之前, 必须先应用视图变换. 这样做是因为, 对于视觉坐标系⽽言, 视图变换移动了当前的⼯作的坐标系; 后续的变化都会基于新调整的坐标系进行.
以上是 向量及矩阵在OpenGL中的应用 的全部内容, 来源链接: utcz.com/a/33150.html