数学建模 时间序列分析
概述
目的:预测未来
准备工作:描述过去、分析规律
常用的三种模型:季节分解、指数平滑方法、ARIMA模型
使用的软件:SPSS
时间序列=时间要素(年季度月)+数值要素(体重、GDP)
时间序列 :时期序列(连续变化,累计的过程)/时点序列(每过一段时间测一次)
时期序列可加,加起来反应的是发展的总量(GDP);时点序列不可加,加起来没有意义(体重)
灰色预测有一个累加的过程,所以灰色预测模型仅适用于时期序列
时间序列分解
概念
百度指数可以看舆论的趋势:index.baidu.com/v2/index.ht…


例子:



SPSS实际操作
STEP1:
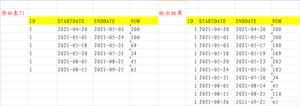
无效数据处理:
- 缺失值发生在时间序列的开头或者尾部,可采用直接删除的方法;
- 缺失值发生在序列的中间位置,则不能删除(删除后原有的时间序列会错位),
可采用替换缺失值的方法。

STEP2:
然后进行季节性分解(此题是加法模型):得到下面四个变量


STEP3:
对四个变量作图

若要预测则对T+C+L这条直线进行回归,拟合,得到的结果再加上季节性调整因子S就能得到正确预测结果
☆不能时间序列分解->使用专家建模器选择合适的模型

☆使用专家建模器
在考虑指数平滑法和ARIMA模型的基础上,自动查找序列的最佳拟合模型,还可以自动检测离群值
目标: 不完全能掌握指数平滑法和ARIMA模型;能够根据专家建模器得到的结果进行一些分析就行啦
指数平滑:simple模型

局限性:只能预测一期!

线性趋势模型(linear trend)

论文里就把这几个式子写上,介绍一下这几个参数的含义
阻尼趋势模型(Damped trend)


简单季节性(Simple seasonal)

温特加法模型(Winters' additive)

稳定的季节成分==加法,比较稳定
温特乘法模型(Winters' multiplicative)

不稳定的季节成分==乘法,波动较大,会趋向变大或变小
☆专家建模器操作过程
☆专家建模器结果分析
描述性回归与预测性回归
- 预测性回归不看显著性,只看预测误差
*描述性回归看显著性
十个知识点:

ARIMA模型
平稳时间序列和白噪声序列
协方差平稳/时间序列平稳性:

意义: 平稳性质比较好,均值方差都是常数,方便建模;若不平稳,则使用差分进行一定的变形就平稳了
白噪声序列=扰动项
例子:

- a:均值变大,不是个常数,不平稳
- c:方差变化,不是个常数,不平稳
- d:有季节趋势,方差不是个常数,不平稳
- e:下降趋势,均值变小,不平稳
- f:三个部分的均值不同,所以不平稳
- h:有季节趋势,方差不是个常数,不平稳
- i:上升趋势,不平稳
平稳的是:
- b:均值常数,方差常数,波动一致,有一个异常值可以忽略掉
- g:g有点怪怪的,不是很标准
差分方程

p:把时间序列滞后了p期
q:把扰动项滞后了q期
第一个和第二个加起来就是第三个自回归移动平均模型,即AR加上MA模型得到ARMA模型
z是其他变量,二元时间序列模型
红色字体部分是差分方程的其次部分
ARMA(p,q)模型:

p:把时间序列滞后了p期;q:把扰动项滞后了q期
做差分的意义: ARMA(p,q)模型特征方程的解的模长可以判断时间序列是否平稳
滞后算子

类似于微分算子
ARMA(p,q)模型用滞后算子表示:
不平稳转换为平稳:用差分
AR(p)模型==p阶自回归模型

一般进行回归的时候,要先对扰动项进行自相关检查,看他是不是独立同分布iid,即是不是自相关==前一项和后一项有关系;引入自回归就可以自相关的情况
重要事项:我们讨论的AR(p)模型一定
是平稳的时间序列模型,
如果原数据不平稳也要先
转换为平稳的数据才能再
进行建模。
特征方程判断平稳+不平稳转换为平稳过程

k->∞,爆炸
例子:

MA(q)模型==q阶移动平均模型

MA模型和AR模型的关系:

意义: AR很多参数,转化为MA模型后参数就变少了,更容易分析
证明MA(q)的平稳性:一般都是平稳的

☆ARMA(p,q)模型
自回归移动平均模型(Autoregressive Moving Average,ARMA),

ARMA(p,q)模型的平稳性
MA(q)必定平稳,只判断AR(q)即可

用stata软件方便进行单位根检验(假设检验)
(软件生成结果)判断ARMA阶数:ACF自相关系数,PACF偏自相关函数


自相关系数=间隔s期的协方差除以各自的标准差
间隔s为自变量的函数=自相关函数
白噪声 γs=0
通过求回归系数求出自相关系数
☆例子:通过两个图判断阶数





ARMA(p,q)两个图都是拖尾的,故难以判断,spss软件会告诉我们正确阶数!,如下图:

ARMA模型的估计
ARMA模型的极大似然估计
建模后求系数,用极大似然估计;用软件自动进行!
模型选择:AIC和BIC准则(选小原则)

pq设置越大,自变量越多,拟合越好,不过会存在过拟合问题,所以要通过AIC和BIC准则进行一个权衡:模型选择要在模型复杂度与模型对数据的解释能力之间寻求最佳平衡。
模型中参数的个数越小越好,模型的极大似然函数值越大越好,所以AIC和BIC越小越好
n个时期=n个参数个数
BIC选择的模型更简洁
意义: 若有十个模型,求出他们的BIC/AIC进行比较,选择最小的那个
检查残差是不是白噪声

如果残差是白噪声,则说明我们选取的模型能完全识别出时间序列数据的规律,即模型可接受;如果残差不是白噪声,则说明还有部分信息没有被模型所识别,我们需要修正模型来识别这一部分的信息。----->使用Q检验
原假设:自相关系数都是0=它是白噪声序列
构造统计量Q,对其进行假设检验,软件会给出p值,直接判断就行
☆ARIMA(p,d,q)模型:差分自回归移动平均模型


例子:


☆SARIMA(Seasonal ARIMA)模型:考虑季节性调整因子

☆☆☆SPSS实操
Spss时间序列建模的思路:

对结果进行一些分析,解释:
如温特斯加法模型:



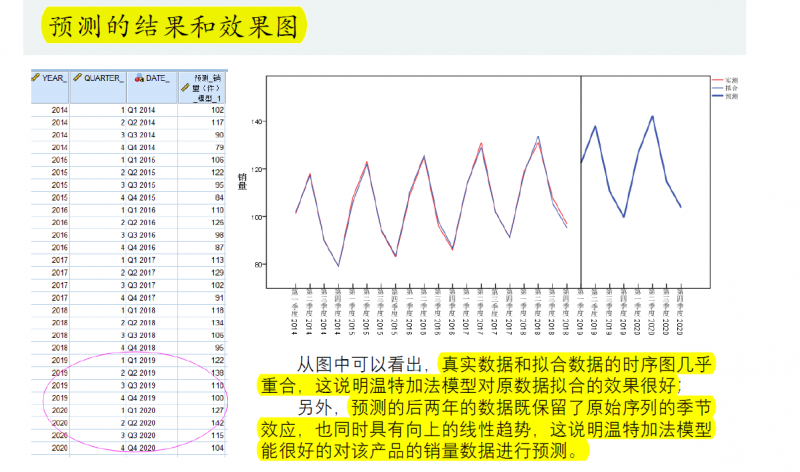
【注意】
人口预测不准确,他会一直呈上升趋势
例题3:上证指数预测
简单模型
Q检验里p=0,所以残差不是白噪声,所以这个模型不好;原因:有异常值,故剔除异常值后再建立模型
解决异常值后,是ARIMA(0,1,1.4)模型,模型得到了改善Q检验p>0.05,残差是白噪声,故模型ok
且简单模型只能预测一期
ARIMA(0,1,1.4)只能预测14期,♥解决办法:把得到的14期加上之前的数据再扔进去进行预测
例题4:GDP增速预测
真正的预测要结合背景,而不是直接套用模型
用所有数据进行预测(剔除异常值)----->拟合和预测的效果很差;原因:没有结合背景,14年后就取消了GDP考核
预测两要:
- 一要结合背景;
- 二要合理假设。
预测两不要:
- 不要硬套模型;
- 不要不做解释。
以上是 数学建模 时间序列分析 的全部内容, 来源链接: utcz.com/a/27355.html