算法导论一课时记录之算法分析
前言
算法分析是理论研究,是关于计算机程序性能和资源的利用研究,重点在于性能
对于程序设计来说,比性能更加重要的是正确性,简洁,可维护性,健壮性,但是性能的好坏直接决定可行与不可行,例如对于实时的要求,所以算法总是在最前沿
排序问题
插入排序
输入一组序列a1,a2直到an,按照要求重新排序之后输出,排序之后每一个数字出现仅出现一次,且a按升序排例,假如我们使用插入排序来完成
INSERTION-SORT(A)for j=1 to A.length:
key=A[j]
//将A[j]插入已排序序列A[1..j-1]
i=j-1
while i>0 and A[i]>key
A[i+1]= A[i]
i=i-1
A[i+1]=key
STEP1: 声明一个数组A
STEP2:设置外部循环条件从j=2开始递增,内部循环条件i=j-1递减直到i==0,循环的作用在于完成增量,使得每一次排序过后的数组长度+1
STEP3:用没有排序过的数组的第一项依次和已经排序过的数组比较
package com.tan.sort;/**
*
* @author 谭婧杰
*
*/
public class InsertSort {
public static void main(String[] args) {
int[] A = {5,2,4,6,1,3};
for(int i = 1;i <A.length;i++) {
for(int j = i;j >0;j--) {
if(A[j-1] >A[j]) {
int temp = A[j-1];
A[j-1] = A[j];
A[j] = temp;
}
}
}
}
}
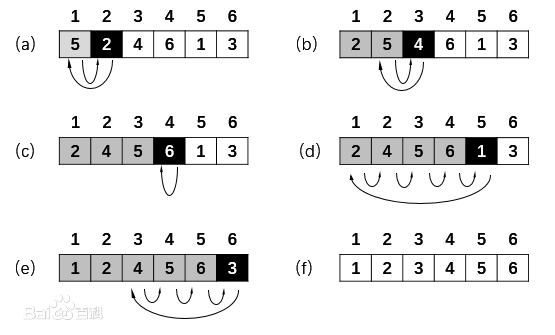
// -> 1 2 3 4 5 6
| 5 | 2 | 4 | 6 | 1 | 3 |
|---|---|---|---|---|---|
| 2 | 5 | 4 | 6 | 1 | 3 |
| 2 | 4 | 5 | 6 | 1 | 3 |
| 2 | 4 | 5 | 1 | 6 | 3 |
| 2 | 4 | 1 | 5 | 6 | 3 |
| ..... | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
运行时间
运行时间取决于多种因素
输入本身
- 最优情况:输入已经有序
- 最坏情况:输入逆序
运算规模
处理的输入规模越大,运行时间越长,通常处理输入规模的方式是依输入规模将其参数化,运行时间的上界代表着对于用户的承诺
分析
- 最坏情况分析:T(n)定义为输入规模为n时的最长运行时间
- 最好情况分析:
- 平均情况:T(n)定义为输入规模为n时所有可能输入的期望值(加权平均)
渐近分析
忽略掉依赖机器的常量,不去检查实际运行时间而是关注运行时间的增长
Θ
对于一个公式,丢弃它的低阶项,并忽略它的常数因子
EX:3n^3+90*n^2-8n+567 = Θ(n^3)
假如我们关注一个n倾向于无穷大时候,就会意识到Θ(n^2)迟早会战胜Θ(n^4),对于小的n来说,插入排序是快的,但是对于一个巨大的n来说,插入排序就显得不那么快了,所以有另一个更快的排序算法,归并排序
归并排序
对于数组A[1...n]的归并排序,存在三个基本步骤:
STEP1:if n = 1; done
STEP2:否则递归对A[1到n/2向上取整]以及A[n/2+1向上取整..n]这部分排序
STEP3:排序之后的两个表归并
归并排序为线性时间的Θ(n)b
以上是 算法导论一课时记录之算法分析 的全部内容, 来源链接: utcz.com/a/24948.html