【Java】B-Tree 和 B+Tree傻傻分不清楚
B-Tree 和 B+Tree傻傻分不清楚
李小二发布于 2 月 1 日
B-Tree
B-Tree又叫做B树,和平衡二叉树不同的地方在于B树是多叉树(平衡多路查找树),Oracle和MongoDB的索引技术就是基于B树的数据结构,B树也可以看作是对2-3查找树的一种扩展。
一个m阶的B-Tree有以下性质
- 每个节点最多有m个子节点;
- 每个非叶子节点(根节点除外)至少含有m/2个子节点;
- 如果根节点不是叶子节点,那么根节点至少有两个子节点;
- 每个节点上,所有的关键字都是有序的,从左到右,依次从小到大排序;
- 每个关键字的左子树的均值小于当前关键字,右子树的均值大于当前关键字;
- 每个节点都存有索引和数据;
- 对于一个非叶子节点而言,它最多能存储m-1个关键字;
- 所有叶子节点位于同一层。
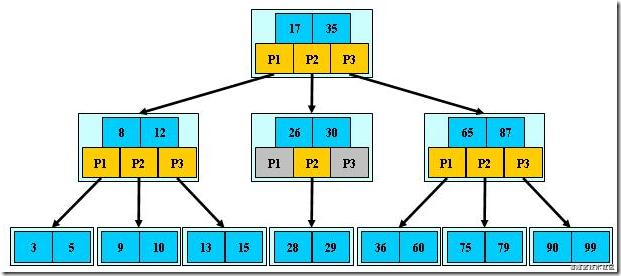
B树查找
我们以查找13为例子:
第一次磁盘IO:定位到比17小,选择最左子树;
第二次磁盘IO:定位到比12大,选择最右子树;
第三次磁盘IO:定位到13,查出对应的数据后,查找结束。
B树插入
对于一个m阶B树,新节点一般是插在叶子层,但是需要根据实际的情况考虑是否需要裂变。
1.若该节点中关键码个数小于m-1,则直接插入;
2.若该节点中关键字个数等于m-1,则将进行分裂,以中间关键字为界点将节点一分为2,产生一个新的节点,并把中间那个关键字插入到父节点中,继续判断父节点的关键字个数是否等于m-1,依次判断是否分裂,最坏情况下可一直分裂到根节点,整个树增加一层。
B树删除
B树的删除也非常复杂
如果关键字所在节点的原关键树>=(m/2),说明删除后仍可满足B树的结构,可以直接干掉。
如果被删除后不再满足B树的结构,则需要一定的调整过程:
如果其左右兄弟节点中有多余的关键字,即与该节点相邻的节点中关键字的数目大于(m/2)-1,就会将兄弟节点中的最大(左兄弟)或者最小(右兄弟)移到夫节点上,然后将双亲节点中小于(右兄弟的上移)或者大于(左节点上移)关键字的关键字下移到被删关键字的节点中。
如果其左右兄弟都没有多余关键字的时候,情况将变得非常非常复杂;需把删除关键字节点与其左(或者右)兄弟节点中的关键字合并到(父节点指向该删除关键字节点的左(右)兄弟节点的指针)所指向的兄弟节点中去,如果因此父节点中的关键字个数小于规定值,则需要对父节点做同样的处理,最坏情况下会使得整个树减少一层。
总结
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘块大小范围;把树的节点关键字增多后树的层级比原来的二叉树少了很多,大大减少了数据查找和比较的次数,提高了效率。
B+树
B+Tree中如果有N个关键字则会拥有n个分支,而B树中n个关键字的节点包含n+1个分支。
B+Tree中,每个非根节点中的关键字个数是>=(m/2)且<=m,而B树是>=(m/2)-1且<=(m-1)。
B+Tree中根节点的关键字个数是>=1且<=m,而B树是>=1且<=(m-1)。
B+树是B树的一个升级版,因为B+Tree非叶子节点不存储关键字记录的指针,所以其相对于B树来说B+树更充分的利用了节点的空间,让查找速度更加稳定,其速度完全接近于二分查找。
1. B+树的非叶子节点不对关键字记录的指针进行保存,只进行数据索引,使得B+树非叶子节点能保存关键字的能力大大提升,而且树的层级会更少;
2.B+树叶子节点保存了其父节点的关键字记录的指针,所以每次查询必须到叶子节点才能真正获取到相关数据,而且平很多叉树的特点是所有子节点的层级相差不会超过一,所以查询速度相对是非常稳定的;
3.B+Tree树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针;
4.非叶子节点的子节点树=关键字数。
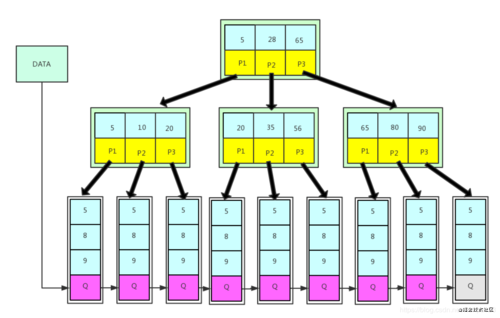
B+树查找
B+树的查找规格是B树一样,都是按照大小一层一层往下,但是不同点在于其一定会执行到叶子节点,因为只有叶子节点才会存储数据的指针。
B+树插入
插入操作全部在叶子节点中进行
1.若为空树,创建一个叶子节点,然后将记录插入,同时这个叶子节点也是根节点;
2.若被插入的关键字所在的节点,其含有的关键字数目小于m,则直接插入;
3.若被插入关键字所在的节点的关键字数等于m的时候,则需要分裂为两个节点,并将m/2的关键字上移到父节点中,同时判断父节点的关键字个数是否大于m,如果需要分裂继续按照上面的流程进行分裂。
B+树删除
1.如果要删除关键字所在节点的关键字个数,如果大于m/2,直接删除即可;
2.当删除关键字所在节点的关键字个数等于m/2的时候,若兄弟节点中含有多余的关键字,也可从兄弟节点中借用关键字完成删除操作;
3.若兄弟节点没有多余的关键字,则需要与其他兄弟进行合并;
4.如果合并后导致父节点不再符合B+树的结构,则需要按照上面的规律进行再次结构的调整;
5.注意B+树的结构(非叶子节点会存储索引信息,叶子节点才会存储数据指针),修改完后还需修改其父节点中的索引值。
总结
1. B+树的层级更少;
2. B+树查询速度更加稳定;
3.B+树天然具备排序功能,由于B+树所有的叶子节点数据构成了一个有序链表,在查询范围区间数据的时候会更加方便,数据紧密性很好高;
4.B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,而B树需要对每一层进行遍历,所以B+树更有利于全表扫描;
B*树
B*树是B+树的变种,不同点如下
1.关键字个数限制,B+树初始化的关键字的个数是m/2,而B树的初始化个数是2m/3,所以B树的层级会更少;
2.B+树节点满时就会分裂,而B*树满时会检查兄弟节点是否满,如果兄弟节点没有满的话则会向兄弟节点转移关键字,如果兄弟节点也满了的话则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来。这个特性使得其相对B+树分裂的次数也更少;
3.B*树除了根节点外的非叶子节点也会存储兄弟节点的指针;
总结
B*树对比 B+Tree其初始化的容量更大,存储的关键字更多,层级更少,裂变次数也会更少。
阅读 11发布于 2 月 1 日
本作品系原创,采用《署名-非商业性使用-禁止演绎 4.0 国际》许可协议
李小二
解决别人生产的Bug,给别人生产Bug
46 声望
3 粉丝
李小二
解决别人生产的Bug,给别人生产Bug
46 声望
3 粉丝
宣传栏
目录
B-Tree
B-Tree又叫做B树,和平衡二叉树不同的地方在于B树是多叉树(平衡多路查找树),Oracle和MongoDB的索引技术就是基于B树的数据结构,B树也可以看作是对2-3查找树的一种扩展。
一个m阶的B-Tree有以下性质
- 每个节点最多有m个子节点;
- 每个非叶子节点(根节点除外)至少含有m/2个子节点;
- 如果根节点不是叶子节点,那么根节点至少有两个子节点;
- 每个节点上,所有的关键字都是有序的,从左到右,依次从小到大排序;
- 每个关键字的左子树的均值小于当前关键字,右子树的均值大于当前关键字;
- 每个节点都存有索引和数据;
- 对于一个非叶子节点而言,它最多能存储m-1个关键字;
- 所有叶子节点位于同一层。

B树查找
我们以查找13为例子:
第一次磁盘IO:定位到比17小,选择最左子树;
第二次磁盘IO:定位到比12大,选择最右子树;
第三次磁盘IO:定位到13,查出对应的数据后,查找结束。
B树插入
对于一个m阶B树,新节点一般是插在叶子层,但是需要根据实际的情况考虑是否需要裂变。
1.若该节点中关键码个数小于m-1,则直接插入;
2.若该节点中关键字个数等于m-1,则将进行分裂,以中间关键字为界点将节点一分为2,产生一个新的节点,并把中间那个关键字插入到父节点中,继续判断父节点的关键字个数是否等于m-1,依次判断是否分裂,最坏情况下可一直分裂到根节点,整个树增加一层。
B树删除
B树的删除也非常复杂
如果关键字所在节点的原关键树>=(m/2),说明删除后仍可满足B树的结构,可以直接干掉。
如果被删除后不再满足B树的结构,则需要一定的调整过程:
如果其左右兄弟节点中有多余的关键字,即与该节点相邻的节点中关键字的数目大于(m/2)-1,就会将兄弟节点中的最大(左兄弟)或者最小(右兄弟)移到夫节点上,然后将双亲节点中小于(右兄弟的上移)或者大于(左节点上移)关键字的关键字下移到被删关键字的节点中。
如果其左右兄弟都没有多余关键字的时候,情况将变得非常非常复杂;需把删除关键字节点与其左(或者右)兄弟节点中的关键字合并到(父节点指向该删除关键字节点的左(右)兄弟节点的指针)所指向的兄弟节点中去,如果因此父节点中的关键字个数小于规定值,则需要对父节点做同样的处理,最坏情况下会使得整个树减少一层。
总结
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘块大小范围;把树的节点关键字增多后树的层级比原来的二叉树少了很多,大大减少了数据查找和比较的次数,提高了效率。
B+树
B+Tree中如果有N个关键字则会拥有n个分支,而B树中n个关键字的节点包含n+1个分支。
B+Tree中,每个非根节点中的关键字个数是>=(m/2)且<=m,而B树是>=(m/2)-1且<=(m-1)。
B+Tree中根节点的关键字个数是>=1且<=m,而B树是>=1且<=(m-1)。
B+树是B树的一个升级版,因为B+Tree非叶子节点不存储关键字记录的指针,所以其相对于B树来说B+树更充分的利用了节点的空间,让查找速度更加稳定,其速度完全接近于二分查找。
1. B+树的非叶子节点不对关键字记录的指针进行保存,只进行数据索引,使得B+树非叶子节点能保存关键字的能力大大提升,而且树的层级会更少;
2.B+树叶子节点保存了其父节点的关键字记录的指针,所以每次查询必须到叶子节点才能真正获取到相关数据,而且平很多叉树的特点是所有子节点的层级相差不会超过一,所以查询速度相对是非常稳定的;
3.B+Tree树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针;
4.非叶子节点的子节点树=关键字数。

B+树查找
B+树的查找规格是B树一样,都是按照大小一层一层往下,但是不同点在于其一定会执行到叶子节点,因为只有叶子节点才会存储数据的指针。
B+树插入
插入操作全部在叶子节点中进行
1.若为空树,创建一个叶子节点,然后将记录插入,同时这个叶子节点也是根节点;
2.若被插入的关键字所在的节点,其含有的关键字数目小于m,则直接插入;
3.若被插入关键字所在的节点的关键字数等于m的时候,则需要分裂为两个节点,并将m/2的关键字上移到父节点中,同时判断父节点的关键字个数是否大于m,如果需要分裂继续按照上面的流程进行分裂。
B+树删除
1.如果要删除关键字所在节点的关键字个数,如果大于m/2,直接删除即可;
2.当删除关键字所在节点的关键字个数等于m/2的时候,若兄弟节点中含有多余的关键字,也可从兄弟节点中借用关键字完成删除操作;
3.若兄弟节点没有多余的关键字,则需要与其他兄弟进行合并;
4.如果合并后导致父节点不再符合B+树的结构,则需要按照上面的规律进行再次结构的调整;
5.注意B+树的结构(非叶子节点会存储索引信息,叶子节点才会存储数据指针),修改完后还需修改其父节点中的索引值。
总结
1. B+树的层级更少;
2. B+树查询速度更加稳定;
3.B+树天然具备排序功能,由于B+树所有的叶子节点数据构成了一个有序链表,在查询范围区间数据的时候会更加方便,数据紧密性很好高;
4.B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,而B树需要对每一层进行遍历,所以B+树更有利于全表扫描;
B*树
B*树是B+树的变种,不同点如下
1.关键字个数限制,B+树初始化的关键字的个数是m/2,而B树的初始化个数是2m/3,所以B树的层级会更少;
2.B+树节点满时就会分裂,而B*树满时会检查兄弟节点是否满,如果兄弟节点没有满的话则会向兄弟节点转移关键字,如果兄弟节点也满了的话则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来。这个特性使得其相对B+树分裂的次数也更少;
3.B*树除了根节点外的非叶子节点也会存储兄弟节点的指针;
总结
B*树对比 B+Tree其初始化的容量更大,存储的关键字更多,层级更少,裂变次数也会更少。
以上是 【Java】B-Tree 和 B+Tree傻傻分不清楚 的全部内容, 来源链接: utcz.com/a/111828.html




得票时间