【Python】统计科学之聊聊你知道和不知道的相关性系数
统计科学之聊聊你知道和不知道的相关性系数
张俊红发布于 今天 06:58
01
这一篇我们来聊聊大家平常比较常用的相关系数。相关系数是用来度量两个变量之间相关性大小的一个量化指标。比如你要判断啤酒和尿布之间是否有相关性,就可以计算这两个变量的相关系数,通过相关系数来判断两者的相关性大小。相关系数主要有三种:Pearson相关系数、Spearman秩相关系数和Kendall τ相关系数。皮尔逊(Pearson)相关系数大家应该都知道,也应该有用到过。但是秩相关(Spearman)系数和τ相关(Kendall)系数大家或许不知道。我们这一篇就来聊聊这三个系数。
02
第一个讲的是大家熟悉的皮尔逊相关系数,在讲皮尔逊相关系数前,我们先讲一下另外一个概念,协方差。协方差是用来表示两个变量总体的误差,而方差是用来只表示一个变量的误差。协方差的公式如下: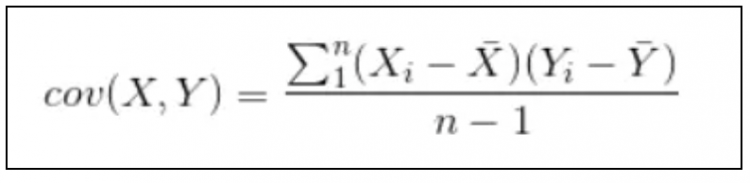
协方差除了表示两个变量总体的误差以外还用来表示两个变量之间的相关性,为什么协方差可以表示两个变量之间的相关性呢?我们需要从协方差的公式入手。通过上面公式中我们可以看出,协方差等于两个变量各自与均值之差的乘积和。
如果变量X与其均值的大小关系与变量Y完全一致,即变量X和Y的值要么同时大于均值要么同时小于均值,那这个时候得到的协方差全为正数,且协方差值达到最大;如果变量X与其均值的大小关系与变量Y刚好相反,即变量X大于其均值的时候变量Y刚好小于其均值,这个时候得到的协方差全为负数,且协方差值达到最小;如果变量X与其均值的大小关系与Y变量Y值部分一致,两者的乘积会有正有负,这个时候得到的协方差值就是介于最大值和最小值之间。X和Y变量的三种情况如下图所示: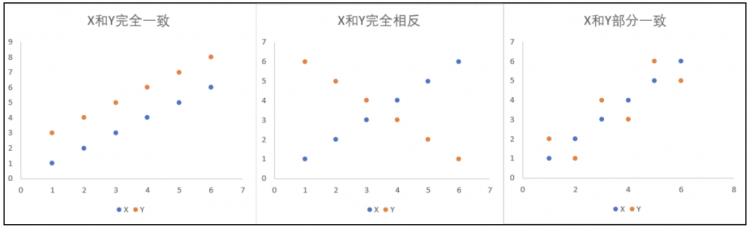
协方差比较容易受到量纲的影响,什么是量纲呢,就是单位,比如年龄和身高就不是一个单位,当X和Y变量的量纲之间的差别很大时,就会对协方差结果产生很大影响。下图中,左右两边的X和Y的趋势基本都一致,但是因为量纲不同(看纵坐标值),所以最后算出来的协方差会相差很大。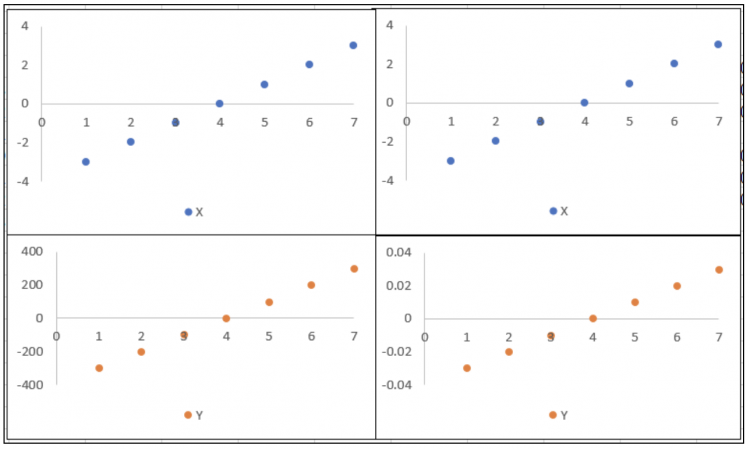
下表为上图中用到的数据集,感兴趣的同学可以根据公式自己计算下: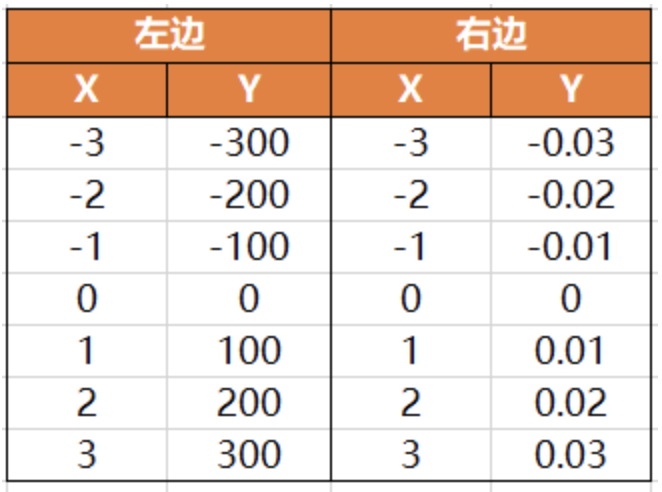
那对于上面这种不同量纲的影响我们该怎么办呢?明明趋势一致,但是算出来的协方差值会相差很大。什么原因导致的,我们就用什么方法解决。协方差差别很大的原因主要是因为量纲不同的原因引起的,那我们针对变量进行去量纲处理就行,怎么去量纲呢?就是在协方差的基础上再除以各自变量的标准差,这样就可以消除不同量纲的影响,具体公式如下: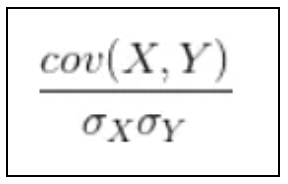
上面这个公式就是相关系数的公式,也就是我们常用的皮尔逊相关系数,这个系数的取值在[-1,1]之间,当值大于0说明两个变量是正相关,且值越接近于1,相关程度越强;当值小于0说明两个变量是负相关,且值越接近于-1,相关程度越强。
协方差不仅会受量纲的影响,还会受到异常值的影响,如果有异常值会拉高或拉低平均值,导致最后算出来的结果会有偏差。
03
讲完了皮尔逊相关系数,我们再来看看秩相关(Spearman)系数。
我们前面讲过皮尔逊系数容易受到异常值的的影响,过高和过低的值都会导致最后的结果有偏差,那有没有一种方法可以避免这种情况呢?答案就是我们这节要讲的秩相关(Spearman)系数,为什么这个可以避免异常值的影响呢?是因为这种方法没有使用变量的绝对值,而是使用了变量中绝对值出现的顺序,顺序就是将所有的变量值从小到大进行排序编号就行,是不是很有效。秩相关(Spearman)系数的公式如下: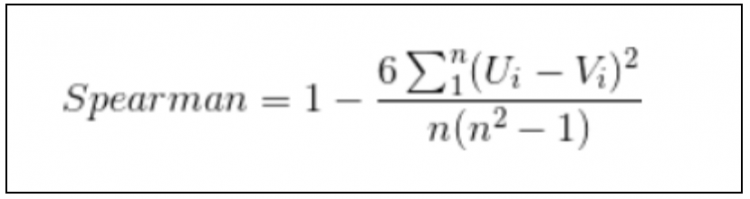
04
秩相关(Spearman)系数是用变量里面各值对应的顺序来代替原变量值的,还有另外一种类似的秩相关系数,叫做 Kendall τ秩相关系数。这种相关系数的方法也是利用变量值出现的顺序,但是与Spearman相关系数略有不同。具体求取方法为:先将变量X进行升序排列,然后再对变量Y从第一个开始,依次往后进行两两比较,最后看随着X的增大变量Y增大的值有多少,降低的有多少,通过增大的个数和降低的个数的比较来判定两个变量的相关性。
如下图所示,当我们对变量X进行升序排列以后,我们对变量Y从第一个值开始进行两两比较,一共需要比较的组合有:(1,3)、(1,6)、(1,2)、(1,5)、(1,4)、(3,6)、(3,2)、(3,5)、(3,4)、(6,2)、(6,5)、(6,4)、(2,5)、(2,4)、(5,4),然后我们看这里面大于的组合有多少,小于的组合有多少。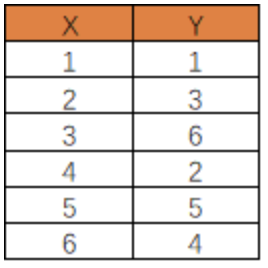
如果随着X的增大变量Y增大的值越多,降低的值越少,说明两个变量之间越正相关;如果随着X的增大变量Y增大的值越少,降低的值越多,说明两个变量之间越负相关;如果随着X的增大变量Y增大的值与降低的值的数量比较接近,说明两个变量之间相关性比较弱。
05
以上就是关于三种不同相关系数的一个简单介绍,平常大家应该对第一种皮尔逊相关系数了解比较多,但是严格意义上后两种要比第一种更加通用,而且适用场景更多一些,尤其是对异常值的影响。
当然了,我们在使用这些方法的过程中肯定是不需要去自己手动计算的,大家只需要明白其中的原理即可。这些相关性系数的求取在Python中都是有现成的函数供大家使用。df.corr()大家应该有人使用过,不知道你有没有看过这个函数里面的参数,这个函数里面有一个method参数,该参数有三个值可选:‘pearson’, spearman’,‘kendall’,分别对应我们上面的三种系数的求取。
本文就讲到这里,大家可以去使用起来啦。
python数据库网页爬虫自然语言处理深度学习
阅读 35发布于 今天 06:58
本作品系原创,采用《署名-非商业性使用-禁止演绎 4.0 国际》许可协议
张俊红
公众号:《俊红的数据分析之路》,分享数据分析相关的内容。
1 声望
0 粉丝
张俊红
公众号:《俊红的数据分析之路》,分享数据分析相关的内容。
1 声望
0 粉丝
宣传栏
01
这一篇我们来聊聊大家平常比较常用的相关系数。相关系数是用来度量两个变量之间相关性大小的一个量化指标。比如你要判断啤酒和尿布之间是否有相关性,就可以计算这两个变量的相关系数,通过相关系数来判断两者的相关性大小。相关系数主要有三种:Pearson相关系数、Spearman秩相关系数和Kendall τ相关系数。皮尔逊(Pearson)相关系数大家应该都知道,也应该有用到过。但是秩相关(Spearman)系数和τ相关(Kendall)系数大家或许不知道。我们这一篇就来聊聊这三个系数。
02
第一个讲的是大家熟悉的皮尔逊相关系数,在讲皮尔逊相关系数前,我们先讲一下另外一个概念,协方差。协方差是用来表示两个变量总体的误差,而方差是用来只表示一个变量的误差。协方差的公式如下: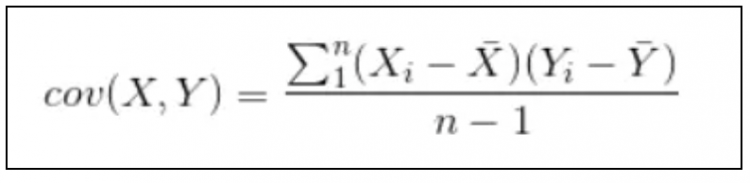
协方差除了表示两个变量总体的误差以外还用来表示两个变量之间的相关性,为什么协方差可以表示两个变量之间的相关性呢?我们需要从协方差的公式入手。通过上面公式中我们可以看出,协方差等于两个变量各自与均值之差的乘积和。
如果变量X与其均值的大小关系与变量Y完全一致,即变量X和Y的值要么同时大于均值要么同时小于均值,那这个时候得到的协方差全为正数,且协方差值达到最大;如果变量X与其均值的大小关系与变量Y刚好相反,即变量X大于其均值的时候变量Y刚好小于其均值,这个时候得到的协方差全为负数,且协方差值达到最小;如果变量X与其均值的大小关系与Y变量Y值部分一致,两者的乘积会有正有负,这个时候得到的协方差值就是介于最大值和最小值之间。X和Y变量的三种情况如下图所示:
协方差比较容易受到量纲的影响,什么是量纲呢,就是单位,比如年龄和身高就不是一个单位,当X和Y变量的量纲之间的差别很大时,就会对协方差结果产生很大影响。下图中,左右两边的X和Y的趋势基本都一致,但是因为量纲不同(看纵坐标值),所以最后算出来的协方差会相差很大。
下表为上图中用到的数据集,感兴趣的同学可以根据公式自己计算下:
那对于上面这种不同量纲的影响我们该怎么办呢?明明趋势一致,但是算出来的协方差值会相差很大。什么原因导致的,我们就用什么方法解决。协方差差别很大的原因主要是因为量纲不同的原因引起的,那我们针对变量进行去量纲处理就行,怎么去量纲呢?就是在协方差的基础上再除以各自变量的标准差,这样就可以消除不同量纲的影响,具体公式如下: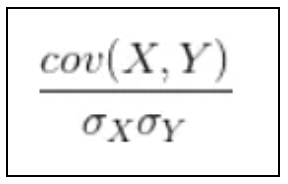
上面这个公式就是相关系数的公式,也就是我们常用的皮尔逊相关系数,这个系数的取值在[-1,1]之间,当值大于0说明两个变量是正相关,且值越接近于1,相关程度越强;当值小于0说明两个变量是负相关,且值越接近于-1,相关程度越强。
协方差不仅会受量纲的影响,还会受到异常值的影响,如果有异常值会拉高或拉低平均值,导致最后算出来的结果会有偏差。
03
讲完了皮尔逊相关系数,我们再来看看秩相关(Spearman)系数。
我们前面讲过皮尔逊系数容易受到异常值的的影响,过高和过低的值都会导致最后的结果有偏差,那有没有一种方法可以避免这种情况呢?答案就是我们这节要讲的秩相关(Spearman)系数,为什么这个可以避免异常值的影响呢?是因为这种方法没有使用变量的绝对值,而是使用了变量中绝对值出现的顺序,顺序就是将所有的变量值从小到大进行排序编号就行,是不是很有效。秩相关(Spearman)系数的公式如下: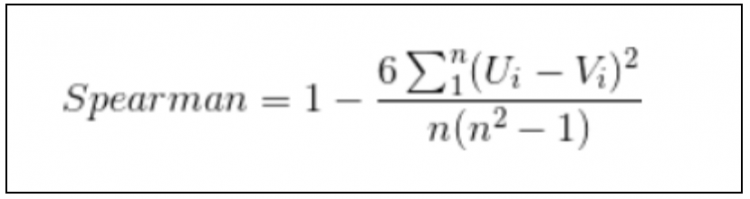
04
秩相关(Spearman)系数是用变量里面各值对应的顺序来代替原变量值的,还有另外一种类似的秩相关系数,叫做 Kendall τ秩相关系数。这种相关系数的方法也是利用变量值出现的顺序,但是与Spearman相关系数略有不同。具体求取方法为:先将变量X进行升序排列,然后再对变量Y从第一个开始,依次往后进行两两比较,最后看随着X的增大变量Y增大的值有多少,降低的有多少,通过增大的个数和降低的个数的比较来判定两个变量的相关性。
如下图所示,当我们对变量X进行升序排列以后,我们对变量Y从第一个值开始进行两两比较,一共需要比较的组合有:(1,3)、(1,6)、(1,2)、(1,5)、(1,4)、(3,6)、(3,2)、(3,5)、(3,4)、(6,2)、(6,5)、(6,4)、(2,5)、(2,4)、(5,4),然后我们看这里面大于的组合有多少,小于的组合有多少。
如果随着X的增大变量Y增大的值越多,降低的值越少,说明两个变量之间越正相关;如果随着X的增大变量Y增大的值越少,降低的值越多,说明两个变量之间越负相关;如果随着X的增大变量Y增大的值与降低的值的数量比较接近,说明两个变量之间相关性比较弱。
05
以上就是关于三种不同相关系数的一个简单介绍,平常大家应该对第一种皮尔逊相关系数了解比较多,但是严格意义上后两种要比第一种更加通用,而且适用场景更多一些,尤其是对异常值的影响。
当然了,我们在使用这些方法的过程中肯定是不需要去自己手动计算的,大家只需要明白其中的原理即可。这些相关性系数的求取在Python中都是有现成的函数供大家使用。df.corr()大家应该有人使用过,不知道你有没有看过这个函数里面的参数,这个函数里面有一个method参数,该参数有三个值可选:‘pearson’, spearman’,‘kendall’,分别对应我们上面的三种系数的求取。
本文就讲到这里,大家可以去使用起来啦。
以上是 【Python】统计科学之聊聊你知道和不知道的相关性系数 的全部内容, 来源链接: utcz.com/a/108964.html






得票时间