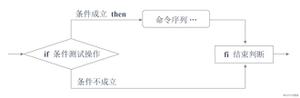
使用二分法（BisectionMethod）求平方根。

  • Z时代
  • 2024-01-10
  • 分类：综合

python

使用二分法（Bisection Method）求平方根。

def sqrtBI(x, epsilon):
    assert x>0, "X must be non-nagtive, not " + str(x)
    assert epsilon > 0, "epsilon must be postive, not " + str(epsilon)
    low = 0
    high = x
    guess = (low + high)/2.0
    counter = 1
    while (abs(guess ** 2 - x) > epsilon) and (counter <= 100):
        if guess ** 2 < x:
            low = guess
        else :
            high = guess
        guess = (low + high)/2.0
        counter += 1
    return guess

验证一下。

>>> sqrtBI(2,0.000001)

>>> 1.41421365738

上面的方法，如果 X<1 ，就会有问题。因为 X （X<1）的平方根不在 [0, x] 的范围内。例如，0.25，它的平方根——0.5 不在 [0, 0.25] 的区间内。

>>> sqrtBI(0.25,0.000001)

>>> 0.25

那如何求0.25的平方根呢？

只要略微改动上面的代码即可。注意6行和7行的代码。

def sqrtBI(x, epsilon):
    assert x>0, "X must be non-nagtive, not " + str(x)
    assert epsilon > 0, "epsilon must be postive, not " + str(epsilon)
    low = 0
    high = max(x, 1.0)
    ## high = x
    guess = (low + high)/2.0
    counter = 1
    while (abs(guess ** 2 - x) > epsilon) and (counter <= 100):
        if guess ** 2 < x:
            low = guess
        else :
            high = guess
        guess = (low + high)/2.0
        counter += 1
    return guess

验证一下：

>>> sqrtBI(0.25,0.000001)

>>> 0.5


以上是 使用二分法（BisectionMethod）求平方根。 的全部内容， 来源链接： utcz.com/z/523342.html

回到顶部