如何用高级数据结构,解决算法难题?

作者简介:苏勇,资深软件工程师。
本文选自:拉勾教育专栏《300分钟搞定数据结构与算法" title="数据结构与算法">数据结构与算法》
你好,我是苏勇,在今天的分享中,我将重点介绍一种高级的数据结构:优先队列。
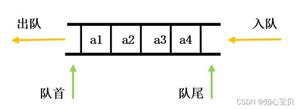
优先队列(Priority Queue)
和普通队列不同的是,优先队列最大的作用是能保证每次取出的元素都是队列中优先级别最高的,这个优先级别可以是自定义的,例如,数据的数值越大,优先级越高,或者是数据的数值越小,优先级越高,优先级别甚至可以通过各种复杂的计算得到。
优先队列最常用的场景是从一堆杂乱无章的数据当中按照一定的顺序(或者优先级)逐步地筛选出部分的乃至全部的数据。
例如,任意给定一个数组,要求找出前k大的数。试想一下,最直接的办法就是先对这个数组进行排序,然后依次输出前k大的数,这样的复杂度将会是O(nlogn),其中,n是数组的元素个数。
有没有更好的办法呢?如果我们借用优先队列,就能将复杂度优化成O(k + nlogk),当数据量很大(即n很大),而k相对较小的时候,显然,利用优先队列能有效地降低算法复杂度,其本质就在于,要找出前k大的数,我们并不需要对所有的数进行排序。现在问题来了,这个复杂度是如何计算出来的呢?要理解它,我们先来看看优先队列的实现方法。
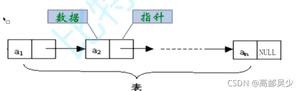
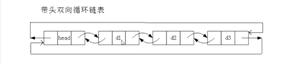
优先队列的本质是一个二叉堆结构,堆在英文里叫Binary Heap,它是利用一个数组结构来实现的完全二叉树。换句话说,优先队列的本质是一个数组,数组里的每个元素既有可能是其他元素的父节点,也有可能是其他元素的子节点,而且,每个父节点只能有两个子节点,这就很像一棵二叉树的结构了。
这里有三个重要的性质需要牢记:
- 数组里的第一个元素array[0]拥有最高的优先级别。
- 给定一个下标 i,那么对于元素 array[i] 而言:
它的父节点所对应的元素下标是 (i-1) / 2
它的左孩子所对应的元素下标是 2*i + 1
它的右孩子所对应的元素下标是 2*i + 2
- 数组里每个元素的优先级别都要高于它两个孩子的优先级别。
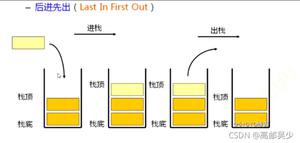
优先队列最基本的操作就是两个:
- 向上筛选(sift up / bubble up)
- 向下筛选(sift down / bubble down)
本文选自:拉勾教育专栏《300分钟搞定数据结构与算法》
什么是向上筛选呢?当有新的数据加入到优先队列中,新的数据首先被放置在二叉堆的底部,然后不断地对它进行向上筛选的操作,即如果发现它的优先级别比父节点的优先级别还要高,那么就和父节点的元素相互交换,再接着网上进行比较,直到无法再继续交换为止。由于二叉堆是一棵完全二叉树,并假设堆的大小为k,因此整个过程其实就是沿着树的高度网上爬,所以只需要O(logk)的时间。
3
/
5 9 3, 5, 9
3
/
5 9 3 ,5,9,2
/
2
3
/
2 9 3,2,9,5
/
5
2
/
3 9 2,3,9,5
/
5
如何进行向下筛选呢?当堆顶的元素被取出时,我们要更新堆顶的元素来作为下一次按照优先级顺序被取出的对象,我们所需要的是将堆底部的元素放置到堆顶,然后不断地对它执行向下筛选的操作,在这个过程中,该元素和它的两个孩子节点对比,看看哪个优先级最高,如果优先级最高的是其中一个孩子,就将该元素和那个孩子进行交换,然后反复进行下去,直到无法继续交换为止,整个过程就是沿着树的高度往下爬,所以时间复杂度也是O(logk)。
2
/
3 9 2,3,9,5
/
5
5
/
3 9 5,3,9
3
/
5 9 3,5,9
因此,无论是添加新的数据还是取出堆顶的元素,都需要O(logk)的时间。
另外一个最重要的时间复杂度是优先队列的初始化,这是分析运用优先队列性能时必不可少的,也是经常容易弄错的地方。
假设我们有n个数据,我们需要创建一个大小为n的堆,乍一看,每当把一个数据加入到堆里,我们都要对其执行向上筛选的操作,这样以来就是O(nlogn)。但是,在创建这个堆的过程中,二叉树的大小是从1逐渐增长到n的,所以整个算法的复杂度是:
本文选自:拉勾教育专栏《300分钟搞定数据结构与算法》
经过进一步的推导,最终的结果是O(n)。算法面试中是不要求推导的,你只需要记住,初始化一个大小为n的堆,所需要的时间是O(n)即可。
注:
向上筛选,用这个静态图
3
/
5 9
/
2
例题分析
LeetCode 第347题. Top K Frequent Words 从一系列单词中找出使用频率最高的前K个单词
这道题的输入是一个字符串数组,数组里的元素可能会重复一次甚至多次,要求按顺序输出前K个出现次数最多的字符串。
当我们拿到这个题目的时候,看到”前K个“这样的字眼就应该很自然地联想到运用优先队列。
那么优先级别怎么计算呢?让我们来分析一下,优先级别可以由字符串出现的次数来决定,出现的次数越多,优先级别越高,反之越低。
统计词频的最佳数据结构就是哈希表(Hash Map),利用一个哈希表,我们就能快速的知道每个单词出现的次数。
然后将单词和其出现的次数作为一个新的对象来构建一个优先队列,那么这个问题就很轻而易举地解决了。
可以看到,解这类求前K个的题目,关键是看如何定义优先级以及优先队列中元素的数据结构。这道题可以说是利用优先对列处理问题的典型,建议好好看看。
Desk (3)
/
car(2) book(1)
通过这节课的学习,我们详细了解到高级的数据结构:优先队列。本次分享就讲到这里,下节课我们将学习面试中常用的算法,好,我们下次再见!
查看后续内容:拉勾教育专栏《300分钟搞定数据结构与算法》
版权声明:本文版权归属拉勾教育及该专栏作者,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他方式复制发布/发表,违者必究。
以上是 如何用高级数据结构,解决算法难题? 的全部内容, 来源链接: utcz.com/z/515452.html