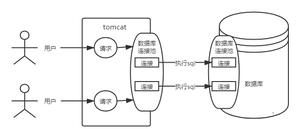
leecode4有序数组的中位数，并且要求算法的时间复杂度为O(log(m+n))

Z时代
2024-01-10
分类：综合

//给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。 
//
// 请你找出这两个有序数组的中位数，并且要求时间复杂度" title="算法的时间复杂度">算法的时间复杂度为 O(log(m + n))。 
//
// 你可以假设 nums1 和 nums2 不会同时为空。 
//
// 示例 1: 
//
// nums1 = [1, 3]
//nums2 = [2]
//
//则中位数是 2.0
// 
//
// 示例 2: 
//
// nums1 = [1, 2]
//nums2 = [3, 4]
//
//则中位数是 (2 + 3)/2 = 2.5
// 
// Related Topics 数组 二分查找 分治算法
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int sum=nums1.length+nums2.length;
        int nums3[]=new int[sum];
        int i=0,j=0,temp=0;
        double res;
        while(temp<=sum/2)//将一半的数组排序即可
        {
            if(i<nums1.length&&j<nums2.length)//防止数组溢出
            {
                if(nums1[i]<nums2[j])
                {
                    nums3[temp++]=nums1[i++];
                }
                else
                {
                    nums3[temp++]=nums2[j++];
                }
            }
            else if(i>=nums1.length)//其中一个数组到末尾了
            {
                nums3[temp++]=nums2[j++];
            }
            else
            {
                nums3[temp++]=nums1[i++];
            }
        }
        if(sum%2==0)//偶数位个
        {
            res=((double)(nums3[sum/2]+nums3[sum/2-1]))/2; //需要强转一下类型
        }
        else
        {
            res=nums3[sum/2];//奇数位个
            System.out.println("res2"+res);
        }
        return res;
    }
}
//leetcode submit region end(Prohibit modification and deletion)