dijkstra算法解决单源最短路问题

简介
最近这段时间刚好做了最短路问题的算法报告,因此对dijkstra算法" title="dijkstra算法">dijkstra算法也有了更深的理解,下面和大家分享一下我的学习过程。
前言
呃呃呃,听起来也没那么难,其实,真的没那么难,只要弄清楚思路就很容易了。下面正经的跟大家说下解决问题的过程。
实现过程
我们先用一个d[i]数组表示起点到点i的直接距离,然后从d[i]数组中找最小的值所对应的点,然后看点与点i之间相连的点j,
然后比较d[j]和d[i]+w[i][j](w[i][j]表示的是点i到点j之间的距离)之间的大小,然后把d[j]和d[i]+w[i][j之间较小的一个赋值给
d[j],即d[j]=min(d[j],d[i]+w[i][j])。并把点i标记已访问。
然后我们不断的进行上面的操作,直到把所有的点全部访问完毕。
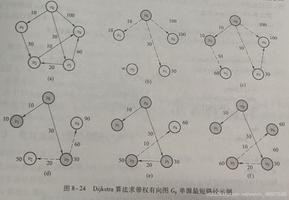
下面是操作过程的流程图
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
解决问题
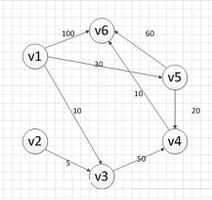
题目大概意思:“比如说,在一张无向图中,给了结点数和边的数目让你求出起点到其他各点的最短距离。”
输入数据为:
下面是具体实现的代码:
/*dijkstra算法*/#include
<iostream>constlonglong maxint = 100000000000;
usingnamespace std;
constint maxn = 10010;
int n, m;
int a, b, v, w[maxn][maxn];
int dis[maxn]; //记录起点到别的结点之间的距离
bool s[maxn]; //标记这个点是否在图中
//v0=1;
void dijkstra(int v0) {
dis[0] = 0;
dis[v0] = 0;
s[v0] = true;
for (int i = 1; i <= n; ++i) { //将每个点到起点的距离更新一下
dis[i] = w[v0][i];
s[i] = false;
}
while (1) {
int min = maxint;
int u = -1; //标志变量
for (int j = 1; j <= n; ++j) {
if ((!s[j]) && dis[j] < min) { //找出不在图里面且权值最小的点
u = j; //将这个点记录下来
min = dis[j];
}
}
if (u == -1) break;
s[u] = true; //将这个点放入图中
for (int j = 1; j <= n; ++j) {
if ((!s[j]) && dis[u] + w[u][j] < dis[j]) {
dis[j] = dis[u] + w[u][j]; //松弛操作 更新起点到这个点的距离
}
}
}
}
int main() {
cout << "请输入结点数目和点数: ";
while (cin >> n >> m && n&&m) { //输入点的数目和边的数目
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
w[i][j] = maxint; //先将每条边的距离弄成很大,后面如果两条边的权值不等于这个很大的数,则说明两个数之间有边
}
}
cout << "请输入两点之间的距离" << endl;
for (int i = 0; i < m; ++i) {
cin >> a >> b >> v;
w[a][b] = v; //因为无向图
w[b][a] = v; //所以两个都赋值
}
dijkstra(1);
for (int i = 2; i <= n; ++i) {
if(w[1][i]!=maxint)
cout << "起点1到点" << i << "的最短距离是" << dis[i] << endl;
else cout << "起点1到点" << i << "没有路径"<< endl;
}
// cout << dis[n] << endl;
}
}
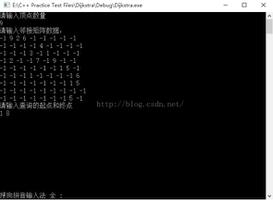
程序运行的结果就是这样的。。。。。。。
好了,到此为止,朴素版本的dijkstra算法就讲完了,感觉好low啊【嘤嘤嘤】
那个那个,估计下一篇博客会把堆优化版本的dijkstra算法更新一下,然后,,,下一次更新不知道是啥时候了,哈哈!
以上是 dijkstra算法解决单源最短路问题 的全部内容, 来源链接: utcz.com/z/509894.html