红黑树详解

1.为什么需要红黑树?
对于二叉搜索树,如果插入的数据是随机的,那么它就是接近平衡的二叉树,平衡的二叉树,它的操作效率(查询,插入,删除)效率较高,时间复杂度是O(logN)。但是可能会出现一种极端的情况,那就是插入的数据是有序的(递增或者递减),那么所有的节点都会在根节点的右侧或左侧,此时,二叉搜索树就变为了一个链表,它的操作效率就降低了,时间复杂度为O(N),所以可以认为二叉搜索树的时间复杂度介于O(logN)和O(N)之间,视情况而定。那么为了应对这种极端情况,红黑树就出现了,它是具备了某些特性的二叉搜索树,能解决非平衡树问题,红黑树是一种接近平衡的二叉树。
2.红黑树的特性有哪些?
首先,红黑树是一个二叉搜索树,它同时满足以下特性:
(1) 每个节点要么是黑色,要么是红色
(2) 根节点是黑色
(3) 如果节点是红色的,那么它的子节点必须是黑色的(反之,不一定需要成立)
(4) 从根节点到叶节点或空子节点的每条路径,都包含相同数目的黑色节
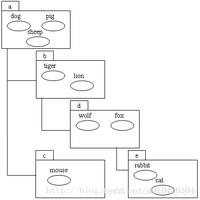
通过看图来理解以上四个特性
3.红黑树的效率
红黑树的查找,插入和删除操作,时间复杂度都是O(logN)。查找操作时,它和普通的相对平衡的二叉搜索树的效率相同,都是通过相同的方式来查找的,没有用到红黑树特有的特性。但,如果插入的时候是有序数据,那么红黑树的查询效率就比二叉搜索树要高了,因为此时二叉搜索树不是平衡树,它的时间复杂度O(N)。插入和删除操作时,由于红黑树的每次操作平均要旋转一次和变换颜色,所以它比普通的二叉搜索树效率要低一点,不过时间复杂度仍然是O(logN)。总之,红黑树的优点就是对有序数据的查询操作不会慢到O(logN)的时间复杂度。
4.对旋转的理解
在红黑树中,插入或者删除数据时,为了保持红黑树的那五个特性,需要进行旋转和变换颜色的操作。旋转必须要一次性做两件事情:
* 使一些节点上升,一些节点下降,帮助树平衡
* 保证不破坏二叉搜索树的特征
旋转分为左旋转和右旋转,那么我们就看下左旋转和右旋转是怎么回事。
4.1 左旋转
此处,以50为支点进行逆时针旋转,然后75成为了顶点,50成为了75的左子节点,65成为了50的右子节点,这个操作就是左旋转。
4.2 右旋转
此处,以75为支点顺时针旋转,然后50成为了顶点,75成为了50的右子节点,65成为了75的左子节点,这就是右旋转操作。
5.插入操作
在介绍插入操作前,先约定一下各个节点的名称。看图:
在红黑树中,插入一个节点,都执行了哪些操作呢?
首先,查找要插入节点的位置,然后给予颜色(红色或者黑色),但是为了保证红黑树的特性,需要进行旋转或者更改颜色,需要注意的是,在旋转前和旋转后,红黑树一直都是一个二叉搜索树,二叉搜索树的特征从未改变过。
这里,对于新插入的节点,我们给予的颜色是红色,是因为为了和红黑树的第(4)条特性不冲突: 从根节点到叶节点或空子节点的每条路径,都包含相同数目的黑色节点。这样就少了很多操作。然后看其它几个特性
* 对于(1)特性:每个节点要么是黑色,要么是红色,不冲突。
* 对于(2)特性:根节点是黑色,如果插入的节点不是根节点,也不冲突。如果是根节点,那么直接给予颜色黑色
那么,唯一需要满足的特性就是(3):如果节点是红色的,那么它的子节点必须是黑色的。这里,当我们给予新插入的节点颜色是红色时,需要根据父节点的不同情况做不同的处理,以满足这个特性。有以下几种情况:
根据代码来理解这几种情况:
/* 红黑树修正程序 */void insert_repair_tree(struct node* n) {
//情况一:节点N的父节点为null,说明该节点是根节点
if (parent(n) == NULL) {
insert_case1(n);
} elseif (parent(n)->color == BLACK) {
//情况二:父节点是黑色
insert_case2(n);
} elseif (uncle(n)->color == RED) {
//情况三: 父节点和叔叔节点都是红色
insert_case3(n);
} else {
//情况四:父节点是红色,叔叔节点是黑色
insert_case4(n);
}
}
5.1:如果新插入节点是根节点,那么给予该节点颜色是黑色
看代码:
/* 情况一:插入的节点是根节点 */void insert_case1(struct node* n)
{
if (parent(n) == NULL)
n->color = BLACK;
}
5.2:如果新插入节点的父节点是黑色,那么给予该节点是红色不会对该红黑树有任何影响,所以不做任何处理。
看代码:
/* 情况二:父节点是黑色 */void insert_case2(struct node* n)
{
return; /* Do nothing since tree is still valid */
}
5.3:如果新插入节点的父节点是红色,同时叔叔节点也是红色
需要将父亲节点和叔叔节点重新绘制为黑色,祖父节点绘制为红色。但是,如果此处祖父节点为根节点,那么需要调用红黑树修正程序,将祖父节点绘制为黑色。
看代码:发现看代码比看图要更容易理解,并且逻辑也更严谨,对于父亲节点和叔叔节点都是红色时,发现其他文章都没有考虑祖父节点为根节点的情况,这里图就省了。
/* 情况三:父节点和叔叔节点都是红色 */void insert_case3(struct node* n)
{
parent(n)->color = BLACK;
uncle(n)->color = BLACK;
grandparent(n)->color = RED;
//调用红黑树修正程序
insert_repair_tree(grandparent(n));
}
5.4:如果新插入节点的父节点是红色,同时叔叔节点是黑色
看代码:
/* 情况四:第一步 */void insert_case4(struct node* n)
{
struct node* p = parent(n);
struct node* g = grandparent(n);
if (n == g->left->right) {
/* 如果父节点是祖父节点的左子节点,新插入节点是父节点的右子节点,那么以父节点为支点左旋 */
rotate_left(p);
n = n->left;
} elseif (n == g->right->left) {
/* 如果父节点是祖父节点的右子节点,新插入节点是父节点的左子节点,那么以父节点为支点右旋 */
rotate_right(p);
n = n->right;
}
insert_case4step2(n);
}
/* 情况四:第二步 */
/* 在第二步时:当前节点n肯定处于 祖父节点左子节点的左侧,或者祖父节点右子节点的右侧 */void insert_case4step2(struct node* n)
{
struct node* p = parent(n);
struct node* g = grandparent(n);
if (n == p->left)
/* 以祖父节点为支点进行右旋 */
rotate_right(g);
else
rotate_left(g);
p->color = BLACK;
g->color = RED;
}
在满足父节点是红色,叔叔节点是黑色的条件下,我们可以分以下几种情况:
情况(a):父节点p是祖父节点g的左子节点,新插入节点n是父节点p的右子节点
处理:以父节点为支点左旋,然后以祖父节点为支点进行右旋,最后给父节点(第一次旋转后的父节点)绘制为黑色,给祖父节(第一次旋转后的祖父节点)点绘制为红色
看图:
情况(b):父节点p是祖父节点g的右子节点,新插入节点n是父节点p的左子节点
处理:以父节点为支点进行右旋,然后以祖父为支点进行左旋,最后给父节点(第一次旋转后的父节点)绘制为黑色,给祖父节(第一次旋转后的祖父节点)点绘制为红色
看图:
情况(c):父节点p是祖父节点g的左子节点,新插入节点n是父节点p的左子节点
处理:以祖父节点为支点进行右旋,最后给父节点绘制为黑色,给祖父节点绘制为红色,也就是直接调用第二步的方法 insert_case4step2
情况(d):父节点p是祖父节点g的右子节点,新插入节点n是父节点p的右子节点
处理:以祖父为支点进行左旋,最后给父节点绘制为黑色,给祖父节点绘制为红色,也就是直接调用第二步的方法 insert_case4step2
6 删除操作
对于删除操作,处理的逻辑是:根据二叉搜索树的特点找到被删除的节点,将其删除掉,然后再通过改变颜色和旋转操作保持其红黑树的特性。此处我们统一规定被删除节点是D,真正被删除节点为RD,真正被删除节点的兄弟节点是B,真正被删除节点的父节点是P,B的两个子节点是BL和BR。删除操作有三种情况:
6.1 被删除节点为叶子节点,分为两种情况:
情况(a):该叶子节点是红色
处理:直接删除
情况(b):该叶子节点是黑色,
处理:删除节点,然后旋转和变换颜色。
6.2 被删除节点只有一个子节点,那么使被删除节点的父节点指向被删除节点的子节点,然后通过改变节点颜色和旋转来保持红黑树特性
6.3 被删除节点D有两个子节点,那么可以将被删除节点D的后继节点(D的右子树中的最小元素RD)的值赋值给被删除节点D,但是被删除节点D的颜色不做改变,此时删除操作就转化为了删除后继节点RD的情况了。那么删除RD的情况又分为五种:
情况(a): RD节点是红色的
处理:如果RD节点是红色的,那么它的父节点和右子节点应该是黑色的,当删除RD节点时,直接把RD节点的父节点指向RD节点的右子节点即可。
下面四种情况RD节点都是黑色的
情况(b):RD的兄弟节点B为红色
处理:如果B节点为红色,那么P节点和B的两个子节点都是黑色。交换B节点和P节点的颜色,然后以P节点为支点进行左旋转。这样处理后,就将情况(b)转为(c),(d),(e)中的一种。
看图:
情况(c):
后续更新。。。
参考资料:
模拟红黑树:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
维基百科红黑树:https://en.wikipedia.org/wiki/Red%E2%80%93black_tree#Insertion
以上是 红黑树详解 的全部内容, 来源链接: utcz.com/z/509314.html