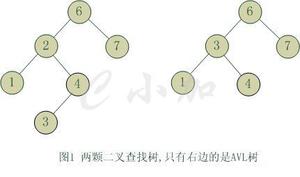
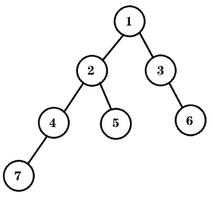
二叉树链表C++实现

结点的构造
源代码:https://github.com/cjy513203427/C_Program_Base/tree/master/57.%E4%BA%8C%E5%8F%89%E6%A0%91%E9%93%BE%E8%A1%A8%E5%AE%9E%E7%8E%B0
#pragma once#ifndef NODE_H
#define NODE_Hclass Node
{
public:
Node();
Node *SearchNode(int nodeIndex);
void DeleteNode();
void PreorderTraversal();
void InorderTraversal();
void PostorderTraversal();
int index;
int data;
Node *pLChild;
Node *pRChild;
Node *pParent;
};
#endif// !NODE_H
需要实现的方法
#pragma once#ifndef TREE_H
#define TREE_H#include
"Node.h"class Tree
{
public:
Tree();//创建树
~Tree();//销毁树
Node *SearchNode(int nodeIndex);//搜索结点
bool AddNode(int nodeIndex, int direction, Node* pNode);//添加结点
bool DeleteNode(int nodeIndex, Node* pNode);//删除结点
void PreorderTraversal();//前序遍历
void InorderTraversal();//中序遍历
void PostorderTraversal();//后序遍历
private:
Node * m_pRoot;
};
#endif// ! TREE_H
创建树
申请一段内存
Tree::Tree(){
m_pRoot
= new Node();};
创建结点
Node::Node(){
index
= 0; data
= 0; pLChild
= NULL; pRChild
= NULL; pParent
= NULL;}
销毁树
调用Node的DeleteNode方法
Tree::~Tree(){
m_pRoot->DeleteNode();
}
如果当前Node对象(this)的pLChild不为空,递归调用DeleteNode方法,this->pLChild变成了新的this,直到delete this销毁掉
如果当前Node对象(this)的pRChild不为空,递归调用DeleteNode方法,this->pRChild变成了新的this,直到delete this销毁掉
如果当前Node对象(this)的pParent不为空,如果父节点的左子节点等于当前Node对象,将当前结点置空
如果当前Node对象(this)的pParent不为空,如果父节点的右子节点等于当前Node对象,将当前结点置空
思路:指定索引向下搜索从最底层子节点开始删除,再往上回到指定索引并删除,删除的顺序是后序
void Node::DeleteNode(){
if (this->pLChild != NULL) {
this->pLChild->DeleteNode(); }
if (this->pRChild != NULL) {
this->pRChild->DeleteNode(); }
if (this->pParent != NULL) {
if (this->pParent->pLChild == this) {
this->pParent->pLChild = NULL; }
if (this->pParent->pRChild == this) {
this->pParent->pRChild = NULL; }
}
deletethis;}
搜索结点
传入索引,调用Node的SearchNode方法
Node *Tree::SearchNode(int nodeIndex){
return m_pRoot->SearchNode(nodeIndex);}
Node的SearchNode()
如果索引和传入索引相等,返回当前Node对象
当this对象的左子节点不为空,当左子节点索引等于传入索引,返回当前对象的子节点
否则继续对当前对象的左子节点搜索,搜索结果赋值给temp,当temp不为空,返回temp
对右子节点的逻辑同上
否则返回为空
思路:从上向下搜索,顺序为前序
Node *Node::SearchNode(int nodeIndex){
if (this->index == nodeIndex) {
returnthis; }
Node
*temp = NULL;if (this->pLChild != NULL) {
if (this->pLChild->index == nodeIndex) {
returnthis->pLChild; }
else {
temp
= this->pLChild->SearchNode(nodeIndex);if (temp != NULL) {
return temp; }
}
}
if (this->pRChild != NULL) {
if (this->pRChild->index == nodeIndex) {
returnthis->pRChild; }
else {
temp
= this->pRChild->SearchNode(nodeIndex);if (temp != NULL) {
return temp; }
}
}
return NULL;}
添加结点
传入索引,direction=0添加左子节点,direction=1添加右子节点,传入pNode参数
先搜索结点并保存在temp中,temp为空返回错误
申请内存给node,为空返回错误
将pNode的index和data分别赋值给node的index和data
node的pParent指针指向temp,temp为指定索引的父节点
direction=0,将temp的pLChild指针指向node
direction=1,将temp的pRChild指针指向node
bool Tree::AddNode(int nodeIndex, int direction, Node* pNode){
Node
*temp = SearchNode(nodeIndex);if (temp == NULL) {
returnfalse; }
Node
*node = new Node();if (node == NULL) {
returnfalse; }
node
->index = pNode->index; node
->data = pNode->data; node
->pParent = temp;if (direction == 0) {
temp
->pLChild = node; }
if (direction == 1) {
temp
->pRChild = node; }
returntrue;}
删除结点
传入nodeIndex,pNode参数
搜索结点保存在temp
temp为空,返回错误
pNode不为空,将的temp的data赋值给pNode的data,做返回值使用
调用Node的DeleteNode方法,参见销毁树
bool Tree::DeleteNode(int nodeIndex, Node* pNode){
Node
*temp = SearchNode(nodeIndex);if (temp == NULL) {
returnfalse; }
if (pNode != NULL) {
pNode
->data = temp->data; }
temp
->DeleteNode();returntrue;}
前序遍历
调用了Node的PreorderTraversal()
void Tree::PreorderTraversal(){
m_pRoot
->PreorderTraversal();}
Node的PreorderTraversal()
先输出根节点
左子结点不为空递归,输入当前结点
右子节点不为空递归,输入当前结点
递归的算法最好对着源码打断点,就能看懂了
void Node::PreorderTraversal(){
cout
<< this->index<<""<<this->data << endl;if (this->pLChild != NULL) {
this->pLChild->PreorderTraversal(); }
if (this->pRChild != NULL) {
this->pRChild->PreorderTraversal(); }
}
中序遍历和后序遍历
中序遍历:左根右
后序遍历:左右根
void Tree::InorderTraversal(){
m_pRoot
->InorderTraversal();}
void Tree::PostorderTraversal(){
m_pRoot
->PostorderTraversal();}
逻辑与前序遍历代码相似
this->index和this->data就是根节点的内容
左右结点进行递归
void Node::InorderTraversal(){
if (this->pLChild != NULL) {
this->pLChild->InorderTraversal(); }
cout
<< this->index << "" << this->data << endl;if (this->pRChild != NULL) {
this->pRChild->InorderTraversal(); }
}
void Node::PostorderTraversal(){
if (this->pLChild != NULL) {
this->pLChild->PostorderTraversal(); }
if (this->pRChild != NULL) {
this->pRChild->PostorderTraversal(); }
cout
<< this->index << "" << this->data << endl;}
补充
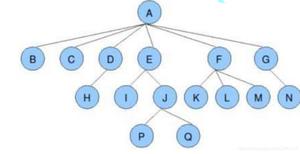
根据前序和中序推断出二叉的结构
前序遍历为ABDEGCFH
后序遍历为DBGEACHF
以上是 二叉树链表C++实现 的全部内容, 来源链接: utcz.com/z/508951.html