二叉树的前序、中序、后序遍历,通过递归和非递归的方式实现【Java】

概述
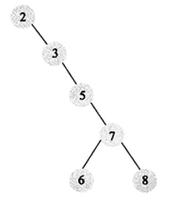
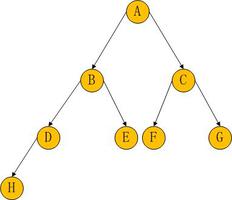
二叉树的遍历" title="二叉树的遍历">二叉树的遍历,一个老生常谈的问题,大学的时候就天天学习,但是那时候大多是了解每中遍历的方式,但是并没有用代码实现,工作之后,使用代码实现一下。
三种遍历方式的区别
具体的介绍我这里就不说了,只总结性的说一下,所谓的前序,中序,后序,的前中后,其实就是根节点被访问的前中后,前序遍历就是根节点在最开始,中序遍历就是根节点在中间,后序遍历就是根节点在最后,当然这个根节点并不一定是二叉树的唯一根节点,而是每个节点只要有子节点,那这个节点其实都可以看作子节点的根节点。
下面就上代码
通过java自己实现二叉树
先定义节点
1 package com.example.demo.tree;2
3 /**
4 * @author steve
5 * @date 2020/4/18 3:16 下午
6 */
7 public class Node<E> {
8 public Node<E> left;
9 public Node<E> right;
10 public Node<E> parent;
11 public E element;
12 public Node(E element){
13 this.element = element;
14 }
15 }
View Code
定义二叉树
1 package com.example.demo.tree;2
3 import com.sun.scenario.effect.impl.sw.sse.SSEBlend_SRC_OUTPeer;
4 import org.omg.PortableInterceptor.INACTIVE;
5
6 import java.util.Comparator;
7
8 /**
9 * @author steve
10 * @date 2020/4/16 10:03 上午
11 */
12 public class BinaryTree<E> {
13
14 private int size;
15 public Node<E> root;
16 private Comparator<E> comparator;
17
18 public BinaryTree(Comparator<E> comparator){
19 this.comparator = comparator;
20 }
21
22 public BinaryTree(){
23 this(null);
24 }
25
26 public void add(E element){
27 if (root == null){
28 Node node = new Node(element);
29 root = node;
30 }else {
31 Node<E> parent = root;
32 Node<E> node = root;
33 int com = 0;
34 while (node != null){
35 parent = node;
36 if (comparator == null){
37 com = ((Comparable)node.element).compareTo(element);
38 }else {
39 System.out.println("-------------");
40 com = comparator.compare(node.element,element);
41 }
42 if (com > 0){
43 node = node.left;
44 }else if (com < 0){
45 node = node.right;
46 }else {
47 node.element = element;
48 return;
49 }
50 }
51 Node<E> newNode = new Node(element);
52 if (com > 0){
53 parent.left = newNode;
54 newNode.parent = parent.left;
55 }else{
56 parent.right = newNode;
57 newNode.parent = parent.right;
58 }
59 }
60 size ++;
61 }
62 public boolean isEmpty(){
63 return size == 0;
64 }
65 public int size(){
66 return size;
67 }
68
69 public String toString() {
70 String d = root == null ? null : root.element + "";
71 if (root == null){
72 return "root:"+d;
73 }else {
74 String b = root.left == null ? null : root.left.element + "";
75 String c = root.right == null ? null : root.right.element + "";
76 return "root:"+d + ", left:" + b + ", right:"+ c;
77 }
78
79 }
80
81
82 public static void main(String[] args) {
83 //这种方式就是匿名内部类,通过给一个类传一个接口作为参数,然后这个通过一个匿名内部类是实现这个接口来传入实现。
84 BinaryTree<Integer> binaryTree = new BinaryTree<>(new Comparator<Integer>() {
85 @Override
86 public int compare(Integer o1, Integer o2) {
87 return o1 - o2;
88 }
89 });
90
91 BinaryTree<Integer> binaryTree1 = new BinaryTree<>();
92 binaryTree1.add(1);
93 binaryTree1.add(2);
94 binaryTree1.add(0);
95 System.out.println(binaryTree1.size());
96 System.out.println(binaryTree.toString());
97 }
98 }
View Code
遍历二叉树
1 package com.example.demo.tree;2
3 import sun.tools.native2ascii.resources.MsgNative2ascii;
4
5 import java.util.*;
6
7 /**
8 * @author steve
9 * @date 2020/4/18 2:58 下午
10 * 遍历二叉树,分别使用递归和迭代进行前序中序后序遍历一颗二叉树
11 */
12 public class TraversBinaryTree {
13
14 /**
15 * 前序遍历
16 * 从根节点开始,先遍历左子树,后遍历右子树
17 */
18 public static void preOrderTraveral(Node<Integer> node){
19 if (node == null) return;
20 System.out.println(node.element);
21 preOrderTraveral(node.left);
22 preOrderTraveral(node.right);
23 }
24
25 /**
26 * 前序遍历,不使用递归实现
27 * 解释:前序遍历是最简单的,因为这个是从头开始的,不用像中序遍历和后序遍历一样,都是从最低级的左孩子开始,所以这个,只需要一直入栈右孩子,
28 * 左孩子,就可以了,其实这个过程一遍下来之后,所有的左孩子都出栈了,剩下的就是右孩子,那再慢慢出栈就可以了。
29 * @param node
30 */
31 public static void preOrderTraveralUseStack(Node<Integer> node){
32 Stack<Node<Integer>> stack = new Stack<>();
33 stack.push(node);
34 while (!stack.isEmpty()){
35 Node<Integer> node1 = stack.pop();
36 System.out.println(node1.element);
37 if (node1.right != null){
38 stack.push(node1.right);
39 }
40 if (node1.left != null){
41 stack.push(node1.left);
42 }
43 }
44 }
45
46 /**
47 * 中序遍历二叉树
48 * 根节点在中间,从最左边的节点开始,先左后中,后右,遍历
49 */
50 public static void inOrderTraveral(Node<Integer> node){
51 if (node == null) return;
52 inOrderTraveral(node.left);
53 System.out.println(node.element);
54 inOrderTraveral(node.right);
55
56 }
57
58 /**
59 * 中序遍历,不使用递归实现
60 * 解释:这个其实比后序遍历简单,因为,这个先压入中,之后压入左,在出栈的时候,可以直接按照这个顺序反着出栈,然后在这个过程中
61 * 只需要判断有没有右孩子,而不用担心右孩子重复入栈的问题,但是后序遍历就需要考虑这个问题
62 * @param node
63 */
64 public static void inOrderTraveralUseStack(Node<Integer> node){
65 if (node == null) return;
66 Stack<Node<Integer>> stack = new Stack<>();
67 stack.push(node);
68 while (!stack.isEmpty()){
69 if (node != null && node.left != null){
70 stack.push(node.left);
71 node = node.left;
72 }else {
73 //已经弹出来的节点,其左孩子不能再入栈
74 node = stack.pop();
75 System.out.println(node.element);
76 if (node.right != null){
77 stack.push(node.right);
78 node = node.right;
79 }else {
80 node = null;
81 }
82 }
83 }
84
85 }
86
87 /**
88 * 后序遍历
89 * 根节点最后遍历,先左后右,之后中间的
90 */
91 public static void postOrderTraveral(Node<Integer> node){
92 if (node == null) return;;
93
94 postOrderTraveral(node.left);
95 postOrderTraveral(node.right);
96 System.out.println(node.element);
97 }
98
99 /**
100 * 后序遍历,不使用递归,使用栈的方式实现
101 * 1.先把左孩子压入栈,如果没有左孩子了,弹出左孩子
102 * 2.然后把右孩子压入栈,如果没有了,就弹出
103 * 注意:
104 * 1.这里要注意两个点,第一个点就是如果一个节点的左孩子和右孩子都已经判断完了,那么就把这个节点置为null
105 * 2.如果一个节点的右孩子已经处理过了,就不要重复入栈
106 * 总结:
107 * 1.不能重复入栈,无论是左孩子还是右孩子
108 * @param node
109 */
110 public static void postOrderTraveralUseStack(Node<Integer> node){
111 if (node == null) return;
112 Stack<Node<Integer>> stack = new Stack<>();
113 stack.add(node);
114 Node<Integer> node2 = null;
115 while (!stack.isEmpty()){
116 if (node != null && node.left != null){
117 stack.push(node.left);
118 node = node.left;
119 }else {
120 node = stack.peek();
121 if (node.right != null && node.right != node2){
122 stack.push(node.right);
123 //这里为了防止右孩子重复入栈
124 node2 = node.right;
125 node = node.right;
126 }else {
127 stack.pop();
128 System.out.println(node.element);
129 //这里为了防止右孩子重复入栈
130 node2 = node;
131 //这里为了防止左孩子重复入栈
132 node = null;
133 }
134 }
135 }
136 }
137
138 /**
139 * 层序遍历二叉树
140 * 使用队列实现,而不是栈
141 */
142 public static void levelOrderTraveral(Node<Integer> node){
143 Queue<Node<Integer>> queue = new LinkedList<>();
144 queue.add(node);
145 while(!queue.isEmpty()){
146 Node<Integer> node1 = queue.peek();
147 queue.poll();
148 System.out.println(node1.element);
149 if (node1.left != null){
150 queue.add(node1.left);
151 }
152 if (node1.right != null){
153 queue.add(node1.right);
154 }
155 }
156 }
157
158 public static void main(String[] args) {
159 BinaryTree<Integer> binaryTree = new BinaryTree<>();
160 binaryTree.add(7);
161 binaryTree.add(4);
162 binaryTree.add(10);
163 binaryTree.add(9);
164 binaryTree.add(11);
165 binaryTree.add(5);
166 binaryTree.add(3);
167 System.out.println("------------preorder traveral use recursion---------");
168 TraversBinaryTree.preOrderTraveral(binaryTree.root);
169 System.out.println("------------preorder traveral use stack");
170 TraversBinaryTree.preOrderTraveralUseStack(binaryTree.root);
171 System.out.println("-------------inorder traveral use recursion-------------------");
172 TraversBinaryTree.inOrderTraveral(binaryTree.root);
173 System.out.println("-------------inorder traveral use stack----------------");
174 TraversBinaryTree.inOrderTraveralUseStack(binaryTree.root);
175 System.out.println("--------------postorder traveral use recursion------------------");
176 TraversBinaryTree.postOrderTraveral(binaryTree.root);
177 System.out.println("--------------postorder traveral use stack-----------");
178 TraversBinaryTree.postOrderTraveralUseStack(binaryTree.root);
179 System.out.println("--------------------------------");
180 TraversBinaryTree.levelOrderTraveral(binaryTree.root);
181 }
182
183 }
View Code
总结
不知道是年龄大了,还是智商本身太低,通过非递归的方式实现二叉树的遍历,想了好久都没有思路,只有前序遍历是自己独立实现的,后面的中序和后序都是参考网上的代码,不过也许这个也是一个熟能生巧的事。
以上是 二叉树的前序、中序、后序遍历,通过递归和非递归的方式实现【Java】 的全部内容, 来源链接: utcz.com/z/394532.html