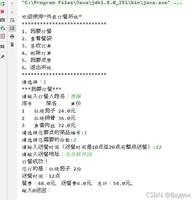
二叉树的java实现

import java.util.Arrays;import java.util.Stack;
// 链式存储的二叉树
public class BSTree {
private TreeNode root = null;
public TreeNode getRoot() {
return root;
}
public BSTree(TreeNode root) {
this.root = root;
}
public boolean isEmpty() {
return root == null;
}
// 树的高度
public int height() {
return TreeNode.height(root);
}
// 节点个数
public int size() {
return TreeNode.size(root);
}
// 返回树中某节点的父节点
public TreeNode parent(TreeNode element) {
return (root == null || root == element) ? null : TreeNode.getParent(root, element);
}
// 定义树的节点
private static class TreeNode {
private int data;
private TreeNode leftChild = null;
private TreeNode rightChild = null;
public TreeNode(int data) {
this.data = data;
this.leftChild = null;
this.rightChild = null;
}
public static TreeNode getParent(TreeNode subTree, TreeNode element) {
if (subTree == null)
return null;
if (subTree.leftChild == element || subTree.rightChild == element)
return subTree;
TreeNode p = null;
// 递归左右子树
if ((p = getParent(subTree.leftChild, element)) != null)
return p;
else
return getParent(subTree.rightChild, element);
}
public static TreeNode getLeftChildNode(TreeNode element) {
return (element != null) ? element.leftChild : null;
}
public static TreeNode getRightChildNode(TreeNode element) {
return (element != null) ? element.rightChild : null;
}
public static int height(TreeNode subTree) {
if (subTree == null)
return 0;// 递归结束:空树高度为0
else {
int i = height(subTree.leftChild);
int j = height(subTree.rightChild);
return (i < j) ? (j + 1) : (i + 1);
}
}
public static int size(TreeNode subTree) {
if (subTree == null) {
return 0;
} else {
return 1 + size(subTree.leftChild) + size(subTree.rightChild);
}
}
// 在释放某个结点前, 该结点的左右子树应该已经释放, 所以应该采用后续遍历
public static void destroySubTree(TreeNode subTree) {
// 删除根为subTree的子树
if (subTree != null) {
destroySubTree(subTree.leftChild);
destroySubTree(subTree.rightChild);
// 删除根结点
subTree = null;
}
}
public static void visted(TreeNode subTree) {
System.out.println("data: " + subTree.data);
}
// 前序遍历
public static void preOrder(TreeNode subTree) {
if (subTree != null) {
visted(subTree);
preOrder(subTree.leftChild);
preOrder(subTree.rightChild);
}
}
// 中序遍历
public static void inOrder(TreeNode subTree) {
if (subTree != null) {
inOrder(subTree.leftChild);
visted(subTree);
inOrder(subTree.rightChild);
}
}
// 后续遍历
public static void postOrder(TreeNode subTree) {
if (subTree != null) {
postOrder(subTree.leftChild);
postOrder(subTree.rightChild);
visted(subTree);
}
}
// 前序遍历的非递归实现
public static void nonRecPreOrder(TreeNode subTree) {
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode node = subTree;
while (node != null || stack.size() > 0) {
if (node != null) {
visted(node);
stack.push(node);
node = node.leftChild;
} else {
node = stack.pop();
node = node.rightChild;
}
}
}
// 中序遍历的非递归实现
public static void nonRecInOrder(TreeNode subTree) {
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode node = subTree;
while (node != null || stack.size() > 0) {
// 存在左子树
if (node != null) {
stack.push(node);
node = node.leftChild;
}
else {
node = stack.pop();
visted(node);
node = node.rightChild;
}
}
}
// 后序遍历的非递归实现
public static void nonRecPostOrder(TreeNode subTree) {
if (null == subTree) { //为确保下面循环至少执行一次
return;
}
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode node = subTree;
TreeNode lastVisited = subTree;
while (true) {
// 左路入栈
while (node.leftChild != null) {
stack.push(node); //第一次压栈, 为了访问左路后退出
node = node.leftChild;
}
// 连续处理从右路返回的节点
while (node.rightChild == null || node.rightChild == lastVisited) {
// 访问并纪录本次访问节点
visted(node);
lastVisited = node;
if (stack.empty()) {
return;
}
node = stack.pop();
}
// 处理从左路返回的节点
stack.push(node); // 第二次压栈, 为了访问右路后退出
node = node.rightChild;
}
}
}
// 二叉搜索树
public void add(int data) {
add(root, data);
}
public boolean contains(int data) {
return contains(root, data);
}
public int minValue() {
return findMin(root).data;
}
public int maxValue() {
return findMax(root).data;
}
private TreeNode findMin(TreeNode subTree) {
if (null == subTree) {
return null;
} else if (null == subTree.leftChild) {
return subTree;
}
return findMin(subTree.leftChild);
}
private TreeNode findMax(TreeNode subTree) {
if (null != subTree) {
while (null != subTree.rightChild) {
subTree = subTree.rightChild;
}
}
return subTree;
}
// 添加节点进搜索树
private TreeNode add(TreeNode subTree, int data) {
if (null == subTree) {
return new TreeNode(data);
} else if (data > subTree.data) {
subTree.rightChild = add(subTree.rightChild, data);
return subTree;
} else if (data < subTree.data) {
subTree.leftChild = add(subTree.leftChild, data);
return subTree;
} // 这里限定搜索树中元素不重复
return subTree;
}
private boolean contains(TreeNode subTree, int data) {
if (null == subTree) {
return false;
} else if (data > subTree.data) {
return contains(subTree.rightChild, data);
} else if (data < subTree.data){
return contains(subTree.leftChild, data);
} else {
return true;
}
}
private TreeNode remove(TreeNode subTree, int data) {
if (null == subTree) {
return null;
} else if (data > subTree.data) {
return remove(subTree.rightChild, data);
} else if (data < subTree.data) {
return remove(subTree.leftChild, data);
} else if (null == subTree.leftChild || null == subTree.rightChild) { //节点匹配, 只有一个孩子或没有孩子
return (subTree.leftChild != null) ? subTree.leftChild : subTree.rightChild;
} else { //节点匹配, 有两个孩子
subTree.data = findMin(subTree.rightChild).data;
subTree.rightChild = remove(subTree.rightChild, subTree.data);
return subTree;
}
}
// 测试
public static void main(String[] args) {
// 创建树
int[] values = new int[8];
for (int i = 0; i < 8; i++) {
int num = (int) (Math.random() * 15);
if (!checkDup(values, num))
values[i] = num;
else
i--;
}
System.out.println("generate Nums:" + Arrays.toString(values));
BSTree tree = new BSTree(new TreeNode(values[0]));
for (int i = 1; i < values.length; i++) {
tree.add(values[i]);
}
System.out.println("树高: " + TreeNode.height(tree.getRoot()));
System.out.println("树大小: " + TreeNode.size(tree.getRoot()));
System.out.println("前序遍历:");
TreeNode.nonRecPreOrder(tree.getRoot());
System.out.println("中序遍历:");
TreeNode.nonRecInOrder(tree.getRoot());
System.out.println("后序遍历:");
TreeNode.nonRecPostOrder(tree.getRoot());
}
private static boolean checkDup(int[] arr, int value) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value)
return true;
}
return false;
}
}
以上是 二叉树的java实现 的全部内容, 来源链接: utcz.com/z/391130.html