为表达式 -(a + b) * (c + d) - (a + b + c) 构造四元组、三元组和间接三元组
解决方案
首先,该语句将转换为三个地址代码为 -
t1 = a + b
t2 = -t1
t3 = c + d
t4 = t2 * t3
t5 = t1 + c
t6 = t4 - t5
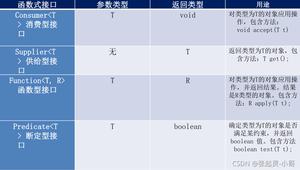
四人间
| 地点 | 运算符 | 参数 1 | 参数 2 | 结果 |
|---|---|---|---|---|
| (0) | + | a | b | t1 |
| (1) | - | t1 | t2 | |
| (2) | + | c | d | t3 |
| (3) | * | t2 | t3 | t4 |
| (4) | + | t1 | C | t5 |
| (5) | - | t4 | t5 | t6 |
三倍
| 地点 | 运算符 | arg 1 | 参数 2 |
| (0) | + | a | b |
| (1) | - | (0) | |
| (2) | + | c | d |
| (3) | * | (1) | (2) |
| (4) | + | (0) | C |
| (5) | - | (3) | (4) |
数组表示
Quadruple 是一种结构,最多包含四个字段,即 operator、Argument 1、Argument 2 和 Result。三元组有三个字段来表示三个地址代码。三元组的字段包括运算符的名称、第一个源操作数和第二个源操作数。
这种三地址代码表示包含三(3)个字段,即,一个用于运算符,两个用于参数(即,参数 1 和参数 2)。在此表示中,不使用临时变量。我们不使用临时变量,而是使用括号中的数字来表示指向符号表特定记录的指针。
四倍和三倍会导致一些内存浪费,因为某些字段没有被占用。为了防止浪费空间,表达式可以用一个数组表示。
示例- 考虑一个语句
a = -b + c * d
它的三个地址代码将是
t1 = -b
t2 = c * d
t3 = t1 + t2
a = t3
四倍将是
| Location | 运算符 | arg 1 | 参数 2 | Result |
| (0) | - | b | t1 | |
| (1) | * | c | d | t2 |
| (2) | + | t1 | t2 | t3 |
| (3) | = | t3 | A |
由于 Quadruple 中存在空间浪费,因此可以将其转换为 Array Representation 为
| - | 乙 | t1 | * | C | d | t2 | + | t1 | t2 | t3 | = | t3 | 一种 |
优势
它节省了内存空间。
坏处
它不能识别一个词,即它是一个运算符还是一个操作数。在 Quadruple 中,它可以快速完成,因为运算符和操作数都写在相应的字段中。
以上是 为表达式 -(a + b) * (c + d) - (a + b + c) 构造四元组、三元组和间接三元组 的全部内容, 来源链接: utcz.com/z/363440.html