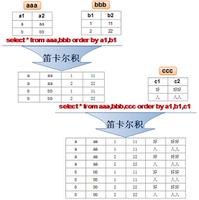
证明有限个可数集的笛卡尔积是可数的？

我们必须证明有限个可数集的笛卡尔积是可数的。

令 X1, X2 ,…….. Xn 为可数集。

Yk= X1 * X2 * …….* 当 k =1 时，Xk ……。否）。因此，

Yn := X1 * X2 * · · · * Xn

证明

使用归纳 -

如果 k = 1，则 Y1 = X1 是可数的。

假设Yk (k ∈ n, 1 ≤ k < n) 是可数的；

那么 Yk+1 = ( X1 * X2 * …….* Xk) * Xk+1 = Yk * Xk+1 其中 Yk 和 Xk+1 可以称为可数的。因此可数集的笛卡尔积总是可数的。所以，Yk+1 是可数的。

同样，让我们证明有限个可数无限集的笛卡尔积是可数无限的。

证明

令 X1, X2 ,…….. Xn 为可数无穷集。

定义 Yk= X1 * X2 * …….* Xk 当 k =1……。否）。因此

因此，Yn := X1 * X2 * · · · * Xn

首先我们需要证明 Yn 是可数的。

通过归纳法

如果 k=1，则集合 Y1=X1 是可数无穷大的。

假设 Yk( K☐N, 1<=K<N) 是可数无穷大。

然后，

Yk+1=(X1 * X2 *....Xk) * Xk+1

Yk+1=Yk * Xk+1

其中，Yk 和 Xk+1 都是可数无穷大，我们知道可数集的笛卡尔积是可数的。

因此，Yk+1 是可数无穷大。

我们得出结论，X1 * X2 *.....Xn 是可数无限的。

因此，有限个可数无限集的笛卡尔积是可数无限的。