最短路径的 Bellman-Ford 算法

Z时代
2024-01-10
分类：综合

Bellman-Ford 算法用于找到从源顶点到任何其他顶点的最小距离。该算法与 Dijkstra 算法的主要区别在于，在 Dijkstra 算法中我们无法处理负权重，但在这里我们可以轻松处理。

Bellman-Ford 算法以自下而上的方式找到距离。首先，它找到路径中只有一条边的那些距离。之后增加路径长度以找到所有可能的解决方案。

输入和输出

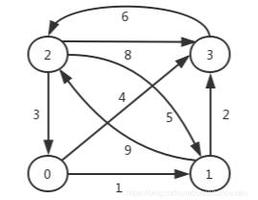
Input:

The cost matrix of the graph:

0 6 ∞ 7 ∞

∞ 0 5 8 -4

∞ -2 0 ∞ ∞

∞ ∞ -3 0 9

2 ∞ 7 ∞ 0

Output:

源顶点： 2

Vert: 0 1 2 3 4

Dist: -4 -2 0 3 -6

Pred: 4 2 -1 0 1

The graph has no negative edge cycle

算法

bellmanFord(dist, pred, source)

输入 -距离列表、前驱列表和源顶点。
输出 -当发现负循环时为真。

Begin
   iCount := 1
   maxEdge := n * (n - 1) / 2     //n 是顶点数
   for all vertices v of the graph, do
      dist[v] := ∞
      pred[v] := ϕ
   done
   dist[source] := 0
   eCount := number of edges present in the graph
   create edge list named edgeList
   while iCount < n, do
      for i := 0 to eCount, do
         if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) pred[edgeList[i].v] := edgeList[i].u
      done
   done
   iCount := iCount + 1
   for all vertices i in the graph, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i),
         then return true
   done
   return false
End

示例

#include<iostream>
#include<iomanip>
#define V 5
#define INF 999
using namespace std;
//图（有向）顶点 5 的成本矩阵
int costMat[V][V] = {
   {0, 6, INF, 7, INF},
   {INF, 0, 5, 8, -4},
   {INF, -2, 0, INF, INF},
   {INF, INF, -3, 0, 9},
   {2, INF, 7, INF, 0}
};
typedef struct {
   int u, v, cost;
}edge;
int isDiagraph() {
   //检查图是否为有向图
   int i, j;
   for(i = 0; i<V; i++) {
      for(j = 0; j<V; j++) {
         if(costMat[i][j] != costMat[j][i]) {
            return 1;      //图是有向的
         }
      }
   }
   return 0;//图是无向的
}
int makeEdgeList(edge *eList) {
   //从图的边创建边列表
   int count = -1;
   if(isDiagraph()) {
      for(int i = 0; i<V; i++) {
         for(int j = 0; j<V; j++) {
            if(costMat[i][j] != 0 && costMat[i][j] != INF) {
               count++;         //当图有向时找到边
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }else {
      for(int i = 0; i<V; i++) {
         for(int j = 0; j<i; j++) {
            if(costMat[i][j] != INF) {
               count++;         //图无向时的边查找
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }
   return count+1;
}
int bellmanFord(int *dist, int *pred,int src) {
   int icount = 1, ecount, max = V*(V-1)/2;
   edge edgeList[max];
   for(int i = 0; i<V; i++) {
      dist[i] = INF;      //初始化为无穷大
      pred[i] = -1;      //没有找到前任。
   }
   dist[src] = 0;//对于起始顶点，距离为 0
   ecount = makeEdgeList(edgeList);       //边列表形成
   while(icount < V) {       //迭代次数为 (Vertex - 1)
      for(int i = 0; i<ecount; i++) {
         if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {      //放松边缘并设置前任
            dist[edgeList[i].v] = dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v];
            pred[edgeList[i].v] = edgeList[i].u;
         }
      }
      icount++;
   }
   //负循环测试
   for(int i = 0; i<ecount; i++) {
      if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {
         return 1;    //表示图形有负循环
      }
   }
   return 0;     //无负循环
}
void display(int *dist, int *pred) {
   cout << "Vert: ";
   for(int i = 0; i<V; i++)
      cout <<setw(3) << i << " ";
   cout << endl;
   cout << "Dist: ";
   for(int i = 0; i<V; i++)
      cout << setw(3) << dist[i] << " ";
   cout << endl;
   cout << "Pred: ";
   for(int i = 0; i<V; i++)
      cout << setw(3) << pred[i] << " ";
   cout << endl;
}
int main() {
   int dist[V], pred[V], source, report;
   source = 2;
   report = bellmanFord(dist, pred, source);
   cout << "源顶点： " << source<<endl;
   display(dist, pred);
   if(report)
      cout << "The graph has a negative edge cycle" << endl;
   else
      cout << "The graph has no negative edge cycle" << endl;
}

输出结果