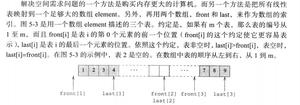
什么是数据转换？

在数据转换中，数据被转换或组合成适合挖掘的形式。数据转换可能涉及以下内容 -

平滑- 它可以消除数据中的噪声。此类方法包括分箱、回归和聚类。

聚合- 在聚合中，汇总或聚合操作应用于数据。例如，可以汇总每日销售数据以计算每月和每年的总金额。该阶段通常用于制作数据立方体，用于多粒度数据的分析。

泛化- 在泛化中，低级或“原始”（原始）数据通过使用概念层次结构由更高级的概念恢复。例如，分类属性（例如街道）可以推广到更大级别的概念，例如城市或国家/地区。同样，数字属性（例如年龄）的值可以映射到更大级别的概念，例如青年、中年和高级。

归一化- 在归一化中，属性数据被缩放到一个小的指定范围内，例如 -1.0 到 1.0，或 0.0 到 1.0。

属性构建- 在属性构建中，从给定的属性集中开发和添加新属性以促进挖掘过程。

平滑是一种数据清理形式，在用户指定转换以纠正数据不一致的数据清理过程中得到解决。聚合和泛化作为数据缩减的形式提供。属性通过缩放其值来标准化，以便它们在一个小的指定顺序内下降，包括 0.0 到 1.0。

归一化对于包含神经网络的分类算法或最近邻分类和聚类等距离测量特别有用。如果使用神经网络反向传播算法进行分类挖掘，对训练元组中测量的每个属性的输入值进行归一化将有助于加快学习阶段。

对于基于距离的方法，归一化有助于防止初始范围较大的属性（例如收入）超过初始范围较小的属性（例如二元属性）。数据归一化的方法有很多，如下所示 -

Min-max normalization - 它对原始数据进行线性变换。假设 min _A和 max _A是属性_A的最小值和最大值。 Min-max 归一化通过计算将 A 的值 v 映射到[new_min _A , new_max _A ]范围内的v ^'

$$v'=\frac{v-min_{A}}{max_{A}-min_{A}}(new\_max_{A}- new\_min_{A})+new\_min_{A}$$

Z 分数归一化- 在 z 分数归一化（或零均值归一化）中，属性 A 的值根据 A 的均值和标准差进行归一化。 A 的值 v 归一化为 v ^'通过计算

$$v'=\frac{vA^{'}}{\sigma_{A}}$$

其中 A 和 σ _A分别是属性 A 的均值和标准差。当属性 A 的实际最小值和最大值未知时，或者当存在支配最小值-最大值归一化的异常值时，这种归一化方法很有用。

十进制缩放- 十进制缩放归一化通过更改属性 A 的值的小数点进行归一化。根据 A 的最大绝对值移动的小数点数。A 的值 v通过计算归一化为 v ^′

$$v'=\frac{v}{10^{j}}$$

其中 j 是满足 Max (|v ^′ |)<1的最小整数。