java实现 二叉搜索树功能
一、概念
二叉搜索树也成二叉排序树,它有这么一个特点,某个节点,若其有两个子节点,则一定满足,左子节点值一定小于该节点值,右子节点值一定大于该节点值,对于非基本类型的比较,可以实现Comparator接口,在本文中为了方便,采用了int类型数据进行操作。
要想实现一颗二叉树,肯定得从它的增加说起,只有把树构建出来了,才能使用其他操作。
二、二叉搜索树构建
谈起二叉树的增加,肯定先得构建一个表示节点的类,该节点的类,有这么几个属性,节点的值,节点的父节点、左节点、右节点这四个属性,代码如下
static class Node{
Node parent;
Node leftChild;
Node rightChild;
int val;
public Node(Node parent, Node leftChild, Node rightChild,int val) {
super();
this.parent = parent;
this.leftChild = leftChild;
this.rightChild = rightChild;
this.val = val;
}
public Node(int val){
this(null,null,null,val);
}
public Node(Node node,int val){
this(node,null,null,val);
}
}
这里采用的是内部类的写法,构建完节点值后,再对整棵树去构建,一棵树,先得有根节点,再能延伸到余下子节点,那在这棵树里,也有一些属性,比如基本的根节点root,树中元素大小size,这两个属性,如果采用了泛型,可能还得增加Comparator属性,或提供其一个默认实现。具体代码如下
public class SearchBinaryTree {
private Node root;
private int size;
public SearchBinaryTree() {
super();
}
}
三、增加
当要进行添加元素的时候,得考虑根节点的初始化,一般情况有两种、当该类的构造函数一初始化就对根节点root进行初始化,第二种、在进行第一次添加元素的时候,对根节点进行添加。理论上两个都可以行得通,但通常采用的是第二种懒加载形式。
在进行添加元素的时候,有这样几种情况需要考虑
一、添加时判断root是否初始化,若没初始化,则初始化,将该值赋给根节点,size加一。
二、因为二叉树搜索树满足根节点值大于左节点,小于右节点,需要将插入的值,先同根节点比较,若大,则往右子树中进行查找,若小,则往左子树中进行查找。直到某个子节点。
这里的插入实现,可以采用两种,一、递归、二、迭代(即通过while循环模式)。
3.1、递归版本插入
public boolean add(int val){
if(root == null){
root = new Node(val);
size++;
return true;
}
Node node = getAdapterNode(root, val);
Node newNode = new Node(val);
if(node.val > val){
node.leftChild = newNode;
newNode.parent = node;
}else if(node.val < val){
node.rightChild = newNode;
newNode.parent = node;
}else{
// 暂不做处理
}
size++;19 return true;
}
/**
* 获取要插入的节点的父节点,该父节点满足以下几种状态之一
* 1、父节点为子节点
* 2、插入节点值比父节点小,但父节点没有左子节点
* 3、插入节点值比父节点大,但父节点没有右子节点
* 4、插入节点值和父节点相等。
* 5、父节点为空
* 如果满足以上5种情况之一,则递归停止。
* @param node
* @param val
* @return
*/
private Node getAdapterNode(Node node,int val){
if(node == null){
return node;
}
// 往左子树中插入,但没左子树,则返回
if(node.val > val && node.leftChild == null){
return node;
}
// 往右子树中插入,但没右子树,也返回
if(node.val < val && node.rightChild == null){
return node;
}
// 该节点是叶子节点,则返回
if(node.leftChild == null && node.rightChild == null){
return node;
}
if(node.val > val && node.leftChild != null){
return getAdaptarNode(node.leftChild, val);
}else if(node.val < val && node.rightChild != null){
return getAdaptarNode(node.rightChild, val);
}else{
return node;
}
}
使用递归,先找到递归的结束点,再去把整个问题化为子问题,在上述代码里,逻辑大致是这样的,先判断根节点有没有初始化,没初始化则初始化,完成后返回,之后通过一个函数去获取适配的节点。之后进行插入值。
3.2、迭代版本
public boolean put(int val){
return putVal(root,val);
}
private boolean putVal(Node node,int val){
if(node == null){// 初始化根节点
node = new Node(val);
root = node;
size++;
return true;
}
Node temp = node;
Node p;
int t;
/**
* 通过do while循环迭代获取最佳节点,
*/
do{
p = temp;
t = temp.val-val;
if(t > 0){
temp = temp.leftChild;
}else if(t < 0){
temp = temp.rightChild;
}else{
temp.val = val;
return false;
}
}while(temp != null);
Node newNode = new Node(p, val);
if(t > 0){
p.leftChild = newNode;
}else if(t < 0){
p.rightChild = newNode;
}
size++;
return true;
}
原理其实和递归一样,都是获取最佳节点,在该节点上进行操作。
论起性能,肯定迭代版本最佳,所以一般情况下,都是选择迭代版本进行操作数据。
四、删除
可以说在二叉搜索树的操作中,删除是最复杂的,要考虑的情况也相对多,在常规思路中,删除二叉搜索树的某一个节点,肯定会想到以下四种情况,
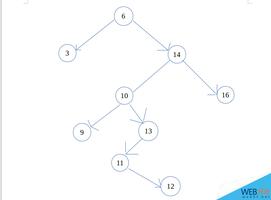
1、要删除的节点没有左右子节点,如上图的D、E、G节点
2、要删除的节点只有左子节点,如B节点
3、要删除的节点只有右子节点,如F节点
4、要删除的节点既有左子节点,又有右子节点,如 A、C节点
对于前面三种情况,可以说是比较简单,第四种复杂了。下面先来分析第一种
若是这种情况,比如 删除D节点,则可以将B节点的左子节点设置为null,若删除G节点,则可将F节点的右子节点设置为null。具体要设置哪一边,看删除的节点位于哪一边。
第二种,删除B节点,则只需将A节点的左节点设置成D节点,将D节点的父节点设置成A即可。具体设置哪一边,也是看删除的节点位于父节点的哪一边。
第三种,同第二种。
第四种,也就是之前说的有点复杂,比如要删除C节点,将F节点的父节点设置成A节点,F节点左节点设置成E节点,将A的右节点设置成F,E的父节点设置F节点(也就是将F节点替换C节点),还有一种,直接将E节点替换C节点。那采用哪一种呢,如果删除节点为根节点,又该怎么删除?
对于第四种情况,可以这样想,找到C或者A节点的后继节点,删除后继节点,且将后继节点的值设置为C或A节点的值。先来补充下后继节点的概念。
一个节点在整棵树中的后继节点必满足,大于该节点值得所有节点集合中值最小的那个节点,即为后继节点,当然,也有可能不存在后继节点。
但是对于第四种情况,后继节点一定存在,且一定在其右子树中,而且还满足,只有一个子节点或者没有子节点两者情况之一。具体原因可以这样想,因为后继节点要比C节点大,又因为C节点左右子节一定存在,所以一定存在右子树中的左子节点中。就比如C的后继节点是F,A的后继节点是E。
有了以上分析,那么实现也比较简单了,代码如下
public boolean delete(int val){
Node node = getNode(val);
if(node == null){
return false;
}
Node parent = node.parent;
Node leftChild = node.leftChild;
Node rightChild = node.rightChild;
//以下所有父节点为空的情况,则表明删除的节点是根节点
if(leftChild == null && rightChild == null){//没有子节点
if(parent != null){
if(parent.leftChild == node){
parent.leftChild = null;
}else if(parent.rightChild == node){
parent.rightChild = null;
}
}else{//不存在父节点,则表明删除节点为根节点
root = null;
}
node = null;
return true;
}else if(leftChild == null && rightChild != null){// 只有右节点
if(parent != null && parent.val > val){// 存在父节点,且node位置为父节点的左边
parent.leftChild = rightChild;
}else if(parent != null && parent.val < val){// 存在父节点,且node位置为父节点的右边
parent.rightChild = rightChild;
}else{
root = rightChild;
}
node = null;
return true;
}else if(leftChild != null && rightChild == null){// 只有左节点
if(parent != null && parent.val > val){// 存在父节点,且node位置为父节点的左边
parent.leftChild = leftChild;
}else if(parent != null && parent.val < val){// 存在父节点,且node位置为父节点的右边
parent.rightChild = leftChild;
}else{
root = leftChild;
}
return true;
}else if(leftChild != null && rightChild != null){// 两个子节点都存在
Node successor = getSuccessor(node);// 这种情况,一定存在后继节点
int temp = successor.val;
boolean delete = delete(temp);
if(delete){
node.val = temp;
}
successor = null;
return true;
}
return false;
}
/**
* 找到node节点的后继节点
* 1、先判断该节点有没有右子树,如果有,则从右节点的左子树中寻找后继节点,没有则进行下一步
* 2、查找该节点的父节点,若该父节点的右节点等于该节点,则继续寻找父节点,
* 直至父节点为Null或找到不等于该节点的右节点。
* 理由,后继节点一定比该节点大,若存在右子树,则后继节点一定存在右子树中,这是第一步的理由
* 若不存在右子树,则也可能存在该节点的某个祖父节点(即该节点的父节点,或更上层父节点)的右子树中,
* 对其迭代查找,若有,则返回该节点,没有则返回null
* @param node
* @return
*/
private Node getSuccessor(Node node){
if(node.rightChild != null){
Node rightChild = node.rightChild;
while(rightChild.leftChild != null){
rightChild = rightChild.leftChild;
}
return rightChild;
}
Node parent = node.parent;
while(parent != null && (node == parent.rightChild)){
node = parent;
parent = parent.parent;
}
return parent;
}
具体逻辑,看上面分析,这里不作文字叙述了,
除了这种实现,在算法导论书中,提供了另外一种实现。
public boolean remove(int val){
Node node = getNode(val);
if(node == null){
return false;
}
if(node.leftChild == null){// 1、左节点不存在,右节点可能存在,包含两种情况 ,两个节点都不存在和只存在右节点
transplant(node, node.rightChild);
}else if(node.rightChild == null){//2、左孩子存在,右节点不存在
transplant(node, node.leftChild);
}else{// 3、两个节点都存在
Node successor = getSuccessor(node);// 得到node后继节点
if(successor.parent != node){// 后继节点存在node的右子树中。
transplant(successor, successor.rightChild);// 用后继节点的右子节点替换该后继节点
successor.rightChild = node.rightChild;// 将node节点的右子树赋给后继节点的右节点,即类似后继与node节点调换位置
successor.rightChild.parent = successor;// 接着上一步 给接过来的右节点的父引用复制
}
transplant(node, successor);
successor.leftChild = node.leftChild;
successor.leftChild.parent = successor;
}
return true;
}
/**
* 将child节点替换node节点
* @param root 根节点
* @param node 要删除的节点
* @param child node节点的子节点
*/
private void transplant(Node node,Node child){
/**
* 1、先判断 node是否存在父节点
* 1、不存在,则child替换为根节点
* 2、存在,则继续下一步
* 2、判断node节点是父节点的那个孩子(即判断出 node是右节点还是左节点),
* 得出结果后,将child节点替换node节点 ,即若node节点是左节点 则child替换后 也为左节点,否则为右节点
* 3、将node节点的父节点置为child节点的父节点
*/
if(node.parent == null){
this.root = child;
}else if(node.parent.leftChild == node){
node.parent.leftChild = child;
}else if(node.parent.rightChild == node){
node.parent.rightChild = child;
}
if(child != null){
child.parent = node.parent;
}
}
五、查找
查找也比较简单,其实在增加的时候,已经实现了。实际情况中,这部分可以抽出来单独方法。代码如下
public Node getNode(int val){
Node temp = root;
int t;
do{
t = temp.val-val;
if(t > 0){
temp = temp.leftChild;
}else if(t < 0){
temp = temp.rightChild;
}else{
return temp;
}
}while(temp != null);
return null;
}
六、二叉搜索树遍历
在了解二叉搜索树的性质后,很清楚的知道,它的中序遍历是从小到大依次排列的,这里提供中序遍历代码
public void print(){
print(root);
}
private void print(Node root){
if(root != null){
print(root.leftChild);
System.out.println(root.val);// 位置在中间,则中序,若在前面,则为先序,否则为后续
print(root.rightChild);
}
}
总结
以上所述是小编给大家介绍的java实现 二叉搜索树功能,希望对大家有所帮助,如果大家有任何疑问欢迎给我留言,小编会及时回复大家的!
以上是 java实现 二叉搜索树功能 的全部内容, 来源链接: utcz.com/z/350976.html