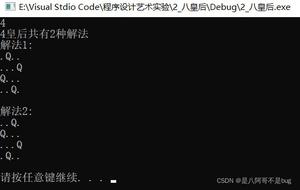
八皇后问题的相关C++代码解答示例
八皇后问题即指在一个8*8的棋盘上放置8个皇后,不允许任何两个皇后在棋盘的同一行、同一列和同一对角线上。关键字:递归、上溯.通用技巧:
经观察发现,对8 x 8的二维数组上的某点a[i][j](0<=i,j<=7)
其主对角线(即左上至右下)上的每个点的i-j+7的值(范围在(0,14))均相等;
其从对角线(即右上至左下)上的每个点的i+j的值(范围在(0,14))均相等;
且每个主对角线之间的i-j+7的值均不同,每个从对角线之间的i-j+7的值亦不同;
如a[3][4]:
主:3-4+7=6
从:3+4=7
因此可设两个数组b[15],c[15]分别表示主、从对角线是否安全
(为1表示有皇后,不安全;为0表示安全)
每行有且仅有一个皇后:
每i个皇后放在每i行(0<=i<=7)
void eightQueens( int line );
题目描述:
会下国际象棋的人都很清楚:皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上(有8 * 8个方格),使它们谁也不能被吃掉!这就是著名的八皇后问题。
对于某个满足要求的8皇后的摆放方法,定义一个皇后串a与之对应,即a=b1b2...b8,其中bi为相应摆法中第i行皇后所处的列数。已经知道8皇后问题一共有92组解(即92个不同的皇后串)。
给出一个数b,要求输出第b个串。串的比较是这样的:皇后串x置于皇后串y之前,当且仅当将x视为整数时比y小。
输入:
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数b(1 <= b <= 92)
输出:
输出有n行,每行输出对应一个输入。输出应是一个正整数,是对应于b的皇后串。
样例输入:
2
1
92
样例输出:
15863724
84136275
思路
先贴出一个可以ac的摆放位置出来,防止大家连国际象棋棋盘的样子都不清楚。
由于八个皇后不能处在同一行,那么可以肯定每个皇后占据一行。我们可以先定义一个数组column[9],数组中的第i个数字表示位于第i行皇后的列号(因为数组下标从0开始,因此这里想表示1-8需要申请9个整型的数据空间)。
先把column数组初始化为1-8,忽略开始的第一个元素
接下来,对column做无重复的全排列,因为我们使用不同的数字对column进行初始化,所以八皇后肯定在不同的列。
接下来,我们只需要判断八皇后是否在同一对角线即可,学过数学的都知道,可以表示为y = x + b 或者 y = -x + b
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define EIGHT 8
struct result
{
int total;
int num[10];
};
int wzyindex, column[10];
struct result results[100];
/**
* Description:预处理八皇后的下标数组
*/
void pre_prosess(int n)
{
int i;
for (i = 1; i <= n; i ++) {
column[i] = i;
}
}
/**
* Description:column数组数字交换
*/
void swap(int begin, int k)
{
int temp;
temp = column[begin];
column[begin] = column[k];
column[k] = temp;
}
/**
* Description:防止全排列出现重复数据
*/
int check_swap(int begin, int k)
{
int i;
for (i = begin; i < k; i ++) {
if (column[i] == column[k]) {
return 0;
}
}
return 1;
}
int is_eightqueue(int n)
{
int i, j;
for (i = 1; i <= n; i ++) {
for (j = i + 1; j <= n; j ++) {
if (i - j == column[i] - column[j] || i - j == column[j] - column[i])
return 0;
}
}
return 1;
}
void permutation_queue(int begin, int end)
{
int k, total;
if (begin == end) { // 检查八皇后排列正确性
if (is_eightqueue(end)) {
for (k = 1, total = 0; k <= end; k ++) {
total = 10 * total + column[k];
results[wzyindex].num[k] = column[k];
}
results[wzyindex].total = total;
wzyindex ++;
}
} else { // 全排列
for (k = begin; k <= end; k ++) {
if (check_swap(begin, k)) { // 保证无重复的全排列
swap(begin, k);
permutation_queue(begin + 1, end);
swap(begin, k);
}
}
}
}
int compare(const void *p, const void *q)
{
const struct result *a = p;
const struct result *b = q;
return a->total - b->total;
}
int main()
{
int i, n, m;
pre_prosess(EIGHT);
wzyindex = 0;
permutation_queue(1, EIGHT);
qsort(results, wzyindex, sizeof(results[0]), compare);
while (scanf("%d", &n) != EOF) {
while (n --) {
scanf("%d", &m);
m -= 1;
for (i = 1; i <= EIGHT; i ++) {
printf("%d", results[m].num[i]);
}
printf("\n");
}
}
return 0;
}
/**************************************************************
Problem: 1140
User: wangzhengyi
Language: C
Result: Accepted
Time:10 ms
Memory:916 kb
****************************************************************/
dfs思路
其实就是dfs挨层遍历,找出所有符合要求的组合,直接上ac代码
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#define N 8
typedef struct point {
int x, y;
} point;
point pts[N];
typedef struct string {
char str[N + 1];
} string;
string strs[93];
int windex, count;
int isOk(int x, int y)
{
int i, flag = 1;
for (i = 0; i < count; i ++) {
if (pts[i].y == y || abs(y - pts[i].y) == abs(x - pts[i].x)) {
flag = 0;
break;
}
}
return flag;
}
void bfsEight(int level)
{
int i;
if (level > N) {
for (i = 0; i < N; i ++) {
strs[windex].str[i] = pts[i].y + '0';
}
strs[windex].str[i] = '\0';
windex ++;
} else {
point t;
for (i = 1; i <= N; i ++) {
t.x = level;
t.y = i;
if (isOk(t.x, t.y)) {
pts[count ++] = t;
bfsEight(level + 1);
count -= 1;
}
}
}
}
int cmp(const void *p, const void *q)
{
const string *a = p;
const string *b = q;
return strcmp(a->str, b->str);
}
int main(void)
{
int n, num;
count = windex = 0;
bfsEight(1);
qsort(strs, count, sizeof(strs[0]), cmp);
scanf("%d", &n);
while (n --) {
scanf("%d", &num);
printf("%s\n", strs[num - 1].str);
}
return 0;
}
/**************************************************************
Problem: 1140
User: wangzhengyi
Language: C
Result: Accepted
Time:10 ms
Memory:916 kb
****************************************************************/
以上是 八皇后问题的相关C++代码解答示例 的全部内容, 来源链接: utcz.com/z/348607.html