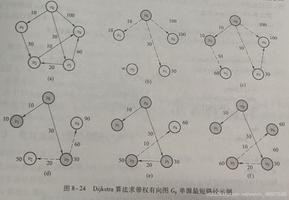
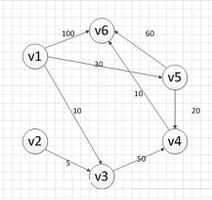
Dijkstra最短路径算法

Z时代
2024-01-10
分类：综合

主要问题与上一个相同，从起始节点到任何其他节点，找到最小的距离。在此问题中，主要区别在于该图是使用邻接矩阵表示的。（为此目的，成本矩阵和邻接矩阵相似）。

对于邻接表表示，时间复杂度为O（V ^ 2），其中V是图形G(V,E)中的节点数

输入输出

Input:

The adjacency matrix:Output:

0 to 1, Using: 0, Cost: 3

0 to 2, Using: 1, Cost: 5

0 to 3, Using: 1, Cost: 4

0 to 4, Using: 3, Cost: 6

0 to 5, Using: 2, Cost: 7

0 to 6, Using: 4, Cost: 7

算法

dijkstraShortestPath(n, dist, next, start)

输入-节点总数n，每个顶点的距离列表，存储下一个节点的下一个列表以及种子或起始顶点。

输出- 从起点到所有其他顶点的最短路径。

Begin
   create a status list to hold the current status of the selected node
   for all vertices u in V do
      status[u] := unconsidered
      dist[u] := distance from source using cost matrix
      next[u] := start
   done
   status[start] := considered, dist[start] := 0 and next[start] := φ
   while take unconsidered vertex u as distance is minimum do
      status[u] := considered
      for all vertex v in V do
         if status[v] = unconsidered then
            if dist[v] > dist[u] + cost[u,v] then
               dist[v] := dist[u] + cost[u,v]
               next[v] := u
      done
   done
End

示例

#include<iostream>
#define V 7
#define INF 999
using namespace std;
//图的成本矩阵
int costMat[V][V] = {
   {0, 3, 6, INF, INF, INF, INF},
   {3, 0, 2, 1, INF, INF, INF},
   {6, 2, 0, 1, 4, 2, INF},
   {INF, 1, 1, 0, 2, INF, 4},
   {INF, INF, 4, 2, 0, 2, 1},
   {INF, INF, 2, INF, 2, 0, 1},
   {INF, INF, INF, 4, 1, 1, 0}
};
int minimum(int *status, int *dis, int n) {
   int i, min, index;
   min = INF;
   for(i = 0; i<n; i++)
      if(dis[i] < min && status[i] == 1) {
         min = dis[i];
         index = i;
      }
   if(status[index] == 1)
      return index; //minimum unconsidered vertex distance
   else
      return -1;    //when all vertices considered
}
void dijkstra(int n, int *dist,int *next, int s) {
   int status[V];
   int u, v;
   //初始化
   for(u = 0; u<n; u++) {
      status[u] = 1;               //unconsidered vertex
      dist[u] = costMat[u][s];     //distance from source
      next[u] = s;
   }
   //对于源顶点
   status[s] = 2; dist[s] = 0; next[s] = -1; //-1 for starting vertex
   while((u = minimum(status, dist, n)) > -1) {
      status[u] = 2;//now considered
      for(v = 0; v<n; v++)
         if(status[v] == 1)
            if(dist[v] > dist[u] + costMat[u][v]) {
               dist[v] = dist[u] + costMat[u][v];   //update distance
               next[v] = u;
            }
   }
}
main() {
   int dis[V], next[V], i, start = 0;
   dijkstra(V, dis, next, start);
   for(i = 0; i<V; i++)
      if(i != start)
         cout << start << " to " << i <<", Using: " << next[i] << ",
   Cost: " << dis[i] << endl;
}