有向无环图中的最短路径
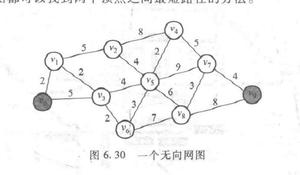
给出了一个加权有向无环图。还提供了另一个源顶点。现在,我们必须在图中找到从起始节点到所有其他顶点的最短距离。
为了检测较小的距离,我们可以对负负图使用另一种算法,例如Bellman-Ford,对于正负数,Dijkstra算法也很有帮助。在这里,对于有向无环图,我们将使用拓扑排序技术来降低复杂度。
输入输出
Input:The cost matrix of the graph.
0 5 3 -∞ -∞ -∞
-∞ 0 2 6 -∞ -∞
-∞ -∞ 0 7 4 2
-∞ -∞ -∞ 0 -1 1
-∞ -∞ -∞ -∞ 0 -2
-∞ -∞ -∞ -∞ -∞ 0
Output:
Shortest Distance from Source Vertex 1
Infinity 0 2 6 5 3
算法
topoSort(u,已访问,堆栈)
输入:起始节点u,要跟踪的访问列表,堆栈。
输出:以拓扑方式对节点进行排序。
Beginmark u as visited
for all vertex v, which is connected with u, do
if v is not visited, then
topoSort(v, visited, stack)
done
push u into the stack
End
shortestPath(开始)
输入-起始节点。
输出-距起始节点的所有顶点的最短距离的列表。
Begininitially make all nodes as unvisited
for each node i, in the graph, do
if i is not visited, then
topoSort(i, visited, stack)
done
make distance of all vertices as ∞
dist[start] := 0
while stack is not empty, do
pop stack item and take into nextVert
if dist[nextVert] ≠∞, then
for each vertices v, which is adjacent with nextVert, do
if cost[nextVert, v] ≠∞, then
if dist[v] > dist[nectVert] + cost[nextVert, v], then
dist[v] := dist[nectVert] + cost[nextVert, v]
done
done
for all vertices i in the graph, do
if dist[i] = ∞, then
display Infinity
else
display dist[i]
done
End
示例
#include<iostream>#include<stack>
#define NODE 6
#define INF 9999
using namespace std;
int cost[NODE][NODE] = {
{0, 5, 3, INF, INF, INF},
{INF, 0, 2, 6, INF, INF},
{INF, INF, 0, 7, 4, 2},
{INF, INF, INF, 0, -1, 1},
{INF, INF, INF, INF, 0, -2},
{INF, INF, INF, INF, INF, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(cost[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void shortestPath(int start) {
stack<int> stk;
int dist[NODE];
bool vis[NODE];
for(int i = 0; i<NODE;i++)
vis[i] = false; // make all nodes as unvisited at first
for(int i = 0; i<NODE; i++) //perform topological sort for vertices
if(!vis[i])
topoSort(i, vis, stk);
for(int i = 0; i<NODE; i++)
dist[i] = INF; //initially all distances are infinity
dist[start] = 0; //distance for start vertex is 0
while(!stk.empty()) { //when stack contains element, process in topological order
int nextVert = stk.top(); stk.pop();
if(dist[nextVert] != INF) {
for(int v = 0; v<NODE; v++) {
if(cost[nextVert][v] && cost[nextVert][v] != INF){ if(dist[v] > dist[nextVert] +cost[nextVert][v])dist[v] = dist[nextVert] + cost[nextVert][v];
}
}
}
for(int i = 0; i<NODE; i++)
(dist[i] == INF)?cout << "Infinity ":cout << dist[i]<<" ";
}
main() {
int start = 1;
cout << "Shortest Distance From Source Vertex "<<start<<endl;
shortestPath(start);
}
输出结果
Shortest Distance From Source Vertex 1Infinity 0 2 6 5 3
以上是 有向无环图中的最短路径 的全部内容, 来源链接: utcz.com/z/337987.html