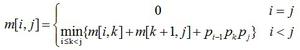使用动态规划解决背包问题的 C++ 程序

• Z时代
• 2024-01-10
• 分类：综合

这是一个使用动态规划解决 0-1 背包问题的 C++ 程序。在 0-1 背包问题中，给出了一组物品，每个物品都有一个重量和一个值。我们需要确定要包含在一个集合中的每个项目的数量，以便总重量小于或等于给定的限制，并且总价值尽可能大。

算法

Begin
Input set of items each with a weight and a value
Set knapsack capacity
Create a function that returns maximum of two integers.
Create a function which returns the maximum value that can be put in a knapsack of capacity W
int knapSack(int W, int w[], int v[], int n)
int i, wt;
int K[n + 1][W + 1]
for i = 0 to n
for wt = 0 to W
if (i == 0 or wt == 0)
   Do K[i][wt] = 0
else if (w[i - 1] <= wt)
   Compute: K[i][wt] = max(v[i - 1] + K[i - 1][wt - w[i - 1]], K[i -1][wt])
else
   K[i][wt] = K[i - 1][wt]
   return K[n][W]
   Call the function and print.
End

示例代码

#include <iostream>
using namespace std;
int max(int x, int y) {
   return (x > y) ? x : y;
}
int knapSack(int W, int w[], int v[], int n) {
   int i, wt;
   int K[n + 1][W + 1];
   for (i = 0; i <= n; i++) {
      for (wt = 0; wt <= W; wt++) {
         if (i == 0 || wt == 0)
         K[i][wt] = 0;
         else if (w[i - 1] <= wt)
            K[i][wt] = max(v[i - 1] + K[i - 1][wt - w[i - 1]], K[i - 1][wt]);
         else
        K[i][wt] = K[i - 1][wt];
      }
   }
   return K[n][W];
}
int main() {
   cout << "输入背包中的物品数量：";
   int n, W;
   cin >> n;
   int v[n], w[n];
   for (int i = 0; i < n; i++) {
      cout << "输入物品的价值和重量 " << i << ":";
      cin >> v[i];
      cin >> w[i];
   }
   cout << "Enter the capacity of knapsack";
   cin >> W;
   cout << knapSack(W, w, v, n);
   return 0;
}

输入背包中的物品数量：4
输入物品的价值和重量 0:10
50
输入物品的价值和重量 1:20
60
输入物品的价值和重量 2:30
70
输入物品的价值和重量 3:40
90
Enter the capacity of knapsack100
40

以上是 使用动态规划解决背包问题的 C++ 程序 的全部内容， 来源链接： utcz.com/z/335630.html