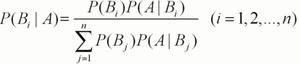Python实现朴素贝叶斯的学习与分类过程解析

Z时代
2024-01-10
分类：综合

概念简介:

朴素贝叶斯基于贝叶斯定理，它假设输入随机变量的特征值是条件独立的，故称之为“朴素”。简单介绍贝叶斯定理：

乍看起来似乎是要求一个概率，还要先得到额外三个概率，有用么？其实这个简单的公式非常贴切人类推理的逻辑，即通过可以观测的数据，推测不可观测的数据。举个例子，也许你在办公室内不知道外面天气是晴天雨天，但是你观测到有同事带了雨伞，那么可以推断外面八成在下雨。

若X 是要输入的随机变量，则Y 是要输出的目标类别。对X 进行分类，即使求的使P(Y|X) 最大的Y值。若X 为n 维特征变量 X = {A1, A2, …..An} ，若输出类别集合为Y = {C1, C2, …. Cm} 。

X 所属最有可能类别 y = argmax P(Y|X), 进行如下推导：

朴素贝叶斯的学习

有公式可知，欲求分类结果，须知如下变量：

各个类别的条件概率，

输入随机变量的特质值的条件概率

示例代码:


import copy
class native_bayes_t:
  def __init__(self, character_vec_, class_vec_):
    """
    构造的时候需要传入特征向量的值，以数组方式传入
    参数1 character_vec_ 格式为 [("character_name",["","",""])]
    参数2 为包含所有类别的数组 格式为["class_X", "class_Y"]
    """
    self.class_set = {}
    # 记录该类别下各个特征值的条件概率
    character_condition_per = {}
    for character_name in character_vec_:
      character_condition_per[character_name[0]] = {}
      for character_value in character_name[1]:
        character_condition_per[character_name[0]][character_value] = {
          'num'      : 0, # 记录该类别下该特征值在训练样本中的数量,
          'condition_per' : 0.0 # 记录该类别下各个特征值的条件概率
        }
    for class_name in class_vec:
      self.class_set[class_name] = {
        'num'           : 0, # 记录该类别在训练样本中的数量,
        'class_per'        : 0.0, # 记录该类别在训练样本中的先验概率,
        'character_condition_per' : copy.deepcopy(character_condition_per),
      }
    #print("init", character_vec_, self.class_set) #for debug
  def learn(self, sample_):
    """
    learn 参数为训练的样本，格式为
    [
      {
        'character' : {'character_A':'A1'}, #特征向量
        'class_name' : 'class_X'       #类别名称
      }
    ]
    """
    for each_sample in sample:
      character_vec = each_sample['character']
      class_name   = each_sample['class_name']
      data_for_class = self.class_set[class_name]
      data_for_class['num'] += 1
      # 各个特质值数量加1
      for character_name in character_vec:
        character_value = character_vec[character_name]
        data_for_character = data_for_class['character_condition_per'][character_name][character_value]
        data_for_character['num'] += 1
    # 数量计算完毕， 计算最终的概率值
    sample_num = len(sample)
    for each_sample in sample:
      character_vec = each_sample['character']
      class_name  = each_sample['class_name']
      data_for_class = self.class_set[class_name]
      # 计算类别的先验概率
      data_for_class['class_per'] = float(data_for_class['num']) / sample_num
      # 各个特质值的条件概率
      for character_name in character_vec:
        character_value = character_vec[character_name]
        data_for_character = data_for_class['character_condition_per'][character_name][character_value]
        data_for_character['condition_per'] = float(data_for_character['num']) / data_for_class['num']
    from pprint import pprint
    pprint(self.class_set) #for debug
  def classify(self, input_):
    """
      对输入进行分类，输入input的格式为
    {
      "character_A":"A1",
      "character_B":"B3",
    }
    """
    best_class = ''
    max_per  = 0.0
    for class_name in self.class_set:
      class_data = self.class_set[class_name]
      per = class_data['class_per']
      # 计算各个特征值条件概率的乘积
      for character_name in input_:
        character_per_data = class_data['character_condition_per'][character_name]
        per = per * character_per_data[input_[character_name]]['condition_per']
      print(class_name, per)
      if per >= max_per:
        best_class = class_name
    return best_class
character_vec = [("character_A",["A1","A2","A3"]), ("character_B",["B1","B2","B3"])]
class_vec   = ["class_X", "class_Y"]
bayes = native_bayes_t(character_vec, class_vec)
sample = [
      {
        'character' : {'character_A':'A1', 'character_B':'B1'}, #特征向量
        'class_name' : 'class_X'       #类别名称
      },
      {
        'character' : {'character_A':'A3', 'character_B':'B1'}, #特征向量
        'class_name' : 'class_X'       #类别名称
      },
      {
        'character' : {'character_A':'A3', 'character_B':'B3'}, #特征向量
        'class_name' : 'class_X'       #类别名称
      },
      {
        'character' : {'character_A':'A2', 'character_B':'B2'}, #特征向量
        'class_name' : 'class_X'       #类别名称
      },
      {
        'character' : {'character_A':'A2', 'character_B':'B2'}, #特征向量
        'class_name' : 'class_Y'       #类别名称
      },
      {
        'character' : {'character_A':'A3', 'character_B':'B1'}, #特征向量
        'class_name' : 'class_Y'       #类别名称
      },
      {
        'character' : {'character_A':'A1', 'character_B':'B3'}, #特征向量
        'class_name' : 'class_Y'       #类别名称
      },
      {
        'character' : {'character_A':'A1', 'character_B':'B3'}, #特征向量
        'class_name' : 'class_Y'       #类别名称
      },
    ]
input_data ={
  "character_A":"A1",
  "character_B":"B3",
}
bayes.learn(sample)
print(bayes.classify(input_data))