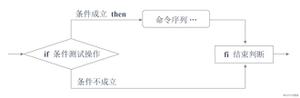
JS使用Prim算法和Kruskal算法实现最小生成树
之前都是看书,大部分也是c++的实现,但是搞前端不能忘了JS啊,所以JS实现一遍这两个经典的最小生成树算法。
一、权重图和最小生成树
权重图:图的边带权重
最小生成树:在连通图的所有生成树中,所有边的权重和最小的生成树
本文使用的图如下:
它的最小生成树如下:
二、邻接矩阵
邻接矩阵:用来表示图的矩阵就是邻接矩阵,其中下标表示顶点,矩阵中的值表示边的权重(或者有无边,方向等)。
本文在构建邻接矩阵时,默认Number.MAX_SAFE_INTEGER表示两个节点之间没有边,Number.MIN_SAFE_INTEGER表示当前节点没有自环。
代码如下:
/**
* 邻接矩阵
* 值为顶点与顶点之间边的权值,0表示无自环,一个大数表示无边(比如10000)
* */
const MAX_INTEGER = Number.MAX_SAFE_INTEGER;//没有的边
const MIN_INTEGER = Number.MIN_SAFE_INTEGER;//没有自环
const matrix= [
[MIN_INTEGER, 9, 2, MAX_INTEGER, 6],
[9, MIN_INTEGER, 3, MAX_INTEGER, MAX_INTEGER],
[2, 3, MIN_INTEGER, 5, MAX_INTEGER],
[MAX_INTEGER, MAX_INTEGER, 5, MIN_INTEGER, 1],
[6, MAX_INTEGER, MAX_INTEGER, 1, MIN_INTEGER]
];
这个邻接矩阵表示的图如下:
三、 边的表示
一个边具有权重、起点、重点三个属性,所以可以创建一个类(对象),实现如下:
/**
* 边对象
* */
function Edge(begin, end, weight) {
this.begin = begin;
this.end = end;
this.weight = weight;
}
Edge.prototype.getBegin = function () {
return this.begin;
};
Edge.prototype.getEnd = function () {
return this.end;
};
Edge.prototype.getWeight = function () {
return this.weight;
};
/*class Edge {
constructor(begin, end, weight) {
this.begin = begin;
this.end = end;
this.weight = weight;
}
getBegin() {
return this.begin;
}
getEnd() {
return this.end;
}
getWeight() {
return this.weight;
}
}*/
PS:JS这门语言没有私有变量的说法,这里写get方法纯粹是模拟一下私有变量。可以不用这么写,可以直接通过属性访问到属性值。
四、Prim算法
将这个算法的文章数不胜数,这里就不细说了。
其大体思路就是:以某顶点为起点,逐步找各顶点上最小权值的相邻边构建最小生成树,同时其邻接点纳入生成树的顶点中,只要保证顶点不重复添加即可。
实现代码如下:
/**
* Prim算法
* 以某顶点为起点,逐步找各顶点上最小权值的边构建最小生成树,同时其邻接点纳入生成树的顶点中,只要保证顶点不重复添加即可
* 使用邻接矩阵即可
* 优点:适合点少边多的情况
* @param matrix 邻接矩阵
* @return Array 最小生成树的边集数组
* */
function prim(matrix) {
const rows = matrix.length,
cols = rows,
result = [],
savedNode = [0];//已选择的节点
let minVex = -1,
minWeight = MAX_INTEGER;
for (let i = 0; i < rows; i++) {
let row = savedNode[i],
edgeArr = matrix[row];
for (let j = 0; j < cols; j++) {
if (edgeArr[j] < minWeight && edgeArr[j] !== MIN_INTEGER) {
minWeight = edgeArr[j];
minVex = j;
}
}
//保证所有已保存节点的相邻边都遍历到
if (savedNode.indexOf(minVex) === -1 && i === savedNode.length - 1) {
savedNode.push(minVex);
result.push(new Edge(row, minVex, minWeight));
//重新在已加入的节点集中找权值最小的边的外部边
i = -1;
minWeight = MAX_INTEGER;
//已加入的边,去掉,下次就不会选这条边了
matrix[row][minVex] = MAX_INTEGER;
matrix[minVex][row] = MAX_INTEGER;
}
}
return result;
}
五、Kruskal算法
介绍这个算法的文章也很多,这里不细说。
其主要的思路就是:遍历所有的边,按权值从小到大排序,每次选取当前权值最小的边,只要不构成回环,则加入生成树。
5.1 邻接矩阵转成边集数组
与Prim算法不同,Kruskal算法是从最小权值的边开始的,所以使用边集数组更方便。所以需要将邻接矩阵转成边集数组,并且按照边的权重从小到大排序。
/**
* 邻接矩阵转边集数组的函数
* @param matrix 邻接矩阵
* @return Array 边集数组
* */
function changeMatrixToEdgeArray(matrix) {
const rows = matrix.length,
cols = rows,
result = [];
for (let i = 0; i < rows; i++) {
const row = matrix[i];
for(let j = 0 ; j < cols; j++) {
if(row[j] !== MIN_INTEGER && row[j] !== MAX_INTEGER) {
result.push(new Edge(i, j, row[j]));
matrix[i][j] = MAX_INTEGER;
matrix[j][i] = MAX_INTEGER;
}
}
}
result.sort((a, b) => a.getWeight() - b.getWeight());
return result;
}
5.2 Kruskal算法的具体实现
Kruskal算法的一个要点就是避免环路,这里采用一个数组来保存已纳入生成树的顶点和边(连线),其下标是边(连线)的起点,下标对应的元素值是边(连线)的终点。下标对应的元素值为0,表示还没有以它为起点的边(连线)。
连线:表示一条或多条边前后连接形成的一条线,这条线没有环路。
/**
* kruskal算法
* 遍历所有的边,按权值从小到大排序,每次选取当前权值最小的边,只要不构成回环,则加入生成树
* 邻接矩阵转换成边集数组
* 优点:适合点多边少的情况
* @param matrix 邻接矩阵
* @return Array 最小生成树的边集数组
* */
function kruskal(matrix) {
const edgeArray = changeMatrixToEdgeArray(matrix),
result = [],
//使用一个数组保存当前顶点的边的终点,0表示还没有已它为起点的边加入
savedEdge = new Array(matrix.length).fill(0);
for (let i = 0, len = edgeArray.length; i < len; i++) {
const edge = edgeArray[i];
const n = findEnd(savedEdge, edge.getBegin());
const m = findEnd(savedEdge, edge.getEnd());
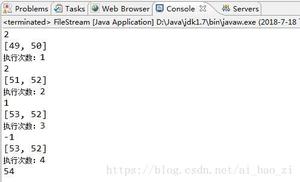
console.log(savedEdge, n, m);
//不相等表示这条边没有与现有生成树形成环路
if (n !== m) {
result.push(edge);
//将这条边的结尾顶点加入数组中,表示顶点已在生成树中
savedEdge[n] = m;
}
}
return result;
}
/**
* 查找连线顶点的尾部下标
* @param arr 判断边与边是否形成环路的数组
* @param start 连线开始的顶点
* @return Number 连线顶点的尾部下标
* */
function findEnd(arr, start) {
//就是一直循环,直到找到终点,如果没有连线,就返回0
while (arr[start] > 0) {
start = arr[start];
}
return start;
}
以上是 JS使用Prim算法和Kruskal算法实现最小生成树 的全部内容, 来源链接: utcz.com/z/328693.html