C++实现二叉树基本操作详解
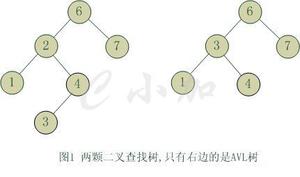
树是一种重要的非线性数据结构,二叉树是树型结构的一种重要类型。本学年论文介绍了二叉树的定义,二叉树的存储结构,二叉树的相关术语,以此引入二叉树这一概念,为展开二叉树的基本操作做好理论铺垫。二叉树的基本操作主要包含以下几个模块:二叉树的遍历方法,计算二叉树的结点个数,计算二叉树的叶子结点个数,二叉树深度的求解等内容。
前序遍历(递归&非递归)
- 访问根节点
- 前序访问左子树
- 前序访问右子树
//前序非递归
void PrevOrder()
{
stack<Node*> s;
Node *cur = _root;
while (cur || !s.empty())
{
while (cur)
{
cout << cur->_data << " ";
s.push(cur);
cur = cur->_left;
}
//此时当前节点的左子树已遍历完毕
Node *tmp = s.top();
s.pop();
cur = tmp->_right;
}
cout << endl;
}
//前序递归
void PrevOrderR()
{
_PrevOrder(_root);
cout << endl;
}
void _PrevOrder(Node *root)
{
if (root == NULL) //必须有递归出口!!!
return;
cout << root->_data << " ";
_PrevOrder(root->_left);
_PrevOrder(root->_right);
}
中序遍历(递归&非递归)
- 中序访问左子树
- 访问根节点
- 中序访问右子树
//中序非递归
void InOrder()
{
stack<Node*> s;
Node *cur = _root;
while (cur || !s.empty())
{
while (cur)
{
s.push(cur);
cur = cur->_left;
}
//此时当前节点的左子树已遍历完毕
Node *tmp = s.top();
cout << tmp->_data << " ";
s.pop();
cur = tmp->_right;
}
cout << endl;
}
//中序递归
void InOrderR()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node *root)
{
if (root == NULL)
return;
_InOrder(root->_left);
cout << root->_data << " ";
_InOrder(root->_right);
}
后序遍历(递归&非递归)
//后序非递归
//后序遍历可能会出现死循环,所以要记录下前一个访问的节点
void PostOrder()
{
stack<Node*> s;
Node *cur = _root;
Node *prev = NULL;
while (cur || !s.empty())
{
while (cur)
{
s.push(cur);
cur = cur->_left;
}
Node *tmp = s.top();
if (tmp->_right && tmp->_right != prev)
{
cur = tmp->_right;
}
else
{
cout << tmp->_data << " ";
prev = tmp;
s.pop();
}
}
cout << endl;
}
//后序递归
void PostOrderR()
{
_PostOrder(_root);
cout << endl;
}
void _PostOrder(Node *root)
{
if (root == NULL)
return;
_PostOrder(root->_left);
_PostOrder(root->_right);
cout << root->_data << " ";
}
层序遍历
从根节点开始,依次访问每层结点。
利用队列先进先出的特性,把每层结点从左至右依次放入队列。
void LevelOrder() //利用队列!!!
{
queue<Node*> q;
Node *front = NULL;
//1.push根节点
if (_root)
{
q.push(_root);
}
//2.遍历当前节点,push当前节点的左右孩子,pop当前节点
//3.遍历当前节点的左孩子,再遍历右孩子,循环直至队列为空
while (!q.empty())
{
front = q.front();
cout << front->_data << " ";
if (front->_left)
q.push(front->_left);
if (front->_right)
q.push(front->_right);
q.pop();
}
cout << endl;
}
求二叉树的高度
size_t Depth()
{
return _Depth(_root);
}
size_t _Depth(Node *root)
{
if (root == NULL)
return 0;
else if (root->_left == NULL && root->_right == NULL)
return 1;
else
{
size_t leftDepth = _Depth(root->_left) + 1;
size_t rightDepth = _Depth(root->_right) + 1;
return leftDepth > rightDepth ? leftDepth : rightDepth;
}
}
求叶子节点的个数
size_t LeafSize()
{
return _LeafSize(_root);
}
size_t _LeafSize(Node *root)
{
if (root == NULL)
return 0;
else if (root->_left == NULL && root->_right == NULL)
return 1;
else
return _LeafSize(root->_left) + _LeafSize(root->_right);
}
求二叉树第k层的节点个数
size_t GetKLevel(int k)
{
return _GetKLevel(_root, k);
}
size_t _GetKLevel(Node *root, int k)
{
if (root == NULL)
return 0;
else if (k == 1)
return 1;
else
return _GetKLevel(root->_left, k - 1) + _GetKLevel(root->_right, k - 1);
}
完整代码如下:
template<class T>
struct BinaryTreeNode
{
T _data;
BinaryTreeNode *_left;
BinaryTreeNode *_right;
BinaryTreeNode(const T& d)
:_data(d)
, _left(NULL)
, _right(NULL)
{}
};
template<class T>
class BinaryTree
{
public:
typedef BinaryTreeNode<T> Node;
BinaryTree()
:_root(NULL)
{}
BinaryTree(T *arr, size_t n, const T& invalid)
{
size_t index = 0;
_root = _CreateBinaryTree(arr, n, invalid, index);
}
BinaryTree(const BinaryTree<T>& t)
:_root(NULL)
{
_root = _CopyTree(t._root);
}
BinaryTree<T>& operator=(const BinaryTree<T>& t)
{
if (this != t)
{
Node *tmp = new Node(t._root);
if (tmp != NULL)
{
delete _root;
_root = tmp;
}
}
return *this;
}
~BinaryTree()
{
_DestroyTree(_root);
cout << endl;
}
//前序非递归
void PrevOrder()
{
stack<Node*> s;
Node *cur = _root;
while (cur || !s.empty())
{
while (cur)
{
cout << cur->_data << " ";
s.push(cur);
cur = cur->_left;
}
//此时当前节点的左子树已遍历完毕
Node *tmp = s.top();
s.pop();
cur = tmp->_right;
}
cout << endl;
}
//前序递归
void PrevOrderR()
{
_PrevOrder(_root);
cout << endl;
}
//中序非递归
void InOrder()
{
stack<Node*> s;
Node *cur = _root;
while (cur || !s.empty())
{
while (cur)
{
s.push(cur);
cur = cur->_left;
}
//此时当前节点的左子树已遍历完毕
Node *tmp = s.top();
cout << tmp->_data << " ";
s.pop();
cur = tmp->_right;
}
cout << endl;
}
//中序递归
void InOrderR()
{
_InOrder(_root);
cout << endl;
}
//后序非递归
//后序遍历可能会出现死循环,所以要记录下前一个访问的节点
void PostOrder()
{
stack<Node*> s;
Node *cur = _root;
Node *prev = NULL;
while (cur || !s.empty())
{
while (cur)
{
s.push(cur);
cur = cur->_left;
}
Node *tmp = s.top();
if (tmp->_right && tmp->_right != prev)
{
cur = tmp->_right;
}
else
{
cout << tmp->_data << " ";
prev = tmp;
s.pop();
}
}
cout << endl;
}
//后序递归
void PostOrderR()
{
_PostOrder(_root);
cout << endl;
}
void LevelOrder() //利用队列!!!
{
queue<Node*> q;
Node *front = NULL;
//1.push根节点
if (_root)
{
q.push(_root);
}
//2.遍历当前节点,push当前节点的左右孩子,pop当前节点
//3.遍历当前节点的左孩子,再遍历右孩子,循环直至队列为空
while (!q.empty())
{
front = q.front();
cout << front->_data << " ";
if (front->_left)
q.push(front->_left);
if (front->_right)
q.push(front->_right);
q.pop();
}
cout << endl;
}
size_t Size()
{
return _Size(_root);
}
size_t LeafSize()
{
return _LeafSize(_root);
}
size_t GetKLevel(int k)
{
return _GetKLevel(_root, k);
}
size_t Depth()
{
return _Depth(_root);
}
Node* Find(const T& d)
{
return _Find(_root, d);
}
protected:
Node* _CreateBinaryTree(T *arr, size_t n, const T& invalid, size_t& index)
{
Node *root = NULL;
if (index < n && arr[index] != invalid)
{
root = new Node(arr[index]);
index++;
root->_left = _CreateBinaryTree(arr, n, invalid, index);
index++;
root->_right = _CreateBinaryTree(arr, n, invalid, index);
}
return root;
}
Node* _CopyTree(Node *root)
{
Node *newRoot = NULL;
if (root)
{
newRoot = new Node(root->_data);
newRoot->_left = _CopyTree(root->_left);
newRoot->_right = _CopyTree(root->_right);
}
return newRoot;
}
void _DestroyTree(Node *root)
{
if (root)
{
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
}
void _PrevOrder(Node *root)
{
if (root == NULL) //必须有递归出口!!!
return;
cout << root->_data << " ";
_PrevOrder(root->_left);
_PrevOrder(root->_right);
}
void _InOrder(Node *root)
{
if (root == NULL)
return;
_InOrder(root->_left);
cout << root->_data << " ";
_InOrder(root->_right);
}
void _PostOrder(Node *root)
{
if (root == NULL)
return;
_PostOrder(root->_left);
_PostOrder(root->_right);
cout << root->_data << " ";
}
size_t _Size(Node *root)
{
if (root == NULL)
return 0;
else
return _Size(root->_left) + _Size(root->_right) + 1;
}
size_t _LeafSize(Node *root)
{
if (root == NULL)
return 0;
else if (root->_left == NULL && root->_right == NULL)
return 1;
else
return _LeafSize(root->_left) + _LeafSize(root->_right);
}
size_t _GetKLevel(Node *root, int k)
{
if (root == NULL)
return 0;
else if (k == 1)
return 1;
else
return _GetKLevel(root->_left, k - 1) + _GetKLevel(root->_right, k - 1);
}
size_t _Depth(Node *root)
{
if (root == NULL)
return 0;
else if (root->_left == NULL && root->_right == NULL)
return 1;
else
{
size_t leftDepth = _Depth(root->_left) + 1;
size_t rightDepth = _Depth(root->_right) + 1;
return leftDepth > rightDepth ? leftDepth : rightDepth;
}
}
Node* _Find(Node *root, const T& d)
{
if (root == NULL)
return NULL;
else if (root->_data == d)
return root;
else if (Node *ret = _Find(root->_left, d))
return ret;
else
_Find(root->_right, d);
}
protected:
Node *_root;
};
以上是 C++实现二叉树基本操作详解 的全部内容, 来源链接: utcz.com/z/319417.html