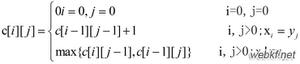最长递增子序列

• Z时代
• 2024-01-10
• 分类：综合

最长增加子序列是一个项目大于前一个项目的子序列。在这里，我们将尝试从一组整数中找到最长增加子序列的长度。

输入输出

Input:
A set of integers. {0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}
Output:
The length of longest increasing subsequence. Here it is 6.
The subsequence is 0, 2, 6, 9, 13, 15.

算法

longestSubSeq(subarray, n)

输入-子数组和子数组的大小。

输出-最长增加的子序列长度。

Begin
   define array length of size n
   initially set 0 to all entries of length
   for i := 1 to n-1, do
      for j := 0 to i-1, do
         if subarray[j] < subarray[i] and length[j] > length[i], then length[i] := length[j]
      done
      increase length[i] by 1
   done
   lis := 0
   for i := 0 to n-1, do
      lis := maximum of lis and length[i]
   done
   return lis
End

示例

#include <iostream>
using namespace std;
int longestSubSeq(int subArr[], int n) {
   int length[n] = { 0 };                    //set all length to 0
   length[0] = 1;                            //subsequence ending with subArr[0] is 1
   for (int i = 1; i < n; i++) {            //ignore first character, second to all
      for (int j = 0; j < i; j++) {         //subsequence ends with subArr[j]
         if (subArr[j] < subArr[i] && length[j] > length[i])
            length[i] = length[j];
      }
      length[i]++;              //add arr[i]
   }
   int lis = 0;
   for (int i = 0; i<n; i++)           // find longest increasing subsequence
      lis = max(lis, length[i]);
   return lis;
}
int main() {
   int arr[] = { 0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15};
   int n = 16
   cout << "最长递增子序列的长度是： " << longestSubSeq(arr, n);
   return 0;
}

输出结果

最长递增子序列的长度是： 6

以上是 最长递增子序列 的全部内容， 来源链接： utcz.com/z/317040.html