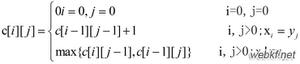除C ++中的最小和最大元素外,所有大小为K的子序列的乘积
给定数组arr [n],其中包含n个整数和一个用于定义大小的整数k;任务是打印大小为k的所有子序列的乘积,最小和最大元素除外。
假设我们有一组4个元素{1、2、3、4}和k为2,那么它的子集将是-{1,2},{2、3},{3、4},{1, 4},{1、3},{2、4}
因此,排除最大元素4和最小元素1,其余元素将为-
2,3,3,3,2,其乘积将为-
2 * 3 * 3 * 3 * 2 = 108
同样,我们必须解决问题
示例
Input: arr[] = {3, 4, 1, 7}, k = 3Output: 144
Explanation: subset will be, {3, 4, 1}, {4, 1, 7}, {3, 1, 7}, {3, 4, 7}
Eliminating maximum value 7 and minimum 1 we will get:
{3, 4}, {4}, {3}, {3, 4}, so multiplying these will give us:
3 * 4 * 4 * 3 = 144
Input: arr[] = {1, 2, 3, 4}, k = 3
Output: 36
我们用来解决上述问题的方法-
可以有很多方法来实现该解决方案。有一种方法可以一一生成所有可能的子序列,然后乘积除集合的最大值和最小值之外的所有元素。尽管这种方法很容易实现,但是具有很高的复杂度,并且效率低下。
我们也有一种有效的方法,在这种方法中,我们将首先对数组进行排序,而不考虑要考虑的子集或后续子集。
然后,我们将逐个计算每个元素的出现次数。
可以出现一个C(k-1)(n-1)个子序列,其中C(k-1)(i)次我们将出现的最大元素C(k-1)(ni-1)次作为该子序列的最小元素。
因此,我们可以说这是一种更有效的方法,因为第i个元素将会发生-
C(k-1)(n-1)-C(k-1)(i)-C(k-1)(ni-1)次。
现在,首先我们将为arr [i]中的每个元素求解x,因此它的答案可能真的很难计算,因此可以使用费马小定理。
注意-由于答案可能非常大,因此我们将以109 + 7的mod打印答案。
算法
StartStep 1-> Declare function to calculate the pairs combination
void pairs(int a, int b)
Declare int i, j
Loop For i = 0 and i <= a and i++
Loop For j = 0 and j <= min(i, b) and j++
IF (j == 0 || j == i)
Set c[i][j] = 1
End
Else
Set c[i][j] = (c[i - 1][j - 1] % val + c[i - 1][j] % val) % val
End
End
End
Step 2-> declare function for power
LL power(LL x, unsigned LL y)
Declare unsigned LL temp = 1
Set x = x % val
Loop While (y > 0)
IF(y & 1)
Set temp = (temp * x) % val
End
Set y = y >> 1
Set x = (x * x) % val
End
return temp % val
Step 3-> Declare 函数计算所有子序列的乘积
unsigned LL product(LL arr[], int size, int k)
Declare and set unsigned LL temp = 1
Call function to sort an array as sort(arr, arr + size)
Declare and set as LL pow = c[size - 1][k - 1]
Loop For i = 0 and i < size and i++
Declare and set LL pow_l = c[i][k - 1]
Declare and set LL pow_f = c[size - i - 1][k - 1]
Declare and set LL pow_e = ((pow % val) - (pow_l + pow_f) % val + val) % val
Declare and set unsigned LL mul = power(arr[i], pow_e) % val
Set temp = ((temp % val) * (mul % val)) % val
End
return temp % val
Step 4-> In main() Call pairs(100, 100)
Declare and set LL arr[] = { 3, 4, 1, 7 }
Calculate size as int size = sizeof(arr) / sizeof arr[0]
Declare and set int k = 3
Declare and set unsigned LL temp = product(arr, size, k)
Print temp
Stop
示例
#include <bits/stdc++.h>using namespace std;
#define val 1000000007
#define LL long long
#define max 101
LL c[max - 1][max - 1];
LL power(LL x, unsigned LL y) {
unsigned LL temp = 1;
x = x % val;
while (y > 0) {
if (y & 1) {
temp = (temp * x) % val;
}
y = y >> 1;
x = (x * x) % val;
}
return temp % val;
}
void pairs(int a, int b) {
int i, j;
for (i = 0; i <= a; i++) {
for (j = 0; j <= min(i, b); j++) {
if (j == 0 || j == i)
c[i][j] = 1;
else
c[i][j] = (c[i - 1][j - 1] % val + c[i - 1][j] % val) % val;
}
}
}
//函数计算所有子序列的乘积
unsigned LL product(LL arr[], int size, int k) {
unsigned LL temp = 1;
//排序数组
sort(arr, arr + size);
LL pow = c[size - 1][k - 1];
for (int i = 0; i < size; i++) {
LL pow_l = c[i][k - 1];
LL pow_f = c[size - i - 1][k - 1];
LL pow_e = ((pow % val) - (pow_l + pow_f) % val + val) % val;
unsigned LL mul = power(arr[i], pow_e) % val;
temp = ((temp % val) * (mul % val)) % val;
}
return temp % val;
}
int main() {
//所有对的总和
pairs(100, 100);
LL arr[] = { 3, 4, 1, 7 };
int size = sizeof(arr) / sizeof arr[0];
int k = 3;
unsigned LL temp = product(arr, size, k);
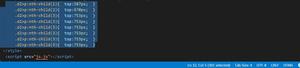
cout<<"除最小和最大元素外,所有大小为k的子序列的乘积为:"<<temp << endl;
return 0;
}
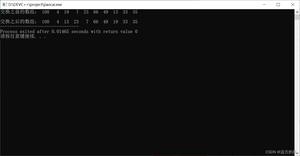
输出结果
除最小和最大元素外,所有大小为k的子序列的乘积为:144
以上是 除C ++中的最小和最大元素外,所有大小为K的子序列的乘积 的全部内容, 来源链接: utcz.com/z/316455.html