Dynamic Routing Between Capsules 译文
摘要
胶囊(capsule)是一组神经元,神经元中的向量用以表示特定类型实体(例如对象或对象部分)的参数。我们使用向量的长度来表示实体存在的可能性,用向量的方向来表示实体的方向①。
在一个层次上的被激活的胶囊,通过变换矩阵对更高层次的胶囊的实例化参数进行预测。 当多个预测一致时,更高层次的胶囊变得活跃。
我们表明,一个有识别训练的多层胶囊系统在MNIST上实现了最先进的性能,并且在识别高度重叠的数字方面比卷积网络好得多②。
为了达到这些结果,我们使用了一种迭代路由协议机制:使得一个低层次的胶囊,更倾向于将它的结果输出到能产生更大标量结果的,更高层次的胶囊中。
译者注:①为便于理解我们所说的实体、实例,以及向量如何表达实体的参数,有必要进行一些附加的解释:
简而言之,一个胶囊网络是由胶囊而不是由神经元构成。一个胶囊是一小群神经元,它们可以学习在一个图片的一定区域内检查一个特定的对象(比如,一个矩形)。
它的输出是一个向量(例如,一个 8 维的向量)。每个向量的长度代表了物体是否存在的估计概率 [1],它的方向(例如在8维空间里)记录了物体的姿态参数(比如,精确的位置、旋转等)。如果物体有稍微的变化(比如,移动、旋转、尺寸变化等),胶囊将也会输出一个长度相同但是方向稍微变化的向量。因此胶囊是等变的。
和常规神经网络很类似,CapsNet 也是由多层构成(见下图)。处于最底层的胶囊被称为向量胶囊:它们每个都只用图片的一小部分区域作为输入(称为感知域),然后试图去探测某个特殊的模式(例如,一个矩形)是否存在,以及姿态如何。在更高层的胶囊(称为路由胶囊)则是探测更大和更复杂的物体,比如船等。
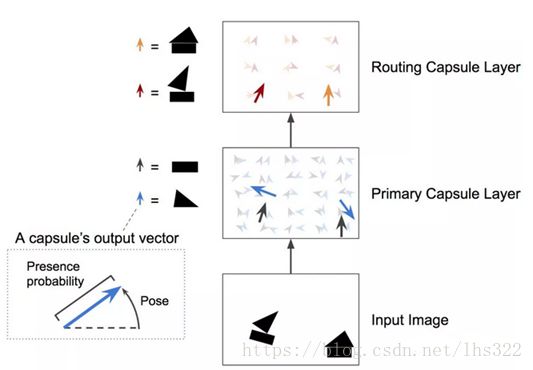

②高度重叠的数字指的是multiMIST数据集
1 简介
人类视觉通过聚焦于确定的固定点,并忽略其他不相关的细节,以确保只对极小部分的光学影像以最高分辨率进行处理。在本文中,我们将假设单个注视点给我们提供的信息不仅仅是简单的识别的对象,或获得其属性。我们假设我们的多层视觉系统在每个注视点上创建了一个类似于树状结构的解析结构,并且我们忽略了这些单注视点解析树如何在多个注视点上进行协调的问题。
分析树通常通过动态分配内存来动态构建。
继Hinton等人的研究[2000]我们假设,对于单一的固定点,胶囊是在网络中通过训练所生成的③。
每层将被分成许多小组称为“胶囊”的神经元(Hinton et al。[2011]),并且分析树中的每个节点将对应一个活动胶囊。
使用迭代路由过程,每个活动胶囊将在上面的图层中选择一个胶囊作为其树中的父代。
对于视觉系统的高层次来说,这个迭代过程将解决将部分分配给整体的问题。
注③:此句为译者所译,原文为:a parse tree is carved out of a fixed multilayer neural network like a sculpture is carved from a rock.
活动胶囊内神经元的活动表示图像中存在的特定实体的各种属性。
这些属性可以包括许多不同类型的实例化参数,例如姿势(位置,大小,方向),变形,速度,反射率,色调,纹理等。一个非常特殊的属性是图像中实例化实体的存在。
表示存在的一个显而易见的方法是使用一个单独的逻辑单元,其输出是实体存在的概率。在本文中,我们探索了一个有趣的替代方法,即使用实例化参数向量的全部长度来表示实体的存在(概率),并规定向量的方向来表示实体的属性。
我们通过应用一个非线性(激活函数)保证矢量输出的长度不超过1,这个非线性使得矢量的方向保持不变,但是其量级减小(只控制在0-1之间)。
由于胶囊的输出是矢量,因此可以使用强大的动态路由机制来确保胶囊的输出被发送到上述层中的适当父代。最初,输出被路由到所有可能的父母结点,但是通过可以控制上下层次之间每对父子结点的系数的总和为1,可以达到动态路由的目的。对于每个可能的父亲,胶囊通过将其自身的输出乘以权重矩阵来计算“预测向量”。如果某个合适的父节点得到一个大的标量输出,那么就会有自上而下的反馈,这会增加该父亲的耦合系数,并减小其余父母结点的系数。这增加了胶囊对该父母的贡献,从而进一步增加了胶囊与父母输出的预测的标量乘积。这种类型的“通过协议路由”应该比由max-pooling实现的非常原始的路由形式更有效,这保证了一层中的神经元关注于下层中的最活跃的特征,同时忽略其他非活跃特征。我们证明我们的动态路由机制是实现分割高度重叠对象的“可解释”的有效方式。
卷积神经网络(CNN)学习特征检测器(滤波器)的提取的特征。这使得神经网络可以通过检测图片中的各种位置的特征,去训练自身的权重值。这已被证明对图像解释非常有帮助。但是,我们还是进行了CNN的改动,使用向量形式的输出替代了CNN中的标量输出;使用rooting-by-agreement代替了下采样maxpooling操作。但我们仍然希望像神经网络一样,可以跨空间提取和复制已知的特征。
为了达到这个目的,我们除了最后一层胶囊之外都是卷积式的。与CNN一样,我们使高层级的胶囊去处理图像的较大区域。然而,与最大池化不同,我们不会丢弃有关区域内实体的准确位置的信息。对于低层级的胶囊,位置信息是胶囊处于活动状态的“地点编码”。随着层级的提升,越来越多的低层级位置信息在胶囊的输出向量中以实值被计算为“速率编码”。从地点编码到速率编码的这种转变,再加上更高级别的胶囊代表了更多自由度更高的实体,这表明胶囊的维数应随着我们升级而增加。
2 如何计算胶囊的矢量输入和输出
有很多可能的方法可以实现胶囊的总体思想。本文的目的不是探索所有的实现方法,而仅仅是为了表明一个相当简单的实现就能够很好地工作,并且动态路由有所帮助。
我们希望胶囊的输出向量的长度表示胶囊代表的实体出现在当前输入中的概率。
因此,我们使用非线性的“squashing”激活函数来确保短矢量缩小到几乎为零,而长矢量缩小到略低于1的长度。
我们将其留待Discriminative Learning去使用,以充分利用这种非线性。

其中v j是胶囊j的矢量输出,s j是其总输入。
对于除第一层胶囊以外的所有胶囊,胶囊sj的总输入量是所有下一层及的“预测向量”的加权总和,并且通过将胶囊的输出ui乘以权重矩阵W ij③
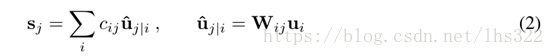
注③:可以通过下图辅助理解,本图摘自廖华东:
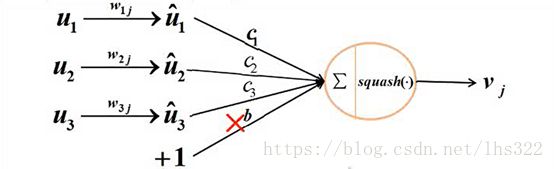
其中C ij是由迭代动态路由过程确定的耦合系数。 胶囊i与上述层中所有胶囊之间的耦合系数总和为1,并且由“softmax”确定,其初始的logits b ij是胶囊i应该耦合至胶囊j的对数先验概率。

先验对数概率可以和其他权重同时被区别地学习。它们取决于两个胶囊的位置和类型,但不取决于当前输入图像。通过衡量当前胶囊j的输出vj与高一层级的胶囊i的预测û j|i的一致性,可以迭代地改进初始耦合系数。
该一致性只是标量积 a ij = v j .û j|i。在计算所有耦合系数的新值之前,将一致性看作是对数似然性并添加到初始logits和bij。
在卷积胶囊层中,每个胶囊使用网格的每个成员的不同变换矩阵以及每种胶囊的类型向上述层中的每种胶囊输出局部的向量网格。

3 损失函数
我们使用实例化向量的长度来表示胶囊实体存在的概率。 我们希望类k的顶层胶囊只有在图像中存在该数字时才具有长实例化矢量。 为了允许多个数字,我们使用单独的margin loss,对于每个数字胶囊k,使用Lk表示其损失:
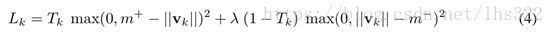
其中如果存在k类,那么T k = 1,且m + = 0.9且m -= 0.1。 对于缺少数字类别的损失,λ的下调权重会阻止初始学习缩小所有数字胶囊的活动向量的长度。 我们使用λ= 0.5。 总损失仅仅是所有数字胶囊损失的总和。
4 CapsNet 的架构
一个简单的CapsNet架构如图1所示。该架构很浅,只有两个卷积层和一个完全连接层。Conv 1拥有256个9×9卷积核,步长为1,ReLU激活。该图层将像素转换为局部特征的激活图,然后将其用作主胶囊(primary capsule)的输入。
主胶囊是多维实体的最低级别,并且从反向图形角度来看,激活主胶囊对应于反转渲染过程。比起将实例化的部分拼凑在一起来形成熟悉的整体(CNN就是这样的),这是一种非常不同的计算方法,这是胶囊设计的优点。
第二层(PrimaryCapsules)是具有32个卷积8D胶囊通道的卷积胶囊层(即,每个主胶囊包含8个卷积单元,9×9内核和步长为2)。 每个主胶囊单元的值,是通过计算Conv 1中所有256×81单位的输出,其感受野与胶囊中心的位置重叠。
PrimaryCapsules 有[32×6×6]胶囊输出(每个输出是一个8 D矢量),[6×6]网格中的每个胶囊彼此共享它们的权重。
人们可以将PrimaryCapsules看作具有公式1的卷积层。作为其块的非线性激活函数。 最后一层(DigitCaps)每个类有一个 16D 胶囊用来进行表示,每个胶囊都接收来自上层级中中所有胶囊的输出作为输入。
我们只在两个连续胶囊层之间进行路由(例如PrimaryCapsules和DigitCaps)。 由于Conv1的输出是1D,因此在其空间中没有方向可以达成一致。 因此,Conv 1和PrimaryCapsules之间不使用路由。
所有路由逻辑(bij)都被初始化为零。 因此,最初以相等的概率(c ij)将胶囊输出(u i)发送到所有父胶囊(v 0 … v 9)。
我们的实现在TensorFlow中(Abadi et al。[2016]),我们使用Adam优化器(Kingma和Ba[2014])以及其TensorFlow默认参数(包括指数衰减学习率)来最小化式4中的边际损失的总和(margin loss)。
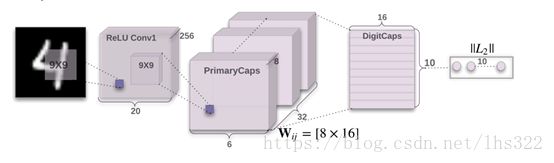
图1:一个简单的 3 层 CapsNet。 该模型给深度卷积网络(如 Chang 和 Chen [2015])提供了可比较的结果。
DigitCaps 层中每个胶囊的活动向量的长度表示存在每个类的实例并用于计算分类损失。 W ij 是 Primary Capsules 中的每个 ui,i∈(1,32×6×6)与v j,j∈(1,10)之间的权重矩阵。
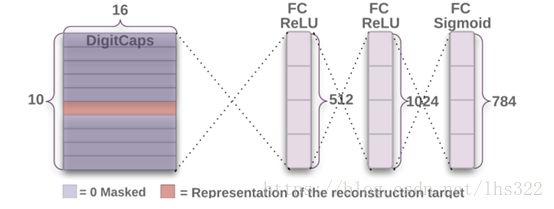
图2:解码器结构,用于重建 DigitCaps 图层表示中的数字。 在训练期间,图像与 sigmoid 层的输出之间的欧几里得距离被最小化。我们在训练中使用真实的标签作为预测重建目标。
以上是 Dynamic Routing Between Capsules 译文 的全部内容, 来源链接: utcz.com/z/264682.html