Python Binary Search Tree 二叉搜索树
二叉搜索树,也叫二叉查找树(Binary Search Tree,BST),特性是每个结点的值都比左子树大,比右子树小。中序遍历是递增的
实现
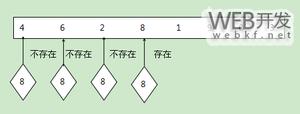
find_item(item, root) —— 寻找树中等于某个值的结点,利用 BST 的特性,若一个结点比该值大,则往结点的左边寻找,若一个结点比该值小,则往结点的右边寻找。时间复杂度为 O(log n)
def find_item(item, root):if not root:
return None
while root:
if root.val == item:
return root
elif root.val > item:
root = root.left
else:
root = root.right
return None
find_max(root) —— 寻找树中值最大的结点。由于是 BST,最大的结点一定在树的最右边
def find_max(root):if not root:
return None
while root.right:
root = root.right
return root
find_min(root) —— 寻找值最小的结点,一定在树的最左边
def find_min(root):if not root:
return None
while root.left:
root = root.left
return root
add_node(value, root) —— 在二叉搜索树中插入一个新的元素,若元素已存在则忽略
def add_node(value, root):if not root:
return treeNode(value)
if value > root.val:
root.right = add_node(value, root.right) # 递归插入右子树
elif value < root.val:
root.left = add_node(value, root.left) # 递归插入左子树
else:
pass # 如果value已经存在,则什么也不做
return root
delete_node(value, root) —— 删除一个结点,分三种情况:
- 要删除的是叶结点:直接删除,将父结点的指针指向 None
- 要删除的结点只有一个子结点:直接将父结点的指针指向这个子结点
- 要删除的结点有左、右两个结点(最复杂的情况):选取另一结点代替被删结点——右子树的最小元素或左子树的最大元素。可以看到,右子树的最小元素或左子树的最大元素都是最多只有一个子结点,因此对它们的删除操作也很简单
def delete_node(value, root):if not root:
return None # 说明要删除的元素未找到
if value < root.val:
root.left = delete_node(value, root.left) # 左子树递归删除
elif value > root.val:
root.right = delete_node(value, root.right) # 右子树递归删除
else: # 说明已经找到要删除的结点了
if not root.left: # 只有右子树或者没有子结点
return root.right
elif not root.right: # 只有左子树
return root.left
else: # 有左右两个结点
temp = find_min(root.right) # 在右子树中找到最小的元素
root.val = temp.val
root.right = delete_node(temp.val, root.right)
return root
以上是 Python Binary Search Tree 二叉搜索树 的全部内容, 来源链接: utcz.com/z/264534.html