为何会造成3+4等于5的困惑?3+4等于5难倒众多数学家?
为何说3+4等于5?小学生都会算的题目,究竟是怎么难倒众多数学家的?
问3+4在什么情况下等于5,这个问题好像赵本山小品中搞笑的脑筋急转弯一样,因为就连小学生都知道3+4等于7,而且毫无疑问是脱口而出。但是如果我告诉你3+4可能会等于7,你是不是觉得我的脑子坏了。

但这却是困扰数学家的一个问题,许多数学家挠破头都难以解释清楚的问题,而且这与我们日常所见的楼梯有关,所有又被称为楼梯悖论。我们每天都可能走上走下的楼梯,竟然暗藏数学悖论,实在让人觉得不可思议。
从单纯的算术上我们的确看不出任何3+4会等于7的可能性,但是如果把问题放在几何图形当中,就展现出了不一样的情况。为了方便理解,我们先在图上画一个最基础的二阶楼梯横截面,设定这个楼梯横截面的水平宽度为4,垂直的高度是3的话,那么整个楼梯的长度是多少呢?
通过分割的方法我们可以将这个二阶楼梯横截面中,两个楼梯台阶的横向线段看成是整个水平宽度的各二分之一,两个楼梯台阶的纵向线段,也可以看成是垂直高度的各二分之一。这样的话,这个二阶楼梯的长度就刚好等于水平宽度的4,加上竖直高度的3,楼梯的长度也就为7。而且不光是二阶,我们画一个4阶的楼梯横截面也是同样道理,只是将水平方向的距离和竖直方向的高度各看成四等份,楼梯的长度相加依然满足3+4等于7。
而且即使再增加更多的台阶数,通过分割的方法楼梯的长度都满足3+4,所以到这里一切都很正常,但是如果楼梯水平宽度和高度都保持不变,但是楼梯的台阶数无限增多的话,楼梯的长度就接近于直线,3+4等于5的困惑也就随之而来。
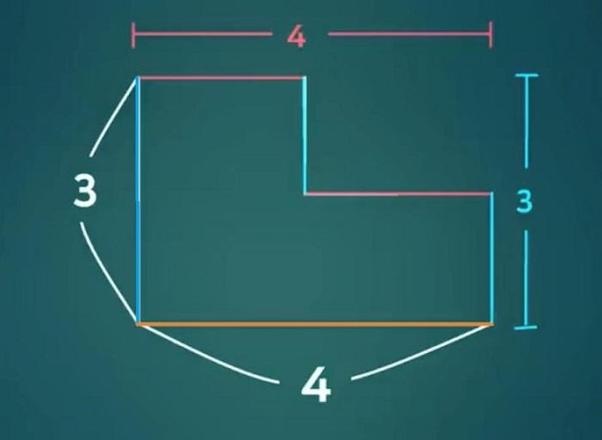
3+4等于5是如何算出来的,楼梯悖论中无限增多的台阶数,为何会造成3+4等于5的困惑?
当我们预先设置的楼梯水平宽度和垂直高度一直保持的是4和3,那么随着台阶数的增加,根据分割法算出的楼梯长度也一直是3+4之和。但是如果楼梯台阶数接近无限的状况下,便形成了一条直线,楼梯的横截面也从不规则的多边形变成了直角三角形。
那么三角形就可以符合勾股定理,无论是通过斜边长度的平方,等于两个直角边的平方之和来开根号计算,还是通过直接背诵勾三股四弦五的特定勾股数,都能得出这个直角三角形的斜边长是5。
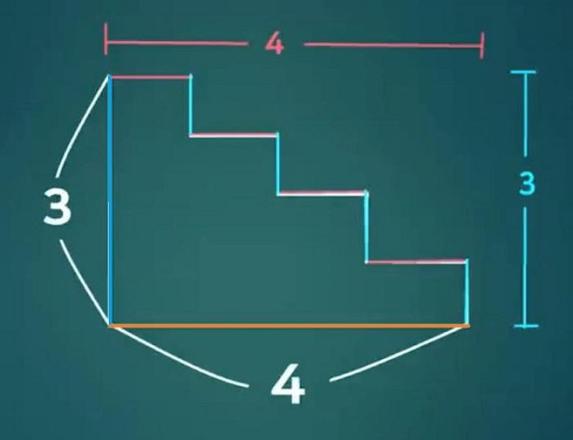
那么问题也就随之而来,利用分割法推理得出的楼梯长度应该是3+4,而3+4根据最基本的数学公理就是等于7,但是根据勾股定理算出的楼梯长度却是5,并且勾股定理从古至今也被全世界各国用了400多种方法证明过,是最基本的数学定理。
而楼梯的长度就在那里,无论用什么方法算都是同一个楼梯,为何会出现3+4等于5这样奇怪的现象呢?而且这根本不是因为精确度的问题造成的误差现象,也一度让数学家感到难以解释。
难道我们的数学世界就因为这个问题而要崩塌了吗?虽然这个问题并不会直接影响我们的实际生活,毕竟现实生活中不会需要建设一条无限个台阶的楼梯。我们日常上下楼梯时 ,也不会因为这个悖论而受到什么影响。
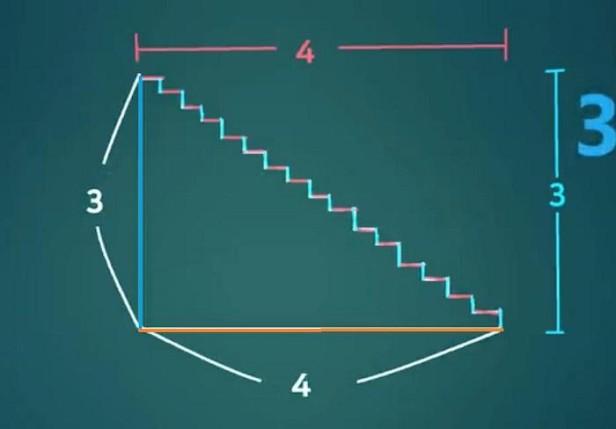
但是这样的悖论问题直接影响整个人类的逻辑思维,和辛苦建立起来的现代数学体系。未来人类势必会走向太空和宇宙,所要面临的空间尺度不是现在日常生活能够想象的,如果不能很好地解决这样的问题,就表明现代数学体系有可能会存在问题,那么未来有如何在这样的体系上发展更高的科技呢?不过好在最终这个问题被发现是个陷阱,能不能理解就要看你的空间想象能力了。
3+4等于5的奇怪楼梯悖论,是如何创造出来的秘密终于被揭开,那悖论的陷阱究竟设在哪里?
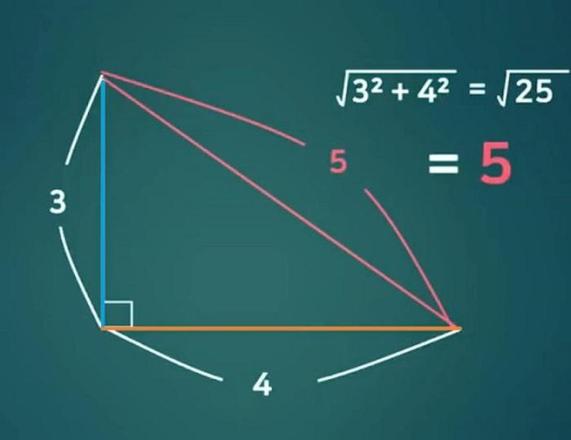
当一个水平宽度和垂直高度固定为4和3的楼梯,台阶数接近于无限时,通过分割法算出的楼梯长度是3+4应该等于7,而把楼梯长度看做是一个三角形的斜边算出来的长度便是5,但是这个楼梯悖论的问题,就恰恰出在这个“看做是”三个字之上。
因为其实这两个方法所算出的长度并不是一个长度,为了更好地理解我们将计算模型再倒回二阶楼梯横截面,如果从楼梯左侧最高点向右下方最低点连一条直线,那么这条直线的长度用勾股定理算出来的应该是5,也就是那个让我们非常费解的5。
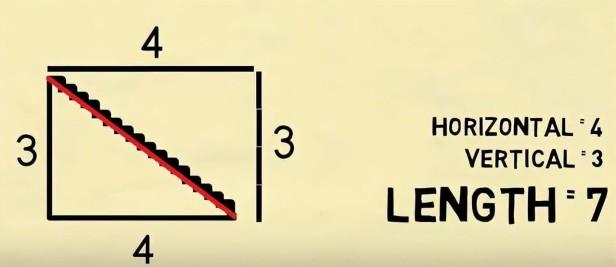
这时楼梯展现出来的长度根据分割法计算出来的应该是3+4等于7,并且这时不会有人认为这个连线长度的5,和楼梯长度的7有什么关系,因为他们看起来完全不同。而这个长度为5的斜边,我们不将其擦除的话,随着楼梯台阶数的不断增多,楼梯的长度在肉眼上也会无限接近于这个两点之间的连线。
但是如果能够放大的话,就会发现当楼梯长度表面上无限接近三角形斜边长度,但是内部仍然是由横向和纵向的无数个细小分割线段组成。就像一根较长的毛线,经过不断的细小弯折,放在一段较短的线段长度内,实际拉直的话长度会更长。所以实际上楼梯的长度,一直就是7,两点之间斜线的距离也一直是5都没有变化,变化的是楼梯的形状通过微小的弯折蜷缩在了一起。
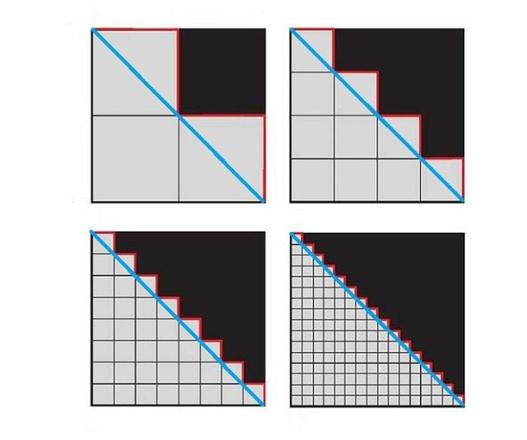
所以即使放在这个楼梯悖论中,3+4也不应该等于5,但是这么解释的话并不是所有人都能理解,因为无限多是无法直接展示出来的,全靠空间想象能力。不过即使觉得不能理解也没有关系,可以将这个有趣的3+4等于5的楼梯悖论分享给身边的朋友。或许他们会和你一样的困惑,也有可能会有更好的方法解答你心中的疑问。
以上是 为何会造成3+4等于5的困惑?3+4等于5难倒众多数学家? 的全部内容, 来源链接: utcz.com/wiki/746531.html




