IEEE-754单精度浮点数精度丢失有什么规律吗？

  • Z时代
  • 2024-02-11
  • 分类：IT

在单精度浮点数下，当我们输入的数字过大时会导致精度丢失。
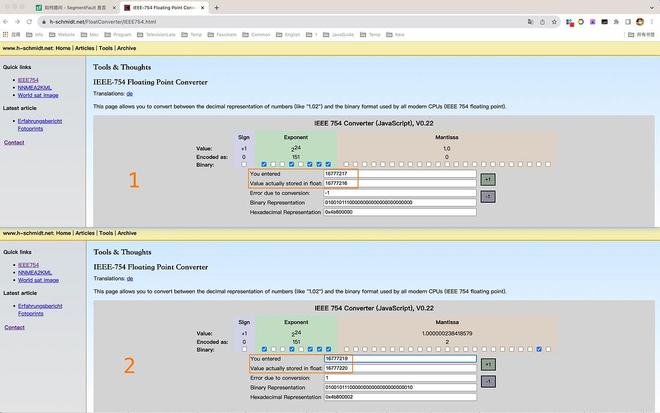
比如 输入 16777217 实际存储是 16777216；输入 16777219 实际存储 16777220。
我好奇于为什么当输入 16777217 时就是减掉1，而输入 16777219 时就是加一。

  1. 这个是对应的单精度浮点数的存储格式
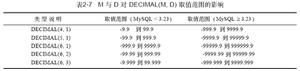
  2. 这个是我所列的转换误差的表格

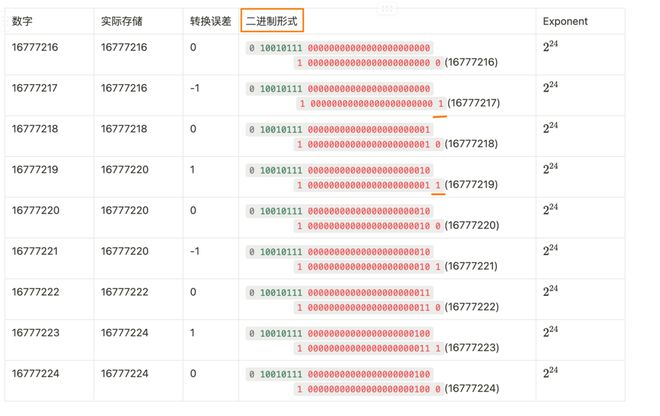
    能够看出 输入 16777217 的时候实际存储时 尾数位的第24位是直接去掉的，相当于于减一
    输入 的时候实际存储时 尾数为的第24位是在基础上加一，相当于逢二进一。

我的问题是 精度丢失是否可控？什么样趋势开始丢失精度，有没有什么规律？
换句话说就是为什么这个例子尾数位的第24位有的省略，有的则逢二进一呢？

回答：

IEEE754 定义了若干种 rounding 方案，这里用的应该是 roundTiesToEven ，就是说当两个相邻的可表示值距离实际值相等的的时候，去最末尾为偶数（对二进制来说，就是0）的那一个。

这个和四舍五入类似，只是在 .1 （相当于十进制的 .5）的时候，有时进位，有时舍去。

=======

其它的 rounding 方案还有：
roundTiesToAway 这个类似四舍五入，只要 .1 就进一
roundTowardPositive 向大的方向取整（对正数来说，就是一律进一）
roundTowardNegative 向小的方向取整
roundTowardZero 向0取整

以上是 IEEE-754单精度浮点数精度丢失有什么规律吗？ 的全部内容， 来源链接： utcz.com/p/945367.html

回到顶部