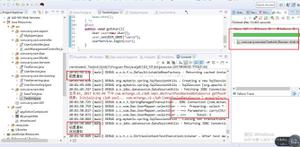
如何使用junit5,对同一测试样例不同方法进行测试?

问题背景
我有个类,里面的方法都是与排序相关的,目前想通过junit5进行测试
刚开始是考虑把测试用例直接在测试类中定义为全局变量,后面在程序中多次调用。
出现了一个问题:在运行第一个方法的时候,就会把测试用例排好序,这样导致后面的程序无法正常测试
前置代码
import java.util.Arrays;public class MySortAlgorithm_Main {
// 冒泡排序:每次从头部开始,相邻元素两两比较,每次移动其中较大那个元素
// 冒泡排序:每次从头部开始,相邻元素两两比较,每次移动其中较大那个元素
public static int[] mp_sort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
// why is "arr.length-i" ?
// Bubble sort ensures that the following elements are in order
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int z = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = z;
}
}
}
return arr;
}
// 选择排序:每次从头部开始,第一个元素看作有序序列,把第二个元素到最后一个元素看作无序序列,依次比较出序列中最小/大元素,并将其放在有序序列中
public static int[] chose_sort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
// 最小元素下标
int minIndex = i;
// why is "j=i+1" ?
// Select sort to ensure that the above elements are in order
for (int j = i + 1; j < arr.length; j++) {
// 求最小元素
if (arr[j] < arr[minIndex])
minIndex = j;
}
int z = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = z;
}
return arr;
}
// 插入排序:每次从头部开始,第一个元素看作有序序列,把第二个元素到最后一个元素看作无序序列,依次将(未排序的)元素插入到已排序序列中
public static int[] insert_sort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
// 记录需要比较的元素,即无序序列开头位置
int tmp = arr[i];
// why is "arr[j-1]" and "j=i" ?
int j = i;
while (j > 0 && arr[j - 1] > tmp) {
// 移动元素,腾出插入空间
arr[j] = arr[j - 1];
j--;
}
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
// 希尔排序:间隔分组;组内排序;……;对每组进行插入排序
public static int[] xier_sort(int[] arr) {
int length = arr.length;
int step;
int temp;
// step:进行间隔分组
for (step = length / 2; step >= 1; step /= 2) {
// 对每组进行插入排序
// 设 step=4
for (int i = step; i < length; i++) {
// arr[4]
temp = arr[i];
int j = i - step; // i=step时j=0
// 插排
while (j >= 0 && arr[j] > temp) {
arr[j + step] = arr[j];
j -= step;
}
arr[j + step] = temp;
}
}
return arr;
}
// 归并排序--递归实现
public static int[] merge_sort(int[] arr) {
// 创建临时数组
int n = arr.length;
int[] tmp = new int[n];
int left = 0;
int right = n - 1;
merge_fen(left, right, tmp, arr);
return arr;
}
private static void merge_fen(int left, int right, int[] temp, int[] arr) {
if (left < right) {
// 分
int mid = (left + right) / 2;
merge_fen(left, mid, temp, arr);
merge_fen(mid + 1, right, temp, arr);
// 并
merge_bing(left, mid, right, temp, arr);
}
}
private static void merge_bing(int left, int mid, int right, int[] temp, int[] arr) {
// 标记左半区未排序首元素
int l_post = left;
// 标记右半区未排序首元素
int r_post = mid + 1;
// 临时数组下标
int arr_index = left;
// 合并
while (l_post <= mid && r_post <= right) {
if (arr[l_post] < arr[r_post]) // 左半区<右半区
temp[arr_index++] = arr[l_post++];
else // 左半区>右半区
temp[arr_index++] = arr[r_post++];
}
// 合并左右半区剩余元素
while (l_post <= mid)
temp[arr_index++] = arr[l_post++];
while (r_post <= right)
temp[arr_index++] = arr[r_post++];
// 把临时数组中合并的元素交还给原数组
while (left <= right) {
arr[left] = temp[left];
left++;
}
}
// 快速排序:选定中心轴pivot,将大于pivot的数字放在pivot右边,将小于pivot的数字放在pivot左边,左右序列重复执行上述步骤
// 就是二分思想+基于基准数排序+递归
// 交换法
public static int[] quick_sort1(int[] arr, int left, int right) {
if (left >= right) {
return null;
}
int piv = arr[left];
int i = left;
int j = right;
while (i < j) {
// 两端不断寻找第一个小于大于piv的数
while (i < j && arr[j] >= piv)
j--;
while (i < j && arr[i] <= piv)
i++;
if (i < j) {
// 交换i和j
int z = arr[i];
arr[i] = arr[j];
arr[j] = z;
}
}
int z = arr[i];
arr[i] = arr[left];
arr[left] = z;
quick_sort1(arr, left, i - 1);
quick_sort1(arr, j + 1, right);
return arr;
}
// 挖坑法
public static int[] quick_sort2(int[] arr, int left, int right) {
if (left >= right) {
return null;
}
int piv = arr[left];
int i = left;
int j = right;
while (i < j) {
// 两端不断寻找第一个小于大于piv的数
while (i < j && arr[j] >= piv)
j--;
if (i < j)
arr[i] = arr[j];
while (i < j && arr[i] <= piv)
i++;
if (i < j)
arr[j] = arr[i];
if (i >= j)
arr[i] = piv;
}
quick_sort2(arr, left, i - 1);
quick_sort2(arr, j + 1, right);
return arr;
}
// 堆排序
// 建堆->找出堆中最大值->把它踢出堆
// 约定:堆顶元素a[0]
/**
*
* -----补充点-----
* 下标为i的节点的--
* 父节点下标:(i-1)/2
* 左孩子下标:i*2+1
* 右孩子下标:i*2+2
*
*/
public static int[] heap_sort(int[] arr, int n) {
// 建堆
// the last element of the array has index = n-1, 所以i = (index-1)/2 = n/2-1
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 排序
for (int i = n - 1; i > 0; i--) {
// 对堆顶元素进行交换
int z = arr[0];
arr[0] = arr[i];
arr[i] = z;
// 递归维护堆顶元素
heapify(arr, i, 0);
}
return arr;
}
/**
*
* @param arr 储存堆的数组
* @param n 数组长度
* @param i 待维护的元素下标
*/
// 维护堆性质
public static void heapify(int[] arr, int n, int i) {
// 父节点
int large = i;
// 左孩子&右孩子
int l_node = i * 2 + 1;
int r_node = i * 2 + 2;
if (l_node < n && arr[large] < arr[l_node])
large = l_node;
if (r_node < n && arr[large] < arr[r_node])
large = r_node;
if (large != i) {
int z = arr[i];
arr[i] = arr[large];
arr[large] = z;
heapify(arr, n, large);
}
}
/**
*
* 这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
* + 基数排序:根据键值的每位数字来分配桶;
* + 计数排序:每个桶只存储单一键值;
* + 桶排序:每个桶存储一定范围的数值;
*
*/
// 计数排序:通过计数而不是比较来进行排序,适用于范围较小的整数序列【量大且取值范围小且已知】,适用于特定问题
// 思考如果范围是100~150如何优化?----设置偏移量
// 思考如何优化成稳定排序?---- 引入累加数组,存储元素相对位置?
// 以下给出优化过后的代码
public static int[] countSort(int[] arr) {
int temp[] = new int[arr.length];
int max = arr[0], min = arr[0];
for (int i : arr) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
} // 这里k的大小是要排序的数组中,元素大小的极值差+1
int k = max - min + 1;
int c[] = new int[k];
for (int i = 0; i < arr.length; ++i) {
c[arr[i] - min] += 1;// 优化过的地方,减小了数组c的大小
}
for (int i = 1; i < c.length; ++i) {
c[i] = c[i] + c[i - 1];
}
for (int i = arr.length - 1; i >= 0; --i) {
temp[--c[arr[i] - min]] = arr[i];// 按存取的方式取出c的元素
}
return temp;
}
// 基数排序1[马士兵版本]
public static int[] radix_sort1(int[] arr, int radix) {
int[] result = new int[arr.length]; // 结果数组
int[] cnt = new int[10];// 每一位都是由 0~9 共10位数组成
for (int i = 0; i < radix; i++) {
// 每一轮获取低位
int division = (int) Math.pow(10, i);// 求10^i 第一轮取所有数组元素个位,第二轮取所有数组元素十位,以此类推直至最高位
for (int j = 0; j < arr.length; j++) {
int num = arr[j] / division % 10; // arr[j]/division:每次取num截断位;上述%10获取个数,注意这里的10是基数
cnt[num]++;
}
for (int m = 1; m < cnt.length; m++)
cnt[m] = cnt[m] + cnt[m - 1];
for (int n = arr.length - 1; n >= 0; n--) {
int elem = arr[n] / division % 10;// 同上
// int elem = arr[n];
result[--cnt[elem]] = arr[n];
}
// 以下代码不可少
System.arraycopy(result, 0, arr, 0, arr.length); // Copies an array from the specified source array, beginning at
// the specified position, to the specified position of the
// destination array.
Arrays.fill(cnt, 0); // Assigns the specified value to each element of the specified range of the
// specified array.
}
return result;
}
// 基数排序2[百度百科版本]
public static int[] radix_sort2(int[] arr, int radix) {
int k = 0;
int n = 1;
int m = 1; // 控制键值排序依据在哪一位
int[][] temp = new int[10][arr.length]; // 数组的第一维表示可能的余数0-9
int[] order = new int[10]; // 数组order[i]用来表示该位是i的数的个数
while (m <= radix) {
for (int i = 0; i < arr.length; i++) {
int lsd = ((arr[i] / n) % 10);
temp[lsd][order[lsd]] = arr[i];
order[lsd]++;
}
for (int i = 0; i < 10; i++) {
if (order[i] != 0)
for (int j = 0; j < order[i]; j++) {
arr[k] = temp[i][j];
k++;
}
order[i] = 0;
}
n *= 10;
k = 0;
m++;
}
return arr;
}
// 桶排序
public static int[] basket_sort(int arr[]) {
int n = arr.length;
int bask[][] = new int[10][n];
int index[] = new int[10];
int max = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
max = max > (Integer.toString(arr[i]).length()) ? max : (Integer.toString(arr[i]).length());
}
String str;
for (int i = max - 1; i >= 0; i--) {
for (int j = 0; j < n; j++) {
str = "";
if (Integer.toString(arr[j]).length() < max) {
for (int k = 0; k < max - Integer.toString(arr[j]).length(); k++)
str += "0";
}
str += Integer.toString(arr[j]);
bask[str.charAt(i) - '0'][index[str.charAt(i) - '0']++] = arr[j];
}
int pos = 0;
for (int j = 0; j < 10; j++) {
for (int k = 0; k < index[j]; k++) {
arr[pos++] = bask[j][k];
}
}
for (int x = 0; x < 10; x++)
index[x] = 0;
}
return arr;
}
}
问题代码
import algorithm.sort_.MySortAlgorithm_Main;import org.junit.jupiter.api.*;
@TestInstance(TestInstance.Lifecycle.PER_CLASS)
public class Sort_Test3 {
private final int[] testData = init_All();
private int[] runTest_Data;
int[] init_All(){
final int[] testData;
System.out.println("before run...");
// 随机生成测试数据
int n = (int) (Math.random() * 1000);
System.out.println(n);
testData = new int[n];
for (int i = 0; i < n; i++) {
testData[i] = (int) (Math.random() * 1000);
}
return testData;
}
@BeforeAll
void print(){
System.out.println();
System.out.println("--------------程序运行结束--------------");
}
@BeforeEach
void init_(){
this.runTest_Data = testData;
System.out.println("run...");
}
@AfterEach
void space() {
System.out.println();
}
@Test
//冒泡排序
public void test_mpSort() {
for (int i:testData) {
System.out.println(i);
}
int[] mp = MySortAlgorithm_Main.mp_sort(testData);
System.out.println("冒泡排序结果:");
}
@Test
// 选择排序
void test_choseSort() {
for (int i:testData) {
System.out.println(i);
}
int[] cos = MySortAlgorithm_Main.chose_sort(testData);
System.out.println("选择排序结果:");
}
@Test
// 插入排序
void test_insertSort() {
for (int i:testData) {
System.out.println(i);
}
int[] ins = MySortAlgorithm_Main.insert_sort(testData);
System.out.println("插入排序结果");
}
}
需求描述
我现在需要实现:
- 测试用例不要重复输入
- 单次的所有测试方法共用同一测试用例
请问大佬们应当如何实现
回答:
@BeforeEach就是在当前类中的每个@Test之前做的事情。
@BeforeEachvoid init_(){
this.runTest_Data = init_All(); // 每次之前前,都重新生成测试数据
System.out.println("run...");
}
然后把后面的测试数据把testData都改成runTest_Data就行了。
本文参与了SegmentFault 思否面试闯关挑战赛,欢迎正在阅读的你也加入。
回答:
再现一个打乱排序的方法, 然后确保调用每个测试方法前执行一遍
以上是 如何使用junit5,对同一测试样例不同方法进行测试? 的全部内容, 来源链接: utcz.com/p/945038.html