算法问题:鸡块有 7/13/29 三种规格,老板让你买 n 块,如何计算是否可行
问题:在一个平行宇宙中,麦当劳的麦乐鸡块分为 7 块装、13 块装和 29 块装。有一天,你的老板让你出去购买正好为 n 块(0 < n <= 10000)的麦乐鸡块回来,请提供一个算法判断是否可行。
说明:除了三重循环的解法,有没有效率更高一点的方法。求大佬指点。
回答:
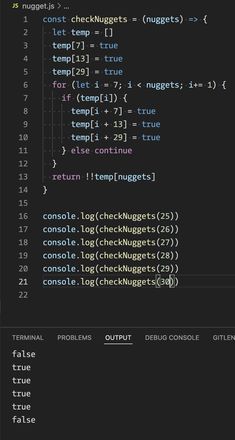
const checkNuggets = (nuggets) => { let temp = []
temp[7] = true
temp[13]-= true
temp[29] = true
for (let i = 7; i < nuggets; i+= 1) {
if (temp[i]) {
temp[i + 7] = true
temp[i + 13] = true
temp[i + 29] = true
} else continue
}
return !!temp[nuggets]
}
console.log(checkNuggets(25)) // false
console.log(checkNuggets(26)) // true
console.log(checkNuggets(27)) // true
console.log(checkNuggets(28)) // true
console.log(checkNuggets(29)) // true
console.log(checkNuggets(30)) // false
回答:
取巧的一个思路,反正 n块(0< n <= 10000)
- 直接拿到 0-10000 里 7,13,29 所有可能构成的取值,建立哈希表,结束了
- 效率肯定很高
回答:
function countAll(i, j, k, total) { if ((i * 7 + j * 13 + 29 * k) > total) {
return false;
}
if (total === 7 || total === 13 || total === 29) {
return true;
}
if (isVoid(i, j, k, total)) {
return true;
} else {
return countAll(i, j, k + 1 , total) || countAll(i , j + 1, k , total) || countAll(i + 1, j , k , total) || false;
}
}
function isVoid(i, j, k, total) {
let value = i * 7 + j * 13 + 29 * k;
if (total % value == 0 && value !== 0) {
console.log(i , j , k);
return true;
}
return false;
}
var res = countAll(0, 0 , 0 ,9892);
console.log(res);
递归实现
回答:
范围内枚举
在范围内进行枚举,将中间过程存入桶。具体的,桶的初始值默认为 0,接下来进行递归:
bool resBucket[10005]; // 范围为 1~10000bool check ( ) {
memset (resBucket, 0, sizeof (resBucket)); // 默认为 false
queue <int> q; // 队列里存入所有合理的数
q.push (0); // 一个不买显然合理
while (!q.empty ( )) { // 当有待查验的数时:
int tmp = q.front ( ); q.pop ( ); // 记录现在处理的合理的数
if (tmp > n) continue; // 越界,无需查验
if (tmp == n) return true; // 可行,结束
if (resBucket[tmp] == true) continue; // 重复,无需再枚举
resBucket[tmp] = true; // 记录
q.push (tmp + 7); q.push (tmp + 13); q.push (tmp + 29);
// 若 tmp 可以,多买这三种中任何一个都可以
}
return false; // 所有可行方案全遍历过了,不可行,结束
}
以上是 算法问题:鸡块有 7/13/29 三种规格,老板让你买 n 块,如何计算是否可行 的全部内容, 来源链接: utcz.com/p/944378.html