sympy求解方程组符号解?
有一组比较复杂的符号方程组想要求解,基本模型大概是这样: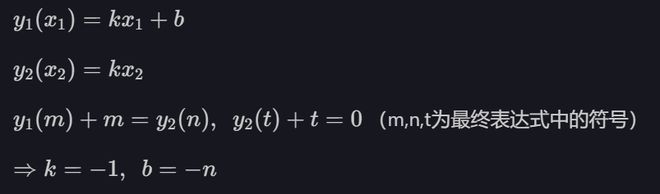
在sympy里使用Function表示\(y_1\)和\(y_2\),但是怎么把方程里的\(kx_1+b\)和\(kx_2\)代入函数里面?
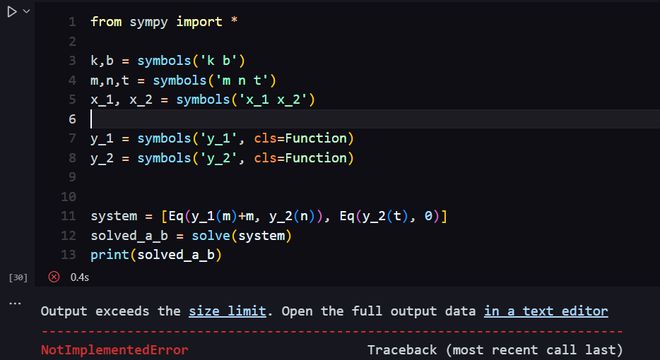
from sympy import *k,b = symbols('k b')
m,n,t = symbols('m n t')
x_1, x_2 = symbols('x_1 x_2')
y_1 = symbols('y_1', cls=Function)
y_2 = symbols('y_2', cls=Function)
system = [Eq(y_1(m), y_2(n)), Eq(y_2(t), 0)]
solved_a_b = solve(system)
print(solved_a_b)
回答:
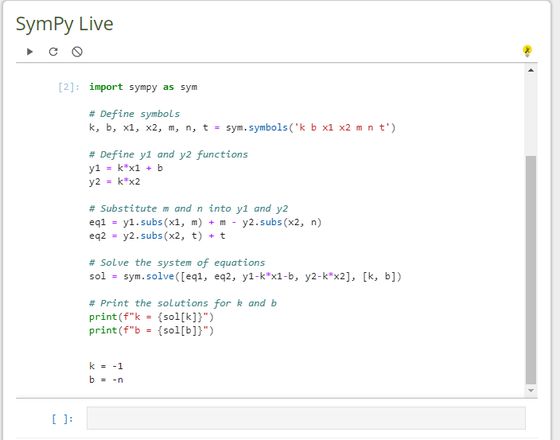
import sympy as sym# Define symbols
k, b, x1, x2, m, n, t = sym.symbols('k b x1 x2 m n t')
# Define y1 and y2 functions
y1 = k*x1 + b
y2 = k*x2
# Substitute m and n into y1 and y2
eq1 = y1.subs(x1, m) + m - y2.subs(x2, n)
eq2 = y2.subs(x2, t) + t
# Solve the system of equations
sol = sym.solve([eq1, eq2, y1-k*x1-b, y2-k*x2], [k, b])
# Print the solutions for k and b
print(f"k = {sol[k]}")
print(f"b = {sol[b]}")
回答:
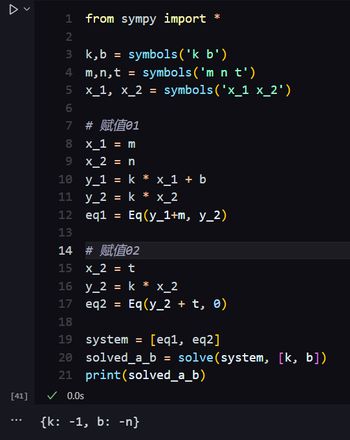
大伙们我会了。每变一次自变量就重新代入一次就行:
from sympy import *k,b = symbols('k b')
m,n,t = symbols('m n t')
x_1, x_2 = symbols('x_1 x_2')
# 赋值01
x_1 = m
x_2 = n
y_1 = k * x_1 + b
y_2 = k * x_2
eq1 = Eq(y_1+m, y_2)
# 赋值02
x_2 = t
y_2 = k * x_2
eq2 = Eq(y_2 + t, 0)
system = [eq1, eq2]
solved_a_b = solve(system, [k, b])
print(solved_a_b)
以上是 sympy求解方程组符号解? 的全部内容, 来源链接: utcz.com/p/938775.html