随机数种子的意思?

我注意到在多种语言中,随机数的生成有一个随机数种子的概念,如果使用不当,将可能生成相同的随机数,例如:
使用go生成一个随机字符串:
const letterBytes = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"func randomString(n int) string {
b := make([]byte, n)
// [1]
// rand.Seed(time.Now().Unix()) 打开此处得到正确的随机数
for i := range b {
// [2]
// rand.Seed(time.Now().Unix()) 打开此处每次得到相同的随机数
b[i] = letterBytes[rand.Intn(len(letterBytes))]
}
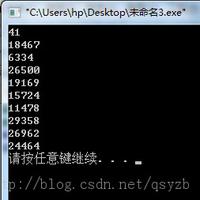
//打开【2】得到类似 [71 71 71 71 71 71 71 71 71 71]的相同结果
//打开【1】得到类似 [75 111 79 115 101 73 120 66 71 83]的正常结果
fmt.Println(b)
return string(b)
}
func main() {
s := randomString(10)
fmt.Println(s)
}
我知道如何得到正确的随机数,但我并不清楚随机数生成如何基于或者依赖于随机数种子,请问有人能 简单通俗 的说明一下 随机数种子如何工作吗?
回答:
原因非常简单,世界上的一切都是有规律的,不存在任何无规律的事情。包括量子力学也是有规律的。
y=func(x)
只要 x 确定,y 就一定确定。所以计算机世界是不存在随机数的。
但是可以做到乍一看是随机的,怎么实现呢?就是不停的换 x ,自然 y 就变了。那 x 可以取什么?当然就是时间了。
计算机的时间从哪里来?从晶体振荡器来。
当然,还可以取CPU频率、CPU温度等等来作为随机数种子
回答:
简单来说:
随机是什么?随机就是一个不可预测、没有根据的行为。
传统的冯诺依曼架构计算机,它只是按照人所下达的指令,即按照程序来机械性地执行一些计算,所以它的行为是可预测的,违背了随机的定义。故,我们把传统计算机所生成的“随机数”称为伪随机数。
由此可知,伪随机是可预测,有根据的。那么生成这个伪随机数的根据,我们称之为随机数种子,再在这个种子数值上进行一系列复杂的计算,我们得到了所谓的伪随机数。所生成的数值随种子的变化而变化,种子一个微小的变动,在经过复杂计算后得到的值与原先的数值大相径庭;若不变化种子则生成的随机数也不会变化。我们在设计程序时一般把不断自增的时间戳作为随机数种子。
另外,随着量子力学理论的不断完善,量子计算机得以用物理方法产生真随机数,但其可预测性、是否有根据就要留给物理界讨论了。
回答:
普通的程序语言中,随机数都是伪随机数(序列),
它有好处和坏处,
好处是调试程序时,用固定的种子,会产生相同的序列,方便程序的调试;
坏处是这个不是真正的随机数,如果需要真正的随机数,就需要增加随机数种子,而且每次获取时都要用新的随机数种子,其实这里的随机数种子才是相对随机的东东(但可能不满足随机数取值条件)。
现在有些系统中有真正的随机数发生器,可以更好的获取随机数。
至于随机数种子的作用,其实是因为很多语言中伪随机数发生器实质是一个基于大质数处理的伪随机数序列发生器,这种发生器对相同的种子产生相同的序列,所以如果种子是随机的,相当于获取了一个随机的序列。
以上是 随机数种子的意思? 的全部内容, 来源链接: utcz.com/p/938275.html