java图搜索算法之图的对象化描述示例详解

  • Z时代
  • 2024-01-10
  • 分类：IT

你好，我是小黄，一名独角兽企业的Java开发工程师。

校招收获数十个offer，年薪均20W~40W。

感谢茫茫人海中我们能够相遇，

俗话说：当你的才华和能力，不足以支撑你的梦想的时候，请静下心来学习，

希望优秀的你可以和我一起学习，一起努力，实现属于自己的梦想。

一、前言

对于图来说，我一直以来都似懂非懂

懂的是图的含义，不懂的是图具体的实现

对于当前各大厂面试的图题，不外乎以下几点：

深度优先搜索、广度优先搜索：DFS、BFS最小生成树：Kruskal、Prim最短路径：Dijkstra、Dijkstra加强堆版拓扑排序：TopologicalSort

这几个算法其实听起来不太难懂，但真正写代码的时候会发现一个事情，傻逼图的边和点太难描述，导致我们写着写着人就没了，绕进去出不来了

本篇系列文章，将从对象的角度来描述一个图的产生，并用最简单的思路去介绍上述所有算法，让我们走进本篇文章吧。

二、什么是图

图是我们现实生活中连接关系的抽象，例如朋友圈、微博的关注关系。

简单抽象如下图所示：

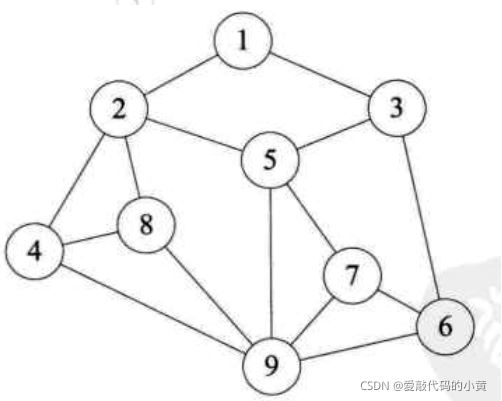
在这里插入图片描述

对于图来说，分为有向图和无向图，如下图所示：

在这里插入图片描述

我们可以看出来，有向图代表只能从一个顶点到达另一个顶点，而无向图代表两个顶点之间可以相互到达。

图1中，V4到达V1，而V1无法到达V4

图2中，V4到达V1，V1也可以到达V4

当然，还有一种图的形式，叫做：带权图（主要用来做一些路程、路费的计算），如下图所示：

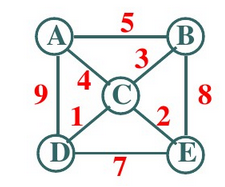
在这里插入图片描述

三、怎么存储一个图的结构

我们在刷题的时候，题目给我们的样例经常是这种的：743. 网络延迟时间

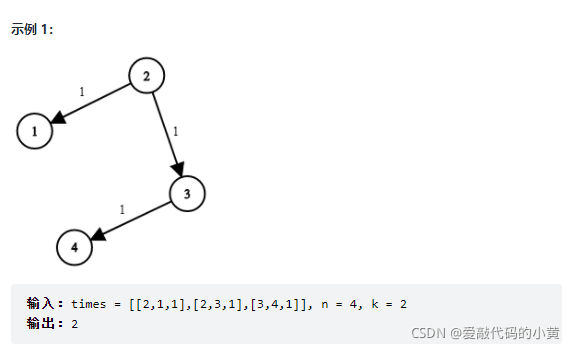
在这里插入图片描述

题目会给我们一个二维的矩阵，一行矩阵有三个数字，分别是：起始点、终止点、权重

如何将这个二维的矩阵表示出来，成为了我们在做图题目中比较困难的一件事

本文将直接使用一种特殊的表示形式来解决这个难题，我们先从最基本的 邻接矩阵 和 邻接表 表示开始

1、邻接矩阵

邻接矩阵是表示图中顶点之间相邻关系的矩阵。

对于无向图的邻接矩阵：对称矩阵：int[][]

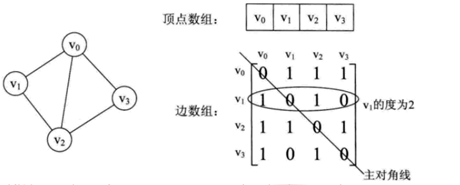
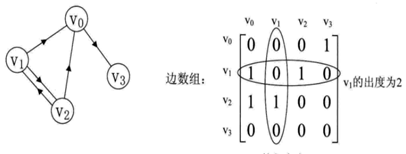
在这里插入图片描述

有向图的邻接矩阵：各行之和是出度，各列之和是入度

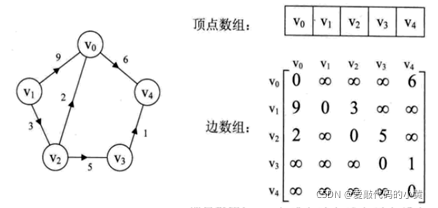
在这里插入图片描述

带权图的邻接矩阵

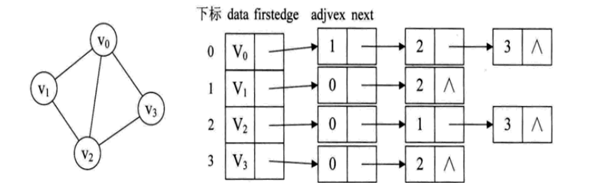
在这里插入图片描述

2、邻接表

邻接表是一种链式存储结构，类似于链表数组。

无向图的邻接表：HashMap<Integer, ArrayList<Integer>>

在这里插入图片描述

3、图对象化表示

我们思考，上述两个方法对于图的表示形象嘛？

虽然有的题目在用矩阵表示的时候，做起来很舒服，但我们想一想，当我们求最小生成树时，利用边的连接解锁点时，用矩阵会

不会感觉很抽象难懂，所示，我们要自定义一个图的表示方法，来增强我们对图的理解

对于图来说，我们想一想主要包括什么？

图是由点和边组成的一个结构，也就是我们想要勾画一个图，必须有：点、边

点的描述：

点的值：int value

邻接的点：ArrayList<Node> nexts

邻接的边：ArrayList<Edge> edges

入度：int in

出度：int out

public class Node {
    public int value;
    public int in;
    public int out;
    public ArrayList<Node> nexts;
    public ArrayList<Edge> edges;
    public Node(int value) {
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

边的描述：

来自哪里：Node from去往哪里：Node to边的权重：int weight

public class Edge {
    Node from;
    Node to;
    int weight;
    public Edge(Node from, Node to, int weight) {
        this.from = from;
        this.to = to;
        this.weight = weight;
    }
}

图的描述：

多个点的集合：HashMap<Integer, Node> nodes多个边的集合：Set<Edge> edges

public class Graph {
    public HashMap<Integer, Node> nodes;
    public Set<Edge> edges;
    public Graph() {
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

这里可能有疑问了，你这样写虽然形象，但是怎么进行转化呢？

别急，下面我们就进行转化。

public static Graph createGraph(int[][] matrix) {
        // 初始化一个图
        Graph graph = new Graph();
        for (int[] arr : matrix) {
            // 来的点
            int from = arr[0];
            // 去的点
            int to = arr[1];
            // 权重
            int value = arr[2];
            // 生成相对应的点
            Node fromNode = new Node(from);
            Node toNode = new Node(to);
            // 查看当前有没有这个点的信息
            if (!graph.nodes.containsKey(from)) {
                graph.nodes.put(from, fromNode);
            }
            if (!graph.nodes.containsKey(to)) {
                graph.nodes.put(to, toNode);
            }
            // 生成一个边(这里的边是有向边)
            Edge edge = new Edge(fromNode, toNode, value);
            // 点里面加入边
            graph.nodes.get(from).edges.add(edge);
            //  点里面加入下一个点
            graph.nodes.get(from).nexts.add(toNode);
            // 点里面加入入度和出度
            graph.nodes.get(from).out++;
            graph.nodes.get(to).in++;
            // 图里面加入边
            graph.edges.add(edge);
        }
        return graph;
    }

当我们转化完的时候，进行测试：

public static void main(String[] args) {
        int[][] arr = new int[][]{{2, 1, 1}, {2, 3, 1}, {3, 4, 1}};
        Graph graph = createGraph(arr);
        // 从2开始的边有哪些
        List<Edge> edgeList = graph.nodes.get(2).edges;
        for (Edge edge : edgeList) {
            System.out.println("从" + edge.from.value + "---->" + edge.to.value + "权值为" + edge.weight);
        }
    }

最终结果：

从2---->1权值为1

从2---->3权值为1

以后我们在做题的时候，都可以保存此转化代码，直接进行调用即可

简单形象的描绘了我们的图

四、图的作用

图经常用在以下地方：

  • 深度优先搜索、广度优先搜索：DFS、BFS

  • 最小生成树：Kruskal、Prim

  • 最短路径：Dijkstra、Dijkstra加强堆版

  • 拓扑排序：TopologicalSort

之后的章节会慢慢的讲解以上所有的应用

在这里插入图片描述

以上就是java算法图的对象化描述示例详解的详细内容，更多关于java图的对象化描述算法的资料请关注其它相关文章！

以上是 java图搜索算法之图的对象化描述示例详解 的全部内容， 来源链接： utcz.com/p/250572.html

回到顶部