Java基于栈方式解决汉诺塔问题实例【递归与非递归算法】
本文实例讲述了Java基于栈方式解决汉诺塔问题。分享给大家供大家参考,具体如下:
/**
* 栈方式非递归汉诺塔
* @author zy
*
*/
public class StackHanoi
{
/**
* @param args
*/
public static void main(String[] args)
{
System.out.println("测试结果:");
System.out.println("递归方式:");
hanoiNormal(3, 'A', 'B', 'C');
System.out.println();
System.out.println("非递归方式:");
hanoi(3, 'A', 'B', 'C');
}
/**
* 递归汉诺塔
* @param n
* @param A
* @param B
* @param C
*/
public static void hanoiNormal(int n, char A, char B, char C)
{
//hanoiNormal(1, A, B, C)等价于直接移动A到C( move(A,C) )
if(n==1)
{
move(A, C);
return;
}
else
{
hanoiNormal(n-1, A, C, B);
move(A, C);
hanoiNormal(n-1, B, A, C);
}
}
/**
* 非递归汉诺塔
* @param n
* @param A
* @param B
* @param C
*/
public static void hanoi(int n, char A, char B, char C)
{
//创建一个栈
StateStack s = new StateStack();
//将开始状态进栈
s.push( new State(n, A, B, C) );
//保存出栈元素
State state = null;
//出栈
while((state = s.pop()) != null)
{
//如果n为1( hanoi(1,A,B,C) ),直接移动A->C
if(state.n == 1)
{
move(state.A, state.C);
}
//如果n大于1,则按照递归的思路,先处理hanoi(n-1,A,C,B),再移动A->C(等价于hanoi(1,A,B,C) ),然后处理hanoi(n-1,B,A,C),因为是栈,所以要逆序添加
else
{
//栈结构先进后出,所以需要逆序进栈
s.push( new State(state.n-1, state.B, state.A, state.C) );
s.push( new State(1, state.A, state.B, state.C) );
s.push( new State(state.n-1, state.A, state.C, state.B) );
}
}
}
/**
* 从s到d移动盘子
*/
public static void move(char s, char d)
{
System.out.println(s+"->"+d);
}
}
//状态
class State
{
public int n;
public char A;
public char B;
public char C;
public State(int n, char A, char B, char C)
{
this.n = n;
this.A = A;
this.B = B;
this.C = C;
}
}
//栈
class StateStack
{
private State[] storage = new State[1000];
//栈顶
private int top = 0;
//入栈
public void push(State s)
{
storage[top++] = s;
}
//出栈
public State pop()
{
if(top>0)
{
return storage[--top];
}
return null;
}
}
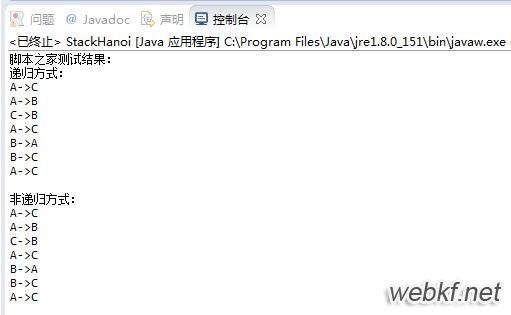
运行结果:
以上是 Java基于栈方式解决汉诺塔问题实例【递归与非递归算法】 的全部内容, 来源链接: utcz.com/p/214905.html