Java经典排序算法之二分插入排序详解
一、折半插入排序(二分插入排序)
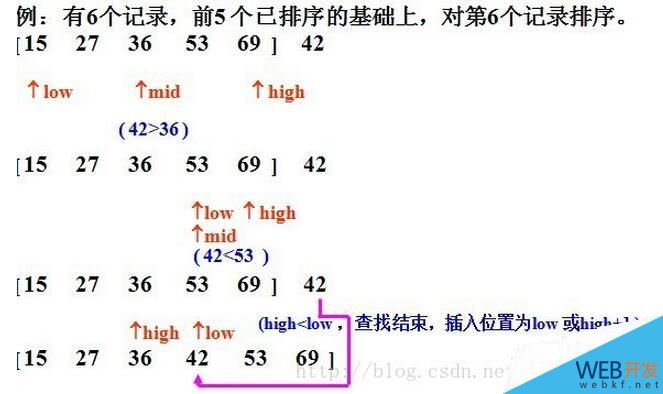
将直接插入排序中寻找A[i]的插入位置的方法改为采用折半比较,即可得到折半插入排序算法。在处理A[i]时,A[0]……A[i-1]已经按关键码值排好序。所谓折半比较,就是在插入A[i]时,取A[i-1/2]的关键码值与A[i]的关键码值进行比较,如果A[i]的关键码值小于A[i-1/2]的关键码值,则说明A[i]只能插入A[0]到A[i-1/2]之间,故可以在A[0]到A[i-1/2-1]之间继续使用折半比较;否则只能插入A[i-1/2]到A[i-1]之间,故可以在A[i-1/2+1]到A[i-1]之间继续使用折半比较。如此担负,直到最后能够确定插入的位置为止。一般在A[k]和A[r]之间采用折半,其中间结点为A[k+r/2],经过一次比较即可排除一半纪录,把可能插入的区间减小了一半,故称为折半。执行折半插入排序的前提是文件纪录必须按顺序存储。
二、算法原理
折半插入排序的算法思想:
算法的基本过程:
(1)计算 0 ~ i-1 的中间点,用 i 索引处的元素与中间值进行比较,如果 i 索引处的元素大,说明要插入的这个元素应该在中间值和刚加入i索引之间,反之,就是在刚开始的位置 到中间值的位置,这样很简单的完成了折半;
(2)在相应的半个范围里面找插入的位置时,不断的用(1)步骤缩小范围,不停的折半,范围依次缩小为 1/2 1/4 1/8 .......快速的确定出第 i 个元素要插在什么地方;
(3)确定位置之后,将整个序列后移,并将元素插入到相应位置。
三、代码实现
public class BinarySort {
public static void binarySort(int[] source) {
int i, j;
int high, low, mid;
int temp;
for (i = 1; i < source.length; i++) {
// 查找区上界
low = 0;
// 查找区下界
high = i - 1;
//将当前待插入记录保存在临时变量中
temp = source[i];
while (low <= high) {
// 找出中间值
// mid = (low + high) / 2;
mid = (low + high) >> 1;
//如果待插入记录比中间记录小
if (temp<source[mid] ) {
// 插入点在低半区
high = mid - 1;
} else {
// 插入点在高半区
low = mid + 1;
}
}
//将前面所有大于当前待插入记录的记录后移
for (j = i - 1; j >=low; j--) {
source[j + 1] = source[j];
}
//将待插入记录回填到正确位置.
source[low] = temp;
System.out.print("第" + i + "趟排序:");
printArray(source);
}
}
private static void printArray(int[] source) {
for (int i = 0; i < source.length; i++) {
System.out.print("\t" + source[i]);
}
System.out.println();
}
public static void main(String[] args) {
int source[] = new int[] { 12, 15, 9, 14, 4, 18, 23, 6 };
System.out.print("初始关键字:");
printArray(source);
System.out.println("");
binarySort(source);
System.out.print("\n\n排序后结果:");
printArray(source);
}
}
四、运行结果
初始关键字: 12 15 9 14 4 18 23 6
第1趟排序: 12 15 9 14 4 18 23 6
第2趟排序: 9 12 15 14 4 18 23 6
第3趟排序: 9 12 14 15 4 18 23 6
第4趟排序: 4 9 12 14 15 18 23 6
第5趟排序: 4 9 12 14 15 18 23 6
第6趟排序: 4 9 12 14 15 18 23 6
第7趟排序: 4 6 9 12 14 15 18 23
排序后结果: 4 6 9 12 14 15 18 23
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持。
以上是 Java经典排序算法之二分插入排序详解 的全部内容, 来源链接: utcz.com/p/212012.html