简单介绍线性表以及如何实现双链表
线性表是一种线性结构,它是具有相同类型的n(n≥0)个数据元素组成的有限序列。
一、数组
数组有上界和下界,数组的元素在上下界内是连续的。
存储10,20,30,40,50的数组的示意图如下:
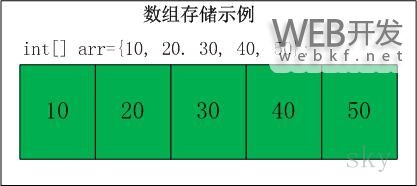
数组的特点:数据是连续的;随机访问速度快。
数组中稍微复杂一点的是多维数组和动态数组。对于C语言而言,多维数组本质上也是通过一维数组实现的。至于动态数组,是指数组的容量能动态增长的数组;对于C语言而言,若要提供动态数组,需要手动实现;而对于C++而言,STL提供了Vector;对于Java而言,Collection集合中提供了ArrayList和Vector。
二、单向链表
单向链表(单链表)是链表的一种,它由节点组成,每个节点都包含下一个节点的指针。
单链表的示意图如下:
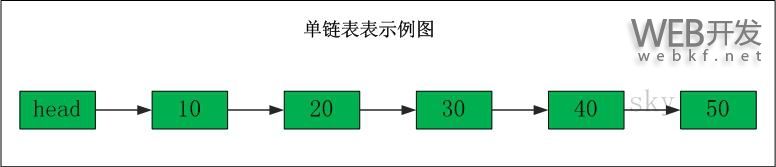
表头为空,表头的后继节点是"节点10"(数据为10的节点),"节点10"的后继节点是"节点20"(数据为10的节点),...
单链表删除节点
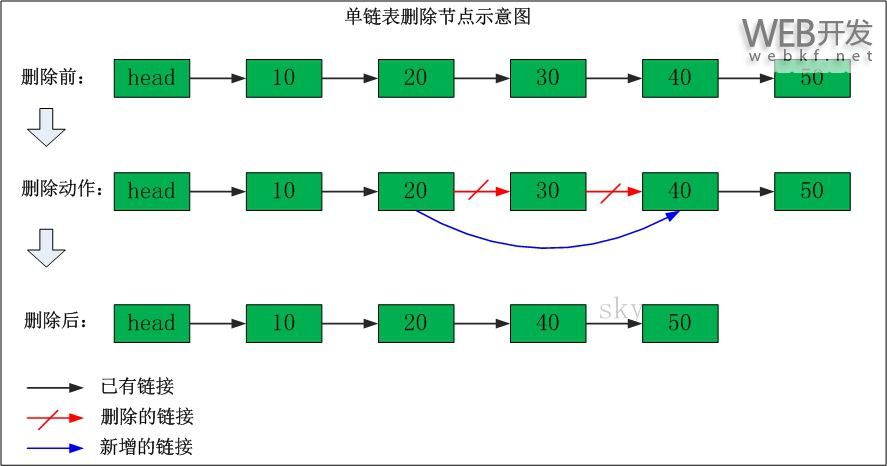
删除"节点30"
删除之前:"节点20" 的后继节点为"节点30",而"节点30" 的后继节点为"节点40"。
删除之后:"节点20" 的后继节点为"节点40"。
单链表添加节点
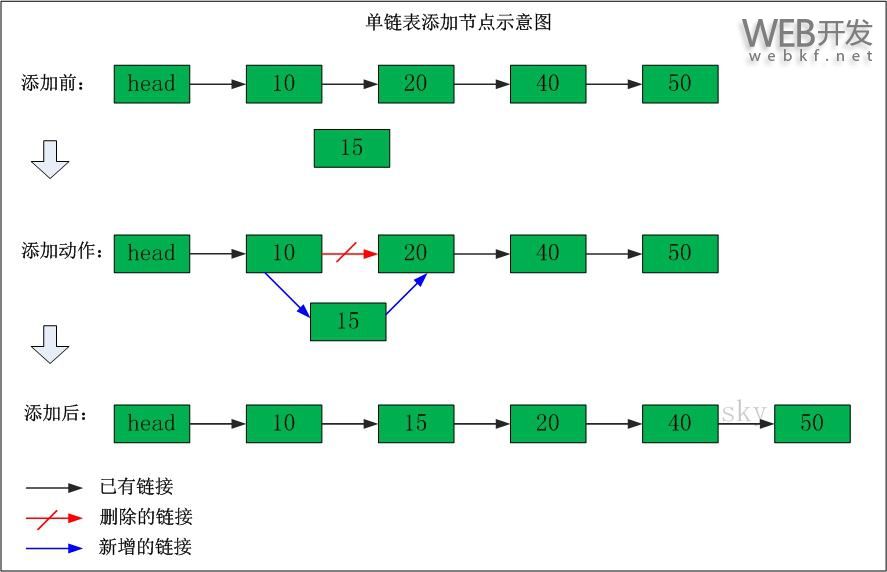
在"节点10"与"节点20"之间添加"节点15"
添加之前:"节点10" 的后继节点为"节点20"。
添加之后:"节点10" 的后继节点为"节点15",而"节点15" 的后继节点为"节点20"。
单链表的特点是:节点的链接方向是单向的;相对于数组来说,单链表的的随机访问速度较慢,但是单链表删除/添加数据的效率很高。
三、双向链表
双向链表(双链表)是链表的一种。和单链表一样,双链表也是由节点组成,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
双链表的示意图如下:

表头为空,表头的后继节点为"节点10"(数据为10的节点);"节点10"的后继节点是"节点20"(数据为10的节点),"节点20"的前继节点是"节点10";"节点20"的后继节点是"节点30","节点30"的前继节点是"节点20";...;末尾节点的后继节点是表头。
双链表删除节点

删除"节点30"
删除之前:"节点20"的后继节点为"节点30","节点30" 的前继节点为"节点20"。"节点30"的后继节点为"节点40","节点40" 的前继节点为"节点30"。
删除之后:"节点20"的后继节点为"节点40","节点40" 的前继节点为"节点20"。
双链表添加节点
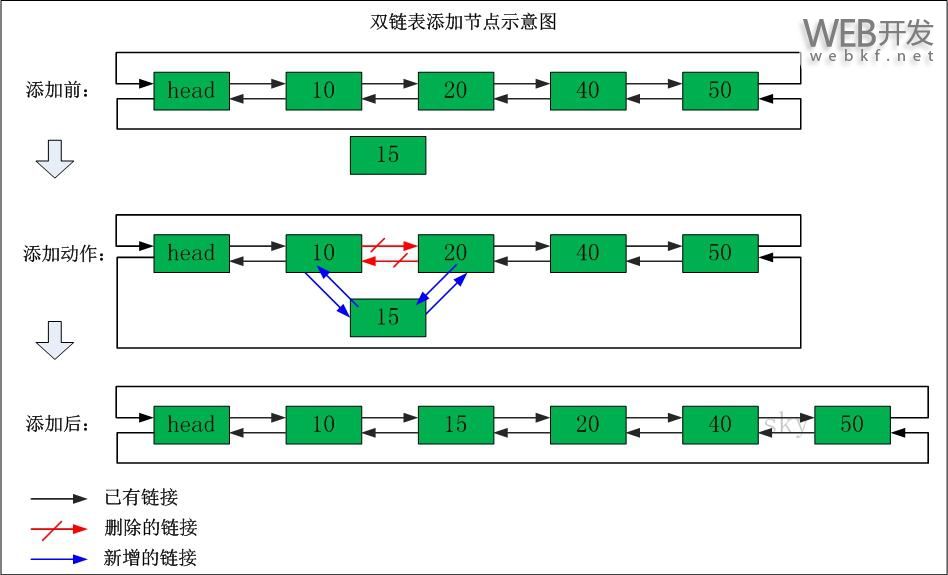
在"节点10"与"节点20"之间添加"节点15"
添加之前:"节点10"的后继节点为"节点20","节点20" 的前继节点为"节点10"。
添加之后:"节点10"的后继节点为"节点15","节点15" 的前继节点为"节点10"。"节点15"的后继节点为"节点20","节点20" 的前继节点为"节点15"。
下面介绍双链表的实现,分别介绍C/C++/Java三种实现。
1. C实现双链表
实现代码
双向链表头文件(double_link.h)
#ifndef _DOUBLE_LINK_H
#define _DOUBLE_LINK_H
// 新建“双向链表”。成功,返回表头;否则,返回NULL
extern int create_dlink();
// 撤销“双向链表”。成功,返回0;否则,返回-1
extern int destroy_dlink();
// “双向链表是否为空”。为空的话返回1;否则,返回0。
extern int dlink_is_empty();
// 返回“双向链表的大小”
extern int dlink_size();
// 获取“双向链表中第index位置的元素”。成功,返回节点指针;否则,返回NULL。
extern void* dlink_get(int index);
// 获取“双向链表中第1个元素”。成功,返回节点指针;否则,返回NULL。
extern void* dlink_get_first();
// 获取“双向链表中最后1个元素”。成功,返回节点指针;否则,返回NULL。
extern void* dlink_get_last();
// 将“value”插入到index位置。成功,返回0;否则,返回-1。
extern int dlink_insert(int index, void *pval);
// 将“value”插入到表头位置。成功,返回0;否则,返回-1。
extern int dlink_insert_first(void *pval);
// 将“value”插入到末尾位置。成功,返回0;否则,返回-1。
extern int dlink_append_last(void *pval);
// 删除“双向链表中index位置的节点”。成功,返回0;否则,返回-1
extern int dlink_delete(int index);
// 删除第一个节点。成功,返回0;否则,返回-1
extern int dlink_delete_first();
// 删除组后一个节点。成功,返回0;否则,返回-1
extern int dlink_delete_last();
#endif
双向链表实现文件(double_link.c)
#include <stdio.h>
#include <malloc.h>
/**
* C 语言实现的双向链表,能存储任意数据。
*
* @author skywang
* @date 2013/11/07
*/
// 双向链表节点
typedef struct tag_node
{
struct tag_node *prev;
struct tag_node *next;
void* p;
}node;
// 表头。注意,表头不存放元素值!!!
static node *phead=NULL;
// 节点个数。
static int count=0;
// 新建“节点”。成功,返回节点指针;否则,返回NULL。
static node* create_node(void *pval)
{
node *pnode=NULL;
pnode = (node *)malloc(sizeof(node));
if (!pnode)
{
printf("create node error!\n");
return NULL;
}
// 默认的,pnode的前一节点和后一节点都指向它自身
pnode->prev = pnode->next = pnode;
// 节点的值为pval
pnode->p = pval;
return pnode;
}
// 新建“双向链表”。成功,返回0;否则,返回-1。
int create_dlink()
{
// 创建表头
phead = create_node(NULL);
if (!phead)
return -1;
// 设置“节点个数”为0
count = 0;
return 0;
}
// “双向链表是否为空”
int dlink_is_empty()
{
return count == 0;
}
// 返回“双向链表的大小”
int dlink_size() {
return count;
}
// 获取“双向链表中第index位置的节点”
static node* get_node(int index)
{
if (index<0 || index>=count)
{
printf("%s failed! index out of bound!\n", __func__);
return NULL;
}
// 正向查找
if (index <= (count/2))
{
int i=0;
node *pnode=phead->next;
while ((i++) < index)
pnode = pnode->next;
return pnode;
}
// 反向查找
int j=0;
int rindex = count - index - 1;
node *rnode=phead->prev;
while ((j++) < rindex)
rnode = rnode->prev;
return rnode;
}
// 获取“第一个节点”
static node* get_first_node()
{
return get_node(0);
}
// 获取“最后一个节点”
static node* get_last_node()
{
return get_node(count-1);
}
// 获取“双向链表中第index位置的元素”。成功,返回节点值;否则,返回-1。
void* dlink_get(int index)
{
node *pindex=get_node(index);
if (!pindex)
{
printf("%s failed!\n", __func__);
return NULL;
}
return pindex->p;
}
// 获取“双向链表中第1个元素的值”
void* dlink_get_first()
{
return dlink_get(0);
}
// 获取“双向链表中最后1个元素的值”
void* dlink_get_last()
{
return dlink_get(count-1);
}
// 将“pval”插入到index位置。成功,返回0;否则,返回-1。
int dlink_insert(int index, void* pval)
{
// 插入表头
if (index==0)
return dlink_insert_first(pval);
// 获取要插入的位置对应的节点
node *pindex=get_node(index);
if (!pindex)
return -1;
// 创建“节点”
node *pnode=create_node(pval);
if (!pnode)
return -1;
pnode->prev = pindex->prev;
pnode->next = pindex;
pindex->prev->next = pnode;
pindex->prev = pnode;
// 节点个数+1
count++;
return 0;
}
// 将“pval”插入到表头位置
int dlink_insert_first(void *pval)
{
node *pnode=create_node(pval);
if (!pnode)
return -1;
pnode->prev = phead;
pnode->next = phead->next;
phead->next->prev = pnode;
phead->next = pnode;
count++;
return 0;
}
// 将“pval”插入到末尾位置
int dlink_append_last(void *pval)
{
node *pnode=create_node(pval);
if (!pnode)
return -1;
pnode->next = phead;
pnode->prev = phead->prev;
phead->prev->next = pnode;
phead->prev = pnode;
count++;
return 0;
}
// 删除“双向链表中index位置的节点”。成功,返回0;否则,返回-1。
int dlink_delete(int index)
{
node *pindex=get_node(index);
if (!pindex)
{
printf("%s failed! the index in out of bound!\n", __func__);
return -1;
}
pindex->next->prev = pindex->prev;
pindex->prev->next = pindex->next;
free(pindex);
count--;
return 0;
}
// 删除第一个节点
int dlink_delete_first()
{
return dlink_delete(0);
}
// 删除组后一个节点
int dlink_delete_last()
{
return dlink_delete(count-1);
}
// 撤销“双向链表”。成功,返回0;否则,返回-1。
int destroy_dlink()
{
if (!phead)
{
printf("%s failed! dlink is null!\n", __func__);
return -1;
}
node *pnode=phead->next;
node *ptmp=NULL;
while(pnode != phead)
{
ptmp = pnode;
pnode = pnode->next;
free(ptmp);
}
free(phead);
phead = NULL;
count = 0;
return 0;
}
双向链表测试程序(dlink_test.c)
#include <stdio.h>
#include "double_link.h"
/**
* C 语言实现的双向链表的测试程序。
*
* (01) int_test()
* 演示向双向链表操作“int数据”。
* (02) string_test()
* 演示向双向链表操作“字符串数据”。
* (03) object_test()
* 演示向双向链表操作“对象”。
*
* @author skywang
* @date 2013/11/07
*/
// 双向链表操作int数据
void int_test()
{
int iarr[4] = {10, 20, 30, 40};
printf("\n----%s----\n", __func__);
create_dlink(); // 创建双向链表
dlink_insert(0, &iarr[0]); // 向双向链表的表头插入数据
dlink_insert(0, &iarr[1]); // 向双向链表的表头插入数据
dlink_insert(0, &iarr[2]); // 向双向链表的表头插入数据
printf("dlink_is_empty()=%d\n", dlink_is_empty()); // 双向链表是否为空
printf("dlink_size()=%d\n", dlink_size()); // 双向链表的大小
// 打印双向链表中的全部数据
int i;
int *p;
int sz = dlink_size();
for (i=0; i<sz; i++)
{
p = (int *)dlink_get(i);
printf("dlink_get(%d)=%d\n", i, *p);
}
destroy_dlink();
}
void string_test()
{
char* sarr[4] = {"ten", "twenty", "thirty", "forty"};
printf("\n----%s----\n", __func__);
create_dlink(); // 创建双向链表
dlink_insert(0, sarr[0]); // 向双向链表的表头插入数据
dlink_insert(0, sarr[1]); // 向双向链表的表头插入数据
dlink_insert(0, sarr[2]); // 向双向链表的表头插入数据
printf("dlink_is_empty()=%d\n", dlink_is_empty()); // 双向链表是否为空
printf("dlink_size()=%d\n", dlink_size()); // 双向链表的大小
// 打印双向链表中的全部数据
int i;
char *p;
int sz = dlink_size();
for (i=0; i<sz; i++)
{
p = (char *)dlink_get(i);
printf("dlink_get(%d)=%s\n", i, p);
}
destroy_dlink();
}
typedef struct tag_stu
{
int id;
char name[20];
}stu;
static stu arr_stu[] =
{
{10, "sky"},
{20, "jody"},
{30, "vic"},
{40, "dan"},
};
#define ARR_STU_SIZE ( (sizeof(arr_stu)) / (sizeof(arr_stu[0])) )
void object_test()
{
printf("\n----%s----\n", __func__);
create_dlink(); // 创建双向链表
dlink_insert(0, &arr_stu[0]); // 向双向链表的表头插入数据
dlink_insert(0, &arr_stu[1]); // 向双向链表的表头插入数据
dlink_insert(0, &arr_stu[2]); // 向双向链表的表头插入数据
printf("dlink_is_empty()=%d\n", dlink_is_empty()); // 双向链表是否为空
printf("dlink_size()=%d\n", dlink_size()); // 双向链表的大小
// 打印双向链表中的全部数据
int i;
int sz = dlink_size();
stu *p;
for (i=0; i<sz; i++)
{
p = (stu *)dlink_get(i);
printf("dlink_get(%d)=[%d, %s]\n", i, p->id, p->name);
}
destroy_dlink();
}
int main()
{
int_test(); // 演示向双向链表操作“int数据”。
string_test(); // 演示向双向链表操作“字符串数据”。
object_test(); // 演示向双向链表操作“对象”。
return 0;
}
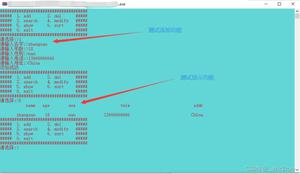
运行结果
----int_test----
dlink_is_empty()=0
dlink_size()=3
dlink_get(0)=30
dlink_get(1)=20
dlink_get(2)=10
----string_test----
dlink_is_empty()=0
dlink_size()=3
dlink_get(0)=thirty
dlink_get(1)=twenty
dlink_get(2)=ten
----object_test----
dlink_is_empty()=0
dlink_size()=3
dlink_get(0)=[30, vic]
dlink_get(1)=[20, jody]
dlink_get(2)=[10, sky]
2. C++实现双链表
实现代码
双向链表文件(DoubleLink.h)
#ifndef DOUBLE_LINK_HXX
#define DOUBLE_LINK_HXX
#include <iostream>
using namespace std;
template<class T>
struct DNode
{
public:
T value;
DNode *prev;
DNode *next;
public:
DNode() { }
DNode(T t, DNode *prev, DNode *next) {
this->value = t;
this->prev = prev;
this->next = next;
}
};
template<class T>
class DoubleLink
{
public:
DoubleLink();
~DoubleLink();
int size();
int is_empty();
T get(int index);
T get_first();
T get_last();
int insert(int index, T t);
int insert_first(T t);
int append_last(T t);
int del(int index);
int delete_first();
int delete_last();
private:
int count;
DNode<T> *phead;
private:
DNode<T> *get_node(int index);
};
template<class T>
DoubleLink<T>::DoubleLink() : count(0)
{
// 创建“表头”。注意:表头没有存储数据!
phead = new DNode<T>();
phead->prev = phead->next = phead;
// 设置链表计数为0
//count = 0;
}
// 析构函数
template<class T>
DoubleLink<T>::~DoubleLink()
{
// 删除所有的节点
DNode<T>* ptmp;
DNode<T>* pnode = phead->next;
while (pnode != phead)
{
ptmp = pnode;
pnode=pnode->next;
delete ptmp;
}
// 删除"表头"
delete phead;
phead = NULL;
}
// 返回节点数目
template<class T>
int DoubleLink<T>::size()
{
return count;
}
// 返回链表是否为空
template<class T>
int DoubleLink<T>::is_empty()
{
return count==0;
}
// 获取第index位置的节点
template<class T>
DNode<T>* DoubleLink<T>::get_node(int index)
{
// 判断参数有效性
if (index<0 || index>=count)
{
cout << "get node failed! the index in out of bound!" << endl;
return NULL;
}
// 正向查找
if (index <= count/2)
{
int i=0;
DNode<T>* pindex = phead->next;
while (i++ < index) {
pindex = pindex->next;
}
return pindex;
}
// 反向查找
int j=0;
int rindex = count - index -1;
DNode<T>* prindex = phead->prev;
while (j++ < rindex) {
prindex = prindex->prev;
}
return prindex;
}
// 获取第index位置的节点的值
template<class T>
T DoubleLink<T>::get(int index)
{
return get_node(index)->value;
}
// 获取第1个节点的值
template<class T>
T DoubleLink<T>::get_first()
{
return get_node(0)->value;
}
// 获取最后一个节点的值
template<class T>
T DoubleLink<T>::get_last()
{
return get_node(count-1)->value;
}
// 将节点插入到第index位置之前
template<class T>
int DoubleLink<T>::insert(int index, T t)
{
if (index == 0)
return insert_first(t);
DNode<T>* pindex = get_node(index);
DNode<T>* pnode = new DNode<T>(t, pindex->prev, pindex);
pindex->prev->next = pnode;
pindex->prev = pnode;
count++;
return 0;
}
// 将节点插入第一个节点处。
template<class T>
int DoubleLink<T>::insert_first(T t)
{
DNode<T>* pnode = new DNode<T>(t, phead, phead->next);
phead->next->prev = pnode;
phead->next = pnode;
count++;
return 0;
}
// 将节点追加到链表的末尾
template<class T>
int DoubleLink<T>::append_last(T t)
{
DNode<T>* pnode = new DNode<T>(t, phead->prev, phead);
phead->prev->next = pnode;
phead->prev = pnode;
count++;
return 0;
}
// 删除index位置的节点
template<class T>
int DoubleLink<T>::del(int index)
{
DNode<T>* pindex = get_node(index);
pindex->next->prev = pindex->prev;
pindex->prev->next = pindex->next;
delete pindex;
count--;
return 0;
}
// 删除第一个节点
template<class T>
int DoubleLink<T>::delete_first()
{
return del(0);
}
// 删除最后一个节点
template<class T>
int DoubleLink<T>::delete_last()
{
return del(count-1);
}
#endif
双向链表测试文件(DlinkTest.cpp)
#include <iostream>
#include "DoubleLink.h"
using namespace std;
// 双向链表操作int数据
void int_test()
{
int iarr[4] = {10, 20, 30, 40};
cout << "\n----int_test----" << endl;
// 创建双向链表
DoubleLink<int>* pdlink = new DoubleLink<int>();
pdlink->insert(0, 20); // 将 20 插入到第一个位置
pdlink->append_last(10); // 将 10 追加到链表末尾
pdlink->insert_first(30); // 将 30 插入到第一个位置
// 双向链表是否为空
cout << "is_empty()=" << pdlink->is_empty() <<endl;
// 双向链表的大小
cout << "size()=" << pdlink->size() <<endl;
// 打印双向链表中的全部数据
int sz = pdlink->size();
for (int i=0; i<sz; i++)
cout << "pdlink("<<i<<")=" << pdlink->get(i) <<endl;
}
void string_test()
{
string sarr[4] = {"ten", "twenty", "thirty", "forty"};
cout << "\n----string_test----" << endl;
// 创建双向链表
DoubleLink<string>* pdlink = new DoubleLink<string>();
pdlink->insert(0, sarr[1]); // 将 sarr中第2个元素 插入到第一个位置
pdlink->append_last(sarr[0]); // 将 sarr中第1个元素 追加到链表末尾
pdlink->insert_first(sarr[2]); // 将 sarr中第3个元素 插入到第一个位置
// 双向链表是否为空
cout << "is_empty()=" << pdlink->is_empty() <<endl;
// 双向链表的大小
cout << "size()=" << pdlink->size() <<endl;
// 打印双向链表中的全部数据
int sz = pdlink->size();
for (int i=0; i<sz; i++)
cout << "pdlink("<<i<<")=" << pdlink->get(i) <<endl;
}
struct stu
{
int id;
char name[20];
};
static stu arr_stu[] =
{
{10, "sky"},
{20, "jody"},
{30, "vic"},
{40, "dan"},
};
#define ARR_STU_SIZE ( (sizeof(arr_stu)) / (sizeof(arr_stu[0])) )
void object_test()
{
cout << "\n----object_test----" << endl;
// 创建双向链表
DoubleLink<stu>* pdlink = new DoubleLink<stu>();
pdlink->insert(0, arr_stu[1]); // 将 arr_stu中第2个元素 插入到第一个位置
pdlink->append_last(arr_stu[0]); // 将 arr_stu中第1个元素 追加到链表末尾
pdlink->insert_first(arr_stu[2]); // 将 arr_stu中第3个元素 插入到第一个位置
// 双向链表是否为空
cout << "is_empty()=" << pdlink->is_empty() <<endl;
// 双向链表的大小
cout << "size()=" << pdlink->size() <<endl;
// 打印双向链表中的全部数据
int sz = pdlink->size();
struct stu p;
for (int i=0; i<sz; i++)
{
p = pdlink->get(i);
cout << "pdlink("<<i<<")=[" << p.id << ", " << p.name <<"]" <<endl;
}
}
int main()
{
int_test(); // 演示向双向链表操作“int数据”。
string_test(); // 演示向双向链表操作“字符串数据”。
object_test(); // 演示向双向链表操作“对象”。
return 0;
}
示例说明
在上面的示例中,我将双向链表的"声明"和"实现"都放在头文件中。而编程规范告诫我们:将类的声明和实现分离,在头文件(.h文件或.hpp)中尽量只包含声明,而在实现文件(.cpp文件)中负责实现!
那么为什么要这么做呢?这是因为,在双向链表的实现中,采用了模板;而C++编译器不支持对模板的分离式编译!简单点说,如果在DoubleLink.h中声明,而在DoubleLink.cpp中进行实现的话;当我们在其他类中创建DoubleLink的对象时,会编译出错。具体原因,可以参考"为什么C++编译器不能支持对模板的分离式编译"。
运行结果
----int_test----
is_empty()=0
size()=3
pdlink(0)=30
pdlink(1)=20
pdlink(2)=10
----string_test----
is_empty()=0
size()=3
pdlink(0)=thirty
pdlink(1)=twenty
pdlink(2)=ten
----object_test----
is_empty()=0
size()=3
pdlink(0)=[30, vic]
pdlink(1)=[20, jody]
pdlink(2)=[10, sky]
3. Java实现双链表
实现代码
双链表类(DoubleLink.java)
/**
* Java 实现的双向链表。
* 注:java自带的集合包中有实现双向链表,路径是:java.util.LinkedList
*
* @author skywang
* @date 2013/11/07
*/
public class DoubleLink<T> {
// 表头
private DNode<T> mHead;
// 节点个数
private int mCount;
// 双向链表“节点”对应的结构体
private class DNode<T> {
public DNode prev;
public DNode next;
public T value;
public DNode(T value, DNode prev, DNode next) {
this.value = value;
this.prev = prev;
this.next = next;
}
}
// 构造函数
public DoubleLink() {
// 创建“表头”。注意:表头没有存储数据!
mHead = new DNode<T>(null, null, null);
mHead.prev = mHead.next = mHead;
// 初始化“节点个数”为0
mCount = 0;
}
// 返回节点数目
public int size() {
return mCount;
}
// 返回链表是否为空
public boolean isEmpty() {
return mCount==0;
}
// 获取第index位置的节点
private DNode<T> getNode(int index) {
if (index<0 || index>=mCount)
throw new IndexOutOfBoundsException();
// 正向查找
if (index <= mCount/2) {
DNode<T> node = mHead.next;
for (int i=0; i<index; i++)
node = node.next;
return node;
}
// 反向查找
DNode<T> rnode = mHead.prev;
int rindex = mCount - index -1;
for (int j=0; j<rindex; j++)
rnode = rnode.prev;
return rnode;
}
// 获取第index位置的节点的值
public T get(int index) {
return getNode(index).value;
}
// 获取第1个节点的值
public T getFirst() {
return getNode(0).value;
}
// 获取最后一个节点的值
public T getLast() {
return getNode(mCount-1).value;
}
// 将节点插入到第index位置之前
public void insert(int index, T t) {
if (index==0) {
DNode<T> node = new DNode<T>(t, mHead, mHead.next);
mHead.next.prev = node;
mHead.next = node;
mCount++;
return ;
}
DNode<T> inode = getNode(index);
DNode<T> tnode = new DNode<T>(t, inode.prev, inode);
inode.prev.next = tnode;
inode.next = tnode;
mCount++;
return ;
}
// 将节点插入第一个节点处。
public void insertFirst(T t) {
insert(0, t);
}
// 将节点追加到链表的末尾
public void appendLast(T t) {
DNode<T> node = new DNode<T>(t, mHead.prev, mHead);
mHead.prev.next = node;
mHead.prev = node;
mCount++;
}
// 删除index位置的节点
public void del(int index) {
DNode<T> inode = getNode(index);
inode.prev.next = inode.next;
inode.next.prev = inode.prev;
inode = null;
mCount--;
}
// 删除第一个节点
public void deleteFirst() {
del(0);
}
// 删除最后一个节点
public void deleteLast() {
del(mCount-1);
}
}
测试程序(DlinkTest.java)
/**
* Java 实现的双向链表。
* 注:java自带的集合包中有实现双向链表,路径是:java.util.LinkedList
*
* @author skywang
* @date 2013/11/07
*/
public class DlinkTest {
// 双向链表操作int数据
private static void int_test() {
int[] iarr = {10, 20, 30, 40};
System.out.println("\n----int_test----");
// 创建双向链表
DoubleLink<Integer> dlink = new DoubleLink<Integer>();
dlink.insert(0, 20); // 将 20 插入到第一个位置
dlink.appendLast(10); // 将 10 追加到链表末尾
dlink.insertFirst(30); // 将 30 插入到第一个位置
// 双向链表是否为空
System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
// 双向链表的大小
System.out.printf("size()=%d\n", dlink.size());
// 打印出全部的节点
for (int i=0; i<dlink.size(); i++)
System.out.println("dlink("+i+")="+ dlink.get(i));
}
private static void string_test() {
String[] sarr = {"ten", "twenty", "thirty", "forty"};
System.out.println("\n----string_test----");
// 创建双向链表
DoubleLink<String> dlink = new DoubleLink<String>();
dlink.insert(0, sarr[1]); // 将 sarr中第2个元素 插入到第一个位置
dlink.appendLast(sarr[0]); // 将 sarr中第1个元素 追加到链表末尾
dlink.insertFirst(sarr[2]); // 将 sarr中第3个元素 插入到第一个位置
// 双向链表是否为空
System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
// 双向链表的大小
System.out.printf("size()=%d\n", dlink.size());
// 打印出全部的节点
for (int i=0; i<dlink.size(); i++)
System.out.println("dlink("+i+")="+ dlink.get(i));
}
// 内部类
private static class Student {
private int id;
private String name;
public Student(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "["+id+", "+name+"]";
}
}
private static Student[] students = new Student[]{
new Student(10, "sky"),
new Student(20, "jody"),
new Student(30, "vic"),
new Student(40, "dan"),
};
private static void object_test() {
System.out.println("\n----object_test----");
// 创建双向链表
DoubleLink<Student> dlink = new DoubleLink<Student>();
dlink.insert(0, students[1]); // 将 students中第2个元素 插入到第一个位置
dlink.appendLast(students[0]); // 将 students中第1个元素 追加到链表末尾
dlink.insertFirst(students[2]); // 将 students中第3个元素 插入到第一个位置
// 双向链表是否为空
System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
// 双向链表的大小
System.out.printf("size()=%d\n", dlink.size());
// 打印出全部的节点
for (int i=0; i<dlink.size(); i++) {
System.out.println("dlink("+i+")="+ dlink.get(i));
}
}
public static void main(String[] args) {
int_test(); // 演示向双向链表操作“int数据”。
string_test(); // 演示向双向链表操作“字符串数据”。
object_test(); // 演示向双向链表操作“对象”。
}
}
运行结果
----int_test----
isEmpty()=false
size()=3
dlink(0)=30
dlink(1)=20
dlink(2)=10
----string_test----
isEmpty()=false
size()=3
dlink(0)=thirty
dlink(1)=twenty
dlink(2)=ten
----object_test----
isEmpty()=false
size()=3
dlink(0)=[30, vic]
dlink(1)=[20, jody]
dlink(2)=[10, sky]
以上就是本文的全部内容,希望大家能够理解,对大家有所帮助。
以上是 简单介绍线性表以及如何实现双链表 的全部内容, 来源链接: utcz.com/p/208826.html