padding oracle 原理深度解析 & CBC 字节翻转攻击原理解析
作者:天融信阿尔法实验室
公众号:https://mp.weixin.qq.com/s/OtGw-rALwpBkERfvqdZ4kQ
1、padding oracle 简介
首先我们先看一下padding oracle漏洞简单描述,以下是来自百度百科的解释
Padding的含义是“填充”,在解密时,如果算法发现解密后得到的结果,它的填充方式不符合规则,那么表示输入数据有问题,对于解密的类库来说,往往便会抛出一个异常,提示Padding不正确。Oracle在这里便是“提示”的意思,一开始看到漏洞名称中有oracle的时候我也被误导了,单实际上和甲骨文公司没有任何关系。
2、常见的加密模式
首先我们知道,加密的方法有很多种,分为两大类 对称加密和非对称加密,
对称加密又称单密钥加密,也就是字面意思,加密解密用的都是同一个密钥,常见的对称加密算法,例如DES,3DES和AES等
非对称加密,就是说密钥分两个,一个公钥,一个私钥,加解密过程就是公钥加密私钥解密和私钥加密公钥匙解密,常见的非对称加密算法有,RSA DSA等
初次接触这个漏洞的人,多会认为此漏洞是一个加密算法的漏洞,然而实际却并非如此随着讲解就会明白真正的漏洞点出在何处
我们常用的加密可以分为两部分来理解,一部分是加密算法,这部分的话过于高深需要相当程度的密码学知识做基础。而另一部分,就是加密模式,这部分相较于加密算法来说就简单太多了,而此次出现padding oracle漏洞的就是CBC加密模式
这里我从网上截几个图解释下这个CBC模式是个什么东西,出了这个CBC模式外还有哪些个加密模式。
AES是对称加密,对称加密呢有两大类加密模式,即分组加密和流加密,AES分组加密有五种加密模式:
电码本模式(Electronic Codebook Book (ECB));
密码分组链接模式(Cipher Block Chaining (CBC));
计算器模式(Counter (CTR));
密码反馈模式(Cipher FeedBack (CFB));
输出反馈模式(Output FeedBack (OFB))。
此次出现问题的是CBC加密模式,为了方便理解加密模式 我们就顺便也讲一下ECB加密模式。
3、ECB加密模式简介
首先我们要明白加密算法和加密模式是两个概念,AES是加密算法,加密算法是通过接收方和发送方协商产生密钥,结合一系列的各种位运算之后得出的结果。而加密模式是在加密算法的基础上,把加密的方式变得更加复杂一点,首先我们看下最简单直接的ECB加密模式

可以看到ECB加密模式的思想非常直白,就是把明文分为等长的块,然后一块一块的加密,最后再把每一块加密后的密文拼接在一起。这就是ECB加密模式
4、CBC加密模式简介
接下来就讲一讲这次的重点,也就是CBC加密模式

首先多了一个IV,这个IV我们一般称作初始向量,首先明文还是那个明文,分块还是要分块,在通过AES加密之前我们需要先将明文块0,也就是第一块明文,和我们的初始向量IV做异或操作,这个初始向量IV是随机的,而且长度是和我们的每一块明文块等长,因为要按位进行异或嘛。这样无疑就在加密之前就已经先行打乱的我们的明文,与初始化向量异或后的明文,我们暂且称它为中间值,我们此时再对这个中间值进行AES加密,这样第一块明文的加密就完成了。
从上面哪个截图我们不难看的出,CBC模式是一个链式结构,这个链接的关键点就在于,我们加密第二块明文的时候同样也需要一个初始化向量来和我们第二块明文也就是明文块1来进行异或,那这个初始话向量哪来的呢,总不可能系统为每一块明文都分配一个随机的初始化向量吧,这样成本过高。所以我们将第一块明文加密后的密文,作为第二个明文加密时的初始化向量,而这个就是这个链式结构的连接点,后续的步骤就是不断重复加密第一块明文时所做的操作,直至最后一块明文加密完成。
感觉上CBC模式比ECB模式流程上复杂这么多,应该比ECB模式更安全才对,理论上讲确实,因为引入了初始化向量这个一个操作,所以CBC加密的结果随机性更高,相同的明文ECB加密每一次的结果都是相同的,也就是明文和密文一对一。 而CBC由于多了一个随机的初始化向量,所以同样的明文CBC每一次加密出来的结果都是不一样的。由此来看CBC明显比ECB更安全,但是CBC这个模式在设计上存在缺陷 ,而这个缺陷就导致了著名的padding oracle攻击
既然有加密,那肯定就会有解密,而且此次被攻击的是服务端,那肯定就是我们客户端发送加密数据,然后服务端解密我们的数据,然后给我们反馈,要么解密成功要么解密不成功,而攻击就发生在服务端解密和反馈这个过程。
不知道讲解到此处大家心里有没有一个疑惑。
回过头来看一下,前文说了分组加密的分组要怎么样?等长对不对 而且 初始化向量和每一组分组都要等长对不对?
用AES和DES两个加密算法来举例子 AES的分组长度为每块16字节,DES呢则是每块8字节,那么怎么能保证我们的明文长度是16或者8的整数倍呢?
当然没办法保证,所以我们就要采取措施强制让明文为16或者8的整数倍,最直接的方法自然就是直接填充,不够就补到它够为止。这也就是所谓的padding 填充。
5、padding oracle 原理
而CBC加密模式的设计者自然也考虑到了这问题,剩余的几位当然不能随便填充,而要填充一些有价值的数值。
假如说此时我们按8字节为一个明文分组,分到最后发现最后一组缺了一个字节,程序不会填一些随机数,亦或者将不够的位数全填零。CBC模式最后的填充方法,就是缺了一位就填一个0x01,缺了两位就填两个0x02,缺了三位就填三个0x03,以此往后类推缺n个就填n个0x0n。哪怕当明文正好时分组的整数倍时,也会填充8个0x08,即使是整数倍也要填充。这样就导致了无论我们明文的长度是多少,我们CBC模式加密是都会在明文的最后进行填充,以确保分段的长度是8的整数倍。
不理解的可以看一下具体的填充算法
add = length - (count % length)plaintext = plaintext + ('\0' * add) #填充
通过下图可以更好的让我们理解这种填充的思想
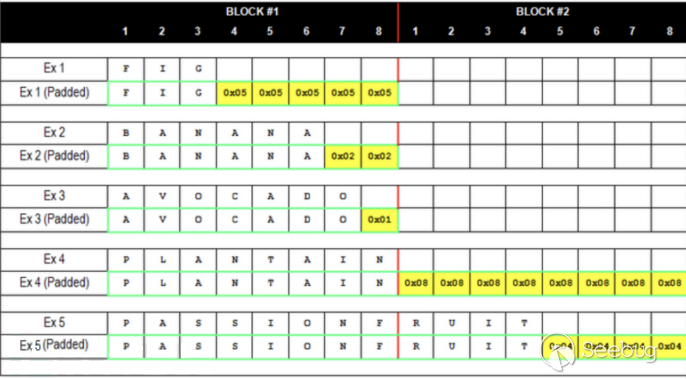
之所以选择这么填充,就肯定是有它的道理的。
前文说了,有加密就有解密,那解密的时候这个填充位就会起到很大的作用,CBC模式解密的流程其实就是加密流程再反过来。
我们再看一下加密的流程
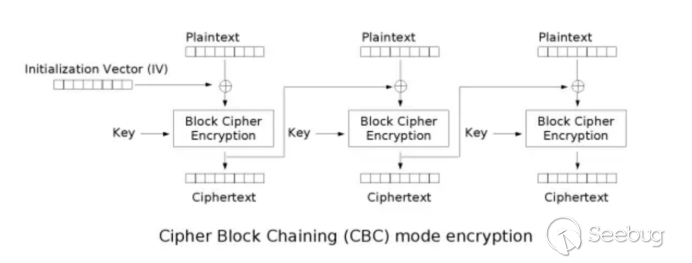
下面是解密的流程

此时我们先思考一个问题就是我们平常是通过什么来判断一个业务逻辑或者是功能点是存在漏洞的?那就是通过服务端的回显来判断对不对?如果说服务端给我们的回复一直都是一样的我们能判断这个功能点就是存在漏洞么?举个例子拿暴力破解这个漏洞来说,通常都是用在攻击网站的登陆点上,通常存在暴力破解漏洞的登陆点都会返回这样的信息“该用户名不存在”,“密码输入错误”。通过这两条返回信息我们可以判断用户名是否存在和密码是否输入正确。判断的依据就是返回信息的不同,正是因为用户名错误和密码错误的返回消息的差异导致了我们可以去判断我们输入究竟是用户名有错还是密码有错。
而padding oracle攻击,同样是通过服务端返回的信息的差异而产生的,在这里我要先提一下解密时的一个步骤,同样也是我们padding oracle的核心利用点。
之前加密的时候我们就知道了,为了保证分组加密时每一组都能保证等长,我们在加密时需要对最后一组不等长的情况进行填充,缺n位就填n个0x0n。此时解密的时候这些个填充位就派上用场了,我们在解密步骤时,按照顺序,首先是密文第一组,会先被解密掉,揭秘出来的结果呢就是我们的初始向量IV和第一段明文异或的结果也就是我们之前说的中间值。此时我们将中间值和初始向量IV进行异或,得到的就是我们第一组的明文,然后以此类推知道解密完最后一组密文后。此时此刻,按理说程序会将解密好的数据交由业务代码来进行后续的判断,比如验证揭秘后的用户名密码是否匹配。或者用于校验用户身份的Cookie值是否正确。
理论是如此但是实际上这中间还有一个步骤就是,程序要判断明文最后的填充位是否正确。
这个判断本身是没问题的,可以直接排除掉一些错误的加密数据,和被人恶意篡改的数据。但是一旦判断出明文最后的填充位是错误的,返回给客户端的信息,给攻击者提供攻击思路。
首先如果密文解密成明文后,填充位判断正确,而且经过业务逻辑代码的校验后,也是正确,那么服务端会返回200的状态码。
如果密文解密成明文后,填充位判断正确,但是业务逻辑判断不通过,也就是说这个明文有问题,纳闷服务端会返回200或者300等状态码。
最后如果密文解密成明文后,填充位判断不正确,就会返回500等状态码。
不知道大家有没有发现一个问题就是,填充位的正确与否,服务端返回的状态码是不一样的!!
Padding orlace正是通过这一点的不同来做文章的
那么如何进行padding 我们首先就从一个简单的例子开始讲起,也是很多大佬都用的例子。
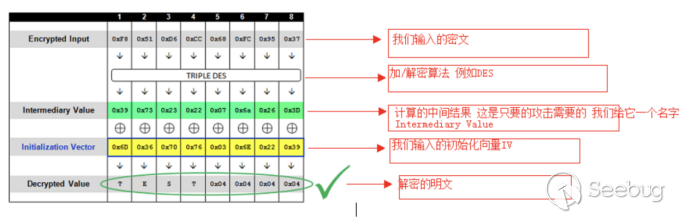
首先,以加密解密“TEST”这个字符串为例,“TEST”字符串总共占四个字符串,如果按8字节进行分组,那么很明显是不够的,所以我们需要补充4个0x04
然后由程序进行加密,得出加密的结果是”F851D6CC68FC9537”每两位16进制是一个字节,此时我们审视一下我们当前的已知条件
我们此时不是知道明文是什么,但是我们知道密文是“F851D6CC68FC9537”
同时我们还知道一个条件那就是该密文的初始化向量,没错,如果要进行padding oracle这个攻击的话,已知初始化向量是一个必须的条件。
同时我们可以和服务端进行交互,这个交互是指我们发送加密数据到服务端,服务端回判断我们发送的密文解密后填充位是否正确,并返回给我们填充位正确的状态码,或者填充位不正确的状态码。
刚才的已知条件中,我提到了初始化向量必须已知才能进行攻击,那么这个初始化向量在哪呢?
一般是在密文的头部
我们可以看到图中初始化向量的值是“6D367076036E2239”
举个例子,比如我们使用加密传输了一个值,值的名字叫padding
Padding= 6D367076036E2239F851D6CC68FC9537
我们可以看到“6D367076036E2239”放在密文的前面,又已知初始化向量和密文的分组等长所以,分组长度为8字节,那么初始化向量的长度自然也是8字节,由此我们就可以明确前八个字节是初始化向量,
理论上讲,“F851D6CC68FC9537”这段密文我们如果知道密钥的话,就可以直接解开这段密文得出他的明文,但是很明显我们不知道,如果知道密钥了那我们还折腾个啥
那么接下来的操作就是利用我们手上已有的条件,在不知道密钥的情况下得到这段密文的明文
首先根据解密步骤
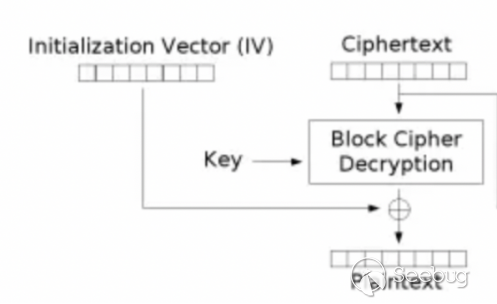
服务端收到密文的时候回先对密文进行解密,也就是对“F851D6CC68FC9537”
这段密文进行解密,的到我们的中间值,注意此时中间值是多少我们并不知道,因为服务端不可能把中间值返回给我们。
然后通过中间值和初始化向量异或我们就可以得到“F851D6CC68FC9537”的明文
初始化向量我们是已知的也就是“6D367076036E2239”也就是说我们离得到明文就差一个中间值,如果我们知道中间值是多少,那我们直接异或运算一下就可以得出明文了,关键就在于怎么得到这个中间值?
还记得之前说的程序回判断填充位并返回不同的状态么?
此时我们将初始化向量全部制为零,此时发送给服务端的数据就变成了
padding=0000000000000000F851D6CC68FC9537然后看图

还是一样的步骤,程序解密密文得到中间值,然后和初始化向量异或得到明文,然后程序再判断填充位是否正确。
我们知道0和数异或的结果都是该数本身
所以中间值和0异或的结果还是中间值本身,我们可以从图中看到异或的结果是3D,此时我们是不可能知道这个异或出来的结果是3D的,但是此时服务端会报一个错,那就是填充位错误,为什么会报这个错,因为之前说了,填充文在8个字节为分组的情况下,最多只可能填到8个0x08,所以怎么可能会有0x3D呢?
那怎么样才能不报这个错呢?以最后一位为例
如果此时异或出来的结果为 “39732322076a2601”也就是异或出来的结果最后一位为0x01时就不会报填充位错误了。但是后续还会在爆一个错误,那就是业务判断你这个解密出来的明文数据也就是“39732322076a2601”不正确,因为我们初始化向量都制为零的,所以这个明文当然是错误的,不过这都不重要。
此时我们知道了,当最终解除出来的明文的最后一位位0x01时,我们的程序就不会报填充位错误,那一次类推如果解出来为“39732322076a0202”“ 3973232207030303”…… “ 0808080808080808”时也不会报填充位错误。
所以我们从假如最后一位为0x01开始,由于中间是是固定不变的,我们就需要变化初始化向量的最后一个字节让其和中间值的最后一个字节异或的结果为0x01, 所以此时我们需要用到穷举的方法,一个字节的范围为,0x00-0xFF,最多也就是需要尝试256次,

此时我们根据上图可以看出,当最后一位异或结果为0x01时,我们此时的初始化向量为
‘’0000000000000066‘’ 又已知0x01是中间值和初始化向量异或得出的结果,所以我们将此时我们用来爆破的初始化向量的最后一位,也就是“0x66”与0x01向异或,就可以得出真正的中间值的最后一个字节,也就是0x67。
以此类推,直到异或结果为“0808080808080808”,我们多需要尝试的次数,最多也不过256*8次也就是2048次,这样我们就可以绕过加密,从而直接获得密文的明文。
6、CBC字节翻转攻击
以上的手段可以让我们绕过加解密从而直接获得明文,不知道大家有没有发现一个问题,来我们再次观察一下解密过程
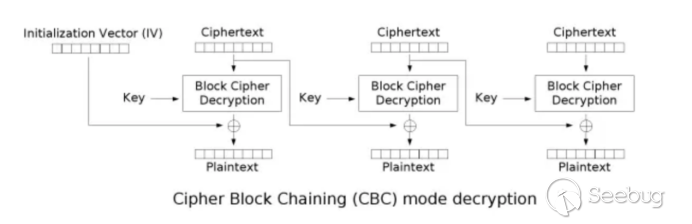
解密的第一步,首先用后台用密钥,将密文解密然后将解密得出的中间值与初始化向量IV做异或操作,得到第一段密文的明文。
解密的第二步,首先用后台用密钥,将密文解密然后将解密得出的中间值与上一段密文做异或操作,得到第二段密文的明文。
不难看出,下一段明文的内容是受到上一段密文的影响的,那么是否存在我们通过修改前一段密文或者初始化向量来达到修改下一段密文的明文的效果
打个比方说我们明文是“admin”然后加密传输到后端,后端解密出来的结果是“bdmin”
可不可以实现呢?当然是可以的
首先我们再理一下这个过程,“admin”首先和初始化向量异或得到一个8字节的密文,然后由于按照8字节来划分,所以初始化向量自然也是8字节,为了方便传递给后台识别,初始化向量转化成8字节大小的十六进制数放在加密好的密文开头,然后发送给后台。
后台受到密文后,将前八字节的十六进制出提取出来作为初始化向量,然后将剩下的密文,使用密钥解密后然后和初始化向量做异或操作,得出最终的明文。
问题还是出在了解密过程中的异或操作,这个初始化向量是我们可控的
我们想要的结果就是密文和我们修改过后的初始化向量
此时我们要清楚一个基本的异或运算
我们使用“qwerasdf”来作为我们的初始化向量 “admin”作为要加密传输的明文,也就是说我们首先进行异或操作时是有“q”和“a”来进行异或的
所以有“q” xor “a” 来作为第一步,这个异或的结果会在后台用密钥解密出来后再与初始化向量“q”来异或得出明文“a”
所以此时有“q” xor “a” xor “q” == “a”这么一个式子
我们将“q” xor “a”的结果设为X
既X = “q” xor “a”
,X就是作为中间值被加密然后传到后台的
此时我们将X 作为参数再与我们的目标值“b”进行一次异或
也就是说 X xor “b” 这个结果我们设为Y
此时得到Y == X xor “b”
再根据上一个式子可以得到,Y = “q” xor "a" xor " b"
已知X是未经修改的IV与明文异或的结果也就是所谓的中间值,也就说解密时X时作为解密时的中间值同样要参与到解密时的异或步骤,但是如果我们在传递数据时将“q”更改为我们的Y。让Y去和X进行异或操作,最终得到的结果就变成了”b“ ,这样我们就实现了更改明文的第一个字节,接下来的同样是进行重复操作。
这就是所谓的CBC字节翻转攻击的原理,下面贴出实现代码。
from pyDes import des, CBC, PAD_PKCS5import binascii
# 秘钥
KEY = 'mHAxsLYz'
#初始化向量
KEY2 = "qwerasdf"
def des_encrypt(s):
"""
DES 加密
:param s: 原始字符串
:return: 加密后字符串,16进制
"""
secret_key = KEY
iv = KEY2
k = des(secret_key, CBC, iv, pad=None, padmode=PAD_PKCS5)
en = k.encrypt(s, padmode=PAD_PKCS5)
return binascii.b2a_hex(en)
def des_descrypt(s,iv):
"""
DES 解密
:param s: 加密后的字符串,16进制
:return: 解密后的字符串
"""
secret_key = KEY
iv = iv
k = des(secret_key, CBC, iv, pad=None, padmode=PAD_PKCS5)
de = k.decrypt(binascii.a2b_hex(s), padmode=PAD_PKCS5)
return de
str = des_encrypt("admin")
cipher = bytes(KEY2,encoding='utf-8')
print(cipher)
x = bytes([ord(chr(cipher[0]))^ord('a')^ord('b')])+cipher[1:]
x2 = cipher[0]
print(x)
str3 = des_descrypt(str,x)
print(str3)
下面是执行结果

以上是 padding oracle 原理深度解析 & CBC 字节翻转攻击原理解析 的全部内容, 来源链接: utcz.com/p/199517.html