有一个x*y网络，小团在此网格上从左上角走到右下角，只能走格点且只能往右走或往下走

  • Z时代
  • 2024-01-10
  • 分类：IT

计算有多少种走法。给定正整数int x,int y,请返回小团的走法数目
输入一行，逗号隔开的正整数x,y取值范围〔1，10〕
输出包括一行，为走法数目

function main(parm_1,param_2,param_n){
    if(parm_1=parm_2){
        param_n = parm_1 = 1 ?2 :2+4^(parm_1-1);
    }
    if(parm_1=parm_2>1){
        param_n = 2+;
    }
    if(parm_1>parm_2){
        param_n = ;
    }
    if(parm_1<parm_2){
        param_n = ;
    }
    return param_n;
}

回答：

看下面的图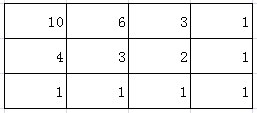
图片描述

计算过程：

  1. 把底边和右边的每个格子标记为1

  2. 其余格子从右下角往右上角依次遍历

  3. 每个格子的值是其右边和下边格子值的和

  4. 遍历到右上角后求得最终结果

例如上图的结果为10。

这种解法依据的思路，由于每个格子只能向右或向下走，那么它的走法就由其右边格子的走法和下边格子的走法之和。而最下边和最右边的每个格子都只有唯一的走法。由此就能推导出其余格子的走法。

PS：这种方法需要遍历一遍，复杂度为O(n)。除了这种方法之外，也许还可以从数学的角度来找到通项公式，从而一次求得最终结果也说不定。

回答：

function get(x, y){return x*y==0?1:(get(x,y-1)+get(x-1,y));}

其实就是组合数C(x+y,x)，楼上那个走网格对应的就是get(3,2)

以上是 有一个x*y网络，小团在此网格上从左上角走到右下角，只能走格点且只能往右走或往下走 的全部内容， 来源链接： utcz.com/p/179702.html

回到顶部