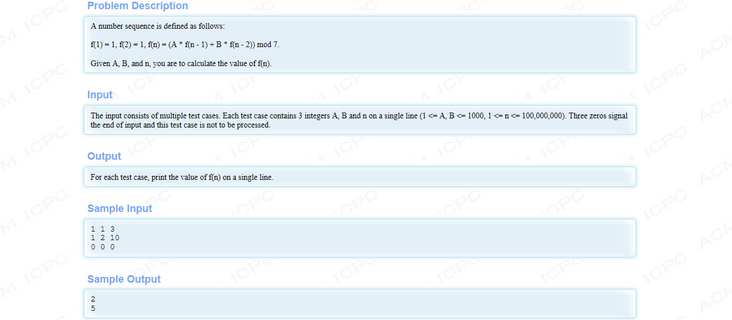
一道简答的算法

• Z时代
• 2024-01-10
• 分类：IT

1. 列表项目

     public static void main(String[] args) {
         Scanner in=new Scanner(System.in);
         while(in.hasNext()){
            int A=in.nextInt();
            int B=in.nextInt();
            int n=in.nextInt();
            if(A>=1 && A<=1000 && B>=1 && B<=1000 && n>=1 && n<=100000000){
            if(A==0 && B==0 && n==0){
                break;
            }
            int a[]=new int[n];
            if(n==1){
                a[0]=1;
            }
            if(n==2){
                a[0]=1;
                a[1]=1;
            }
            if(n>2){
                a[0]=1;
                a[1]=1;
            for(int i=2;i<n;i++){
                a[i]=(A * a[i-1] + B * a[i-2])%7;
            }
            }
            System.out.println(a[n-1]);
         }
        }
    }

我这样写，显示错误。

不知道哪里错了。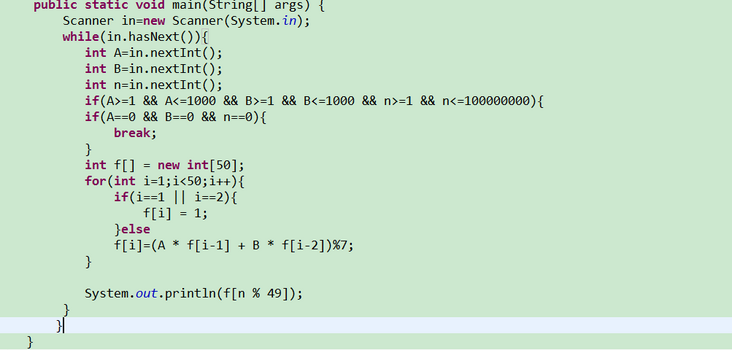

我这样写对的，不知道上一种方法哪里错了

回答：

报啥错你看了么？显示错误这样的问题描述，如果是问你自己，你该如何回答？

推测是OOM了 ，算法没啥问题，但是如果n=100000000，就要分将近400M内存给new int[n];

一般的ACM平台，不会给这么大内存吧

回答：

这题就是斐波那契的变种，三种方法可以得出结果，第一种是传统的递归模式（效率极低，请勿使用），第二种是尾递归，第三种是单次循环，都可以使用。

javaimport java.util.Scanner;
public class Main {
    private int A,B;
    Main(int A,int B){
        this.A=A;
        this.B=B;
    }
    // 递归，效率极低
    public int answer(int n){
        if(n==1 || n==2)return 1;
        return (A*answer(n-1)+B*answer(n-2))%7;
    }
    // 尾递归，效率高
    public int answer2(int n){
        return answer2(n,1,1);
    }
    public int answer2(int n,int x,int y) {
        if(n==1 || n==2)return y;
        return answer2(n-1,y,(A*y+B*x)%7);
    }
    // 单次循环，效率高
    public int answer3(int n){
        if(n==1 || n==2)return 1;
        int x=1,y=1;
        for(int i=3;i<=n;i++){
            int z=y;
            y=(A*y+B*x)%7;
            x=z;
        }
        return y;
    }
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
        while(in.hasNext()){
            int A=in.nextInt(),B=in.nextInt(),n=in.nextInt();
            if(A==0 && B==0 && n==0){
                break;
            }
            if(A>=1 && A<=1000 && B>=1 && B<=1000 && n>=1 && n<=100000000){
                System.out.println(new Main(A,B).answer3(n));
            }
        }
    }
}

以上是 一道简答的算法 的全部内容， 来源链接： utcz.com/p/173426.html