3.4 autograd与逻辑回归

                                                                                       点击此处返回总目录

一、自动求导系统

二、逻辑回归实现

一、autograd -- 自动求导系统

我们知道深度学习模型的训练就是不断地更新权值。而权值的更新需要求解梯度。因此，梯度在模型训练中是至关重要的。

然而求解梯度是十分繁琐的。因此pytorch提供自动求导系统。

我们不需要手工计算梯度，只需要搭建好前向传播的计算图，然后根据pytorch中的autograd就可以得到所有张量的梯度。

现在我们来学习一下autograd中的方法。

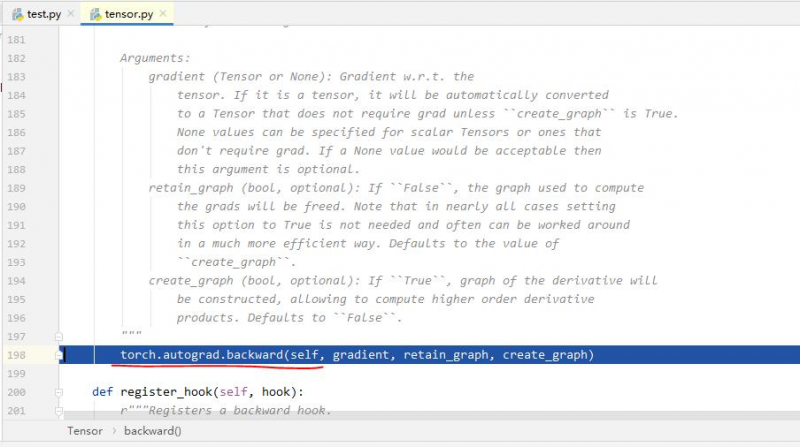
1. torch.autograd.backward(tensors, grad_tersors=None, retain_graph=None, create_graph=False)

自动求取梯度。

tensors                         #用于求导的张量，如loss

grad_tersors                 #多梯度权重。当有多个loss要计算梯度的时候，就要通过这个来设置权重。【例3】

retain_graph                 #保存计算图。由于pytorch是动态图。当运行了一次反向传播之后，计算图就会被释放掉。

                                      【例1】【例2】

create_graph=False     #创建导数计算图，用于高阶求导

在《计算图与动态图机制》里讲过，调用y.backward()，就可以计算得到各个张量的梯度。

那么y.backward() 与torch.autograd.backward()有什么关系呢？

通过在y.backward()前加断点，调试，进入可以发现：

y.backward()就是调用了torch.autograd.backward()函数。

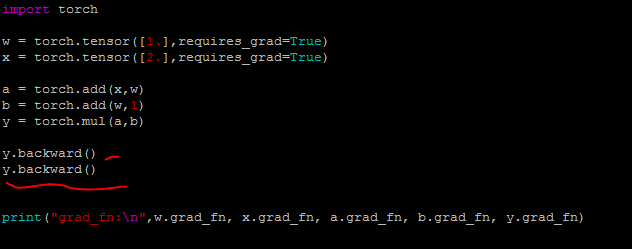
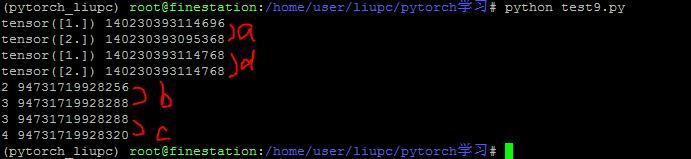
例1：如果执行两次y.backward()则会报错

结果：

报错原因就是执行一次反向传播后，计算图被释放了。它也说了只要把backward()的retain_graph属性设置为True，就可以了。

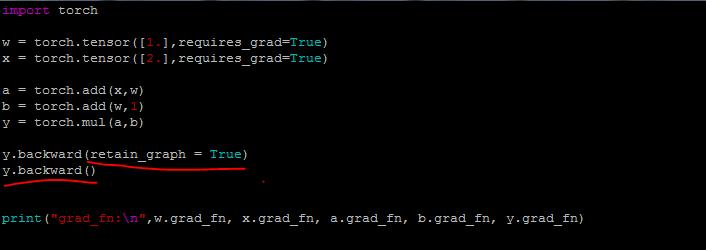
例2：把backward()的retain_graph属性设置为True，就可以不释放计算图了。这样就可以再次使用计算图了。

结果：

例3：（以后用到再补充）

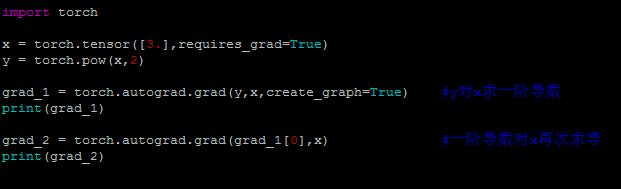
2. torch.autograd.grad(outputs, inputs, grad_outputs=None, retain_graph=None,create_graph=False )

用于求取梯度，函数返回的是想要的那一个张量的梯度。

outputs                         #用于求导的张量，如loss

inputs                           #需要求梯度的张量。

grad_tersors                 #多梯度权重。当有多个loss要计算梯度的时候，就要通过这个来设置权重。

retain_graph                 #保存计算图。由于pytorch是动态图。

create_graph=False     #创建导数计算图，用于高阶求导。【例1】

例1：

结果：

总结：

pytorch的自动求导系统中有三个需要注意到地方。

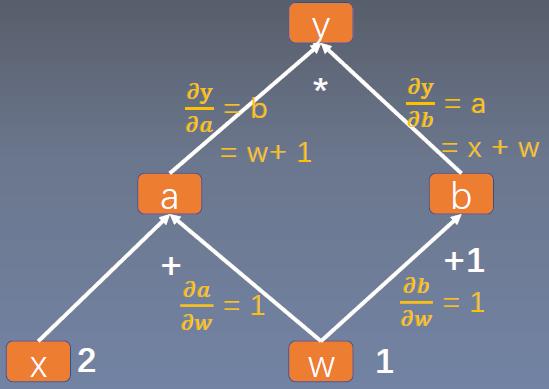
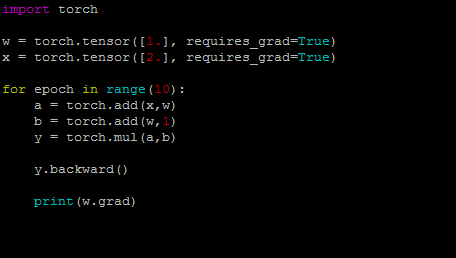
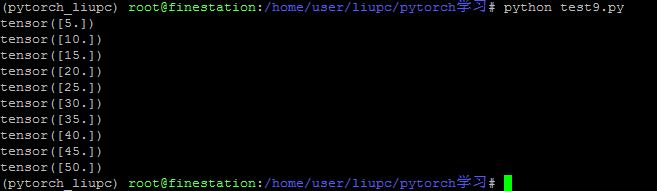
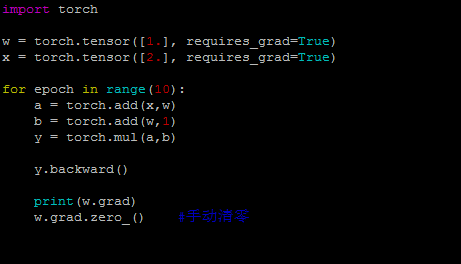
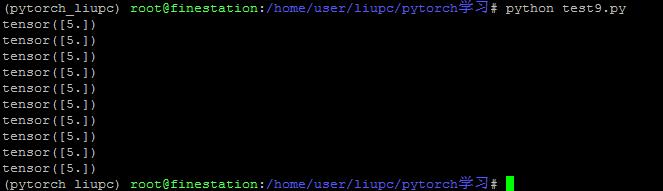
1. 梯度不会自动清零。再每次反向传播的时候会叠加上去，不会清零【例1】。需要手动的清零【例2】。

2. 依赖于叶子结点的结点，都是要求梯度的。求叶子节点的梯度需要用到这些结点的梯度。【例3】

3. 叶子节点不能执行原位操作。什么是原位操作呢？原位操作就是在原始内存中改变数据。【例4】

    为什么叶子节点不可以执行原位操作呢？比如下图，如果要求y对w的梯度，它是需要y对a的梯度的，而y对a的梯度等于w+1。因此在反向传播的时候是会用到w的，在前向传播的时候，会记录w的地址。反向传播的时候就是根据w的地址去找数。如果在反向传播之前，改变了地址当中的数据，那梯度求解肯定会出错。 

例1：

结果：

例2：

结果：

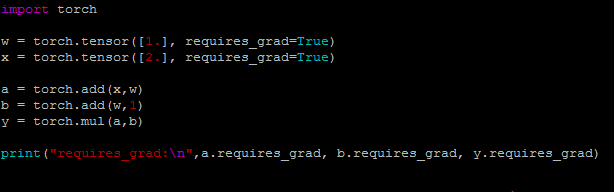
例3：

结果：

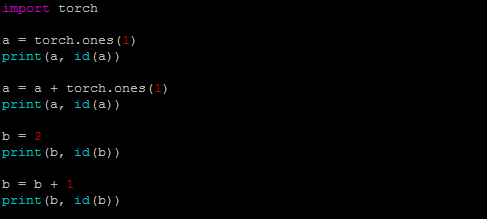
例4：a = a + torch.ones(1)，a的地址会发生改变

可以看到a地址发生了变化。

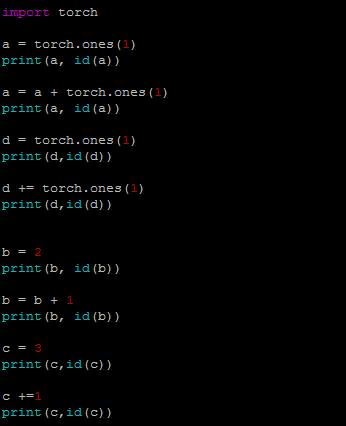
例5：a += torch.ones(1) 是原地操作

分析：

张量d执行了+=运算之后，地址不变。说明是原位操作。

而b和c是普通的Python变量，参见https://blog.csdn.net/pengchengliu/article/details/106390704