碰撞检测——GJK算法

Z时代
2024-01-10
分类：技术分享

基本概念

闵可夫斯基差（Minkowski difference）

凸体 $A$ 和 $B$

两个物体相交，当且仅当其闵可夫斯基差包含原点。

单纯形（simplex）

这里相当于在闵可夫斯基差内迭代形成一个多面体，且尽可能地使其包含原点。若其包含原点，则闵可夫斯基差包含原点，物体相交。

支持函数（support function）

s_X(vec{d}) = max{x cdot vec{d} | x in X }

即物体在方向 $vec{d}$ 上最远的点

有定理

算法

function GJK_intersection(shape p, shape q, vector initial_axis):
vector  A := Support(p, initial_axis) − Support(q, −initial_axis)
simplex s := {A}
vector  D := −A
loop:
A := Support(p, D) − Support(q, −D)
if dot(A, D) < 0:
reject
s := s ∪ A
s, D, contains_origin := SimplexOrigin(s)
if contains_origin:
accept

原点判定

线段

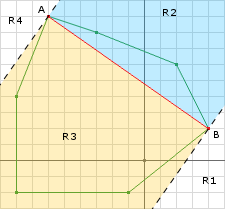
前面由 $OAcdot vec{d} < 0$ 判定过，所以原点不可能在 $R1$ 和 $R4$ 区域。那么若 $AB times AO times AB = vec{0}$ ，则原点在线段上。 $AB times AO times AB$ 的方向为垂直于 $AB$ 指向原点，作为下一次搜索方向。

三角形

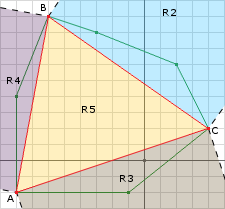
前面由 $OAcdot vec{d} < 0$ 判定过，所以原点不可能在 $R1$ （白色）区域。 $A$ 点为最新加入的点，即上次搜索方向为远离 $BC$ 指向 $A$ 的方向，所以原点不可能在 $R2$ 区域。

原点在 $R4$ 区域，当且仅当 $AC times AB times AB cdot AO > 0$ 。 $AC times AB times AB$ 的方向为垂直于 $AB$ 指向原点，作为下一次搜索方向。

原点在 $R3$ 区域，当且仅当 $AB times AC times AC cdot AO > 0$ 。 $AB times AC times AC$ 的方向为垂直于 $AC$ 指向原点，作为下一次搜索方向。

四面体（tetrahedron）

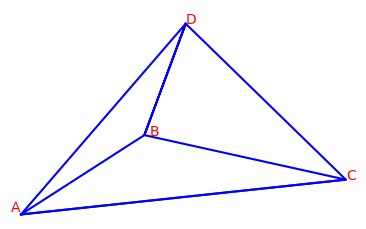
前面由 $OAcdot vec{d} < 0$ 判定过，所以原点不可能在 $BCD$ 面外部区域。

原点在四面体内当且仅当原点同时在面 $ACD$ 、面 $ABD$ 和面 $ABC$ 内部区域。比较点 $A$ 到各顶点的向量在该顶点所对的面的法向上的投影和点 $A$ 到原点的向量在该法向上的投影，判定原点是否在该面内部区域。

原点在 $ACD$ 面内区域当且仅当 $((AC times AD) cdot AB) cdot ((AC times AD) cdot AO) > 0$

原点在 $ABD$ 面内区域当且仅当 $((AB times AD) cdot AC) cdot ((AB times AD) cdot AO) > 0$

原点在 $ABC$ 面内区域当且仅当 $((AB times AC) cdot AD) cdot ((AB times AC) cdot AO) > 0$

若原点不在四面体内，那么必在其中一个面外区域，删除该面所对的顶点，剩下的进入上一步的三角形判定程序。

程序

constexprfloat EPSILON = 1e-6f;
Vector3f MinkowskiDifferenceSupport(const PolyhedralConvexShape &shape1,
const PolyhedralConvexShape &shape2, const Vector3f &dir)
{
Vector3f a = shape1.localGetSupportingVertex(dir);
Vector3f b = shape2.localGetSupportingVertex(-dir);
return a - b;
}
boolSimplex2(vector<Vector3f> &s, Vector3f &d)
{
Vector3f A = s[1];
Vector3f B = s[0];
Vector3f AB = B - A;
Vector3f AO =   - A;
Vector3f ABOO = AB.cross(AO).cross(AO); // norm to AB toward origin
if(ABOO.norm() <= EPSILON) // origin lies on
{
returntrue;
}
else
{
d = ABOO;
returnfalse;
}
}
boolSimplex3(vector<Vector3f> &s, Vector3f &d)
{
Vector3f A = s[2];
Vector3f B = s[1];
Vector3f C = s[0];
Vector3f AB = B - A;
Vector3f AC = C - A;
Vector3f AO =   - A;
Vector3f ABC = AB.cross(AC);
Vector3f ACBB = AC.cross(AB).cross(AB); // norm to AB toward far from C
Vector3f ABCC = AB.cross(AC).cross(AC); // norm to AC toward far from B
if(ACBB.dot(AO) > EPSILON) // origin lies on outside of AB
{
d = ACBB;
returnfalse;
}
if (ABCC.dot(AO) > EPSILON) // origin lies on outside of AC
{
d = ABCC;
returnfalse;
}
float dot = ABC.dot(AO); // origin lies in ABC region
if(dot > EPSILON)
{
d = ABC;
returnfalse;
}
elseif(dot < EPSILON)
{
d = -ABC;
returnfalse;
}
else// origin lies in ABC triangle
{
returntrue;
}
}
boolSimplex4(vector<Vector3f> &s, Vector3f &d)
{
Vector3f A = s[3];
Vector3f B = s[2];
Vector3f C = s[1];
Vector3f D = s[0];
Vector3f AO =   - A;
Vector3f AB = B - A;
Vector3f AC = C - A;
Vector3f AD = D - A;
Vector3f ABC = AB.cross(AC); // normal to ABC
Vector3f ACD = AC.cross(AD); // normal to ACD
Vector3f ADB = AD.cross(AB); // normal to ADB
float AD_ABC = ABC.dot(AD); // AD project on normal of ABC
float AB_ACD = ACD.dot(AB); // AB project on normal of ACD
float AC_ADB = ADB.dot(AC); // AC project on normal of ADB
float AO_ABC = ABC.dot(AO); // AO project on normal of ABC
float AO_ACD = ACD.dot(AO); // AO project on normal of ACD
float AO_ADB = ADB.dot(AO); // AO project on normal of ADB
bool inside_ABC = AD_ABC * AO_ABC > EPSILON;
bool inside_ACD = AB_ACD * AO_ACD > EPSILON;
bool inside_ADB = AC_ADB * AO_ADB > EPSILON;
if(inside_ABC && inside_ACD && inside_ADB) // origin inside tetrahedron
{
returntrue;
}
elseif(!inside_ABC) // origin outside ABC
{
// remove D
s[0] = s[1];
s[1] = s[2];
s[2] = s[3];
s.pop_back();
}
elseif(!inside_ACD) // origin outside ACD
{
// remove B
s[2] = s[3];
s.pop_back();
}
else// origin outside ADB
{
// remove C
s[1] = s[2];
s[2] = s[3];
s.pop_back();
}
return Simplex3(s, d);
}
boolSimplexOrigin(vector<Vector3f> &s, Vector3f &d)
{
bool contain_origin = false;
switch (s.size())
{
case2: // line segment
contain_origin = Simplex2(s, d);
break;
case3: // triangle
contain_origin = Simplex3(s, d);
break;
case4: // tetrahedron
contain_origin = Simplex4(s, d);
break;
default:
break;
}
return contain_origin;
}
boolgjkAlgorithm(const PolyhedralConvexShape &shape1,
const PolyhedralConvexShape &shape2)
{
// center difference as initial direction
Vector3f dir = shape1.getCenter() - shape2.getCenter();
if(dir.norm() < 0.001f)
dir = Vector3f{1.0f, 0.f, 0.f};
dir.normalize();
// init
vector<Vector3f> simplex;
simplex.reserve(4);
Vector3f simplex_point = MinkowskiDifferenceSupport(shape1, shape2, dir);
simplex.push_back(simplex_point);
dir = -simplex_point;
// main loop
int max_iteration = max(shape1.getNumVertices(), shape2.getNumVertices());
while(max_iteration-- > 0)
{
simplex_point = MinkowskiDifferenceSupport(shape1, shape2, dir);
if(simplex_point.dot(dir) < 0)
returnfalse;
simplex.push_back(simplex_point);
if(SimplexOrigin(simplex, dir))
returntrue;
}
returnfalse;
}

测试

参考

[1] dyn4j: GJK (Gilbert–Johnson–Keerthi)

[2] BulletCollision/NarrowPhaseCollision/btGjkPairDetector.cpp

[3] wiki: Gilbert–Johnson–Keerthi distance algorithm

[4] E. G. Gilbert, D. W. Johnson and S. S. Keerthi, "A fast procedure for computing the distance between complex objects in three-dimensional space," in IEEE Journal on Robotics and Automation, vol. 4, no. 2, pp. 193-203, April 1988, doi: 10.1109/56.2083

[5] Christer Ericson. 2004. Real-Time Collision Detection. CRC Press, Inc. USA. Chapter 9.5, pp. 399-410.

以上是碰撞检测——GJK算法的全部内容，来源链接： utcz.com/a/29640.html