VMD变分模态分解原理及R语言应用示例

• Z时代
• 2024-01-10
• 分类：技术分享

变分模态分解(variational mode decomposition，VMD)是一种新的信号分解估计方法，其整体框架是变分问题，使得每个模态的估计带宽之和最小，其中假设每个‘模态’是具有不同中心频率的有限带宽，为解决这一变分问题，采用了交替方向乘子法，不断更新各模态及其中心频率，逐步将各模态解调到相应的基频带，最终各个模态及相应的中心频率被一同提取出来。相比 EMD 和 LMD 的递归‘筛选’模式，VMD 将信号分解转化非递归、变分模态分解模式，并具有坚实的理论基础，其实质是多个自适应维纳滤波组，表现出更好的噪声鲁棒性。

VMD 的分解过程是变分问题的求解过程，该算法可分为变分问题的构造和求解，其中涉及了 3个重要概念：经典维纳滤波、希尔伯特变换和频率混合。

1. 受约束的变分问题如下：

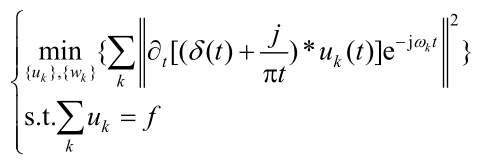
2. 变分问题的求解：

引入二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题变为非约束性变分问题：

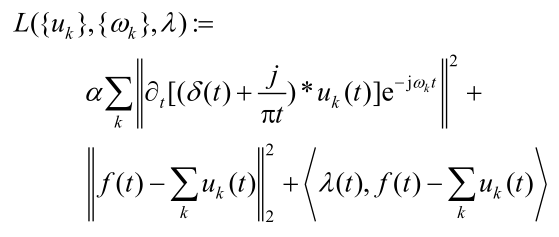
采用了乘法算子交替方向法(alternate direction method of multipliers)ADMM 解决以上变分问题，通过交替更新计算，求扩展拉格朗日表达式的‘鞍点’：

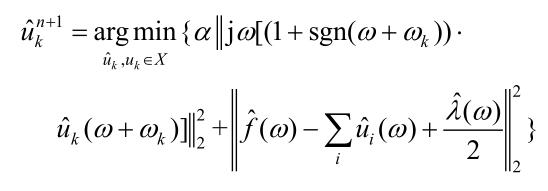
最终可整理为：

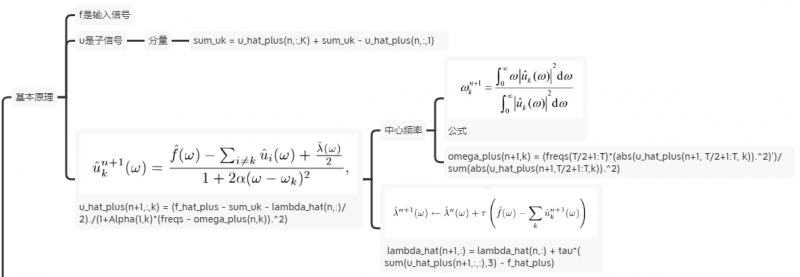
时间复杂度：

关于VMD(Variational Mode Decomposition)，具体原理可以参考其论文 :

K. Dragomiretskiy and D. Zosso, "Variational Mode Decomposition," in IEEE Transactions on Signal Processing, vol. 62, no. 3, pp. 531-544, Feb.1, 2014, doi: 10.1109/TSP.2013.2288675.

MATLAB code：

谱分解

rm(list = ls())
# install.packages("vmd")
library(vmd)
library(R.matlab)
ff <- "E:/office/......../data"
ff <- paste0(ff,"/", list.files(ff)[2])
mat<-readMat(ff)# str(mat)
m.u<-as.vector(mat$CH1)
m.i<-as.vector(mat$CH2)
plot.ts(m.i)
signal <- m.i
plot.ts(signal);rm(m.u,m.i,ff,mat)
依据傅里叶分析可知，这段数据包含了4个频谱，因此选择K=4+1
#tau=梯度步长
k=5; v = vmd(signal,alpha=length(signal),tau=0,DC=F,init=0,tol=1e-6,K=k,orderModes=TRUE)
# #To Data Frame
# df = as.data.frame(v)# head(df)
# #Plot Results# plot(v)
plot(v,facet='bymode',scales='free')

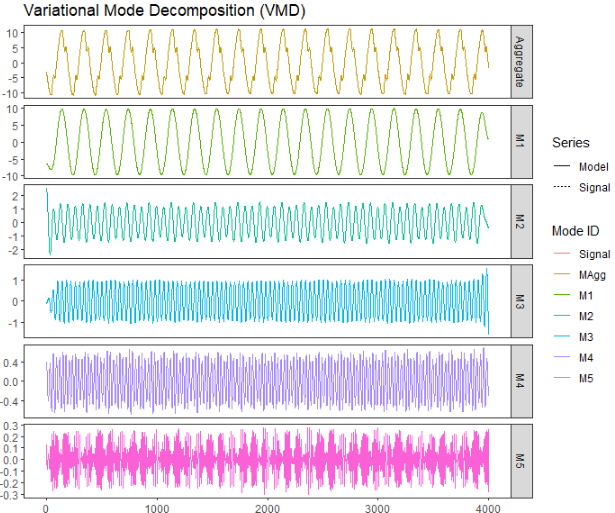
谱分解结果的收敛性

# #List of Results
l = v$getResult()  #  names(l)
#  u      - the collection of decomposed modes
#  u_hat  - spectra of the modes
#  omega  - estimated mode center-frequencies
# # compute HZ
ff <- 10^4
matplot(l$omega*ff,type = "l",ylab = "HZ")
text(dim(l$omega)[1],l$omega[dim(l$omega)[1],]*ff,
labels = round(l$omega[dim(l$omega)[1],],3)*ff,col = 1)

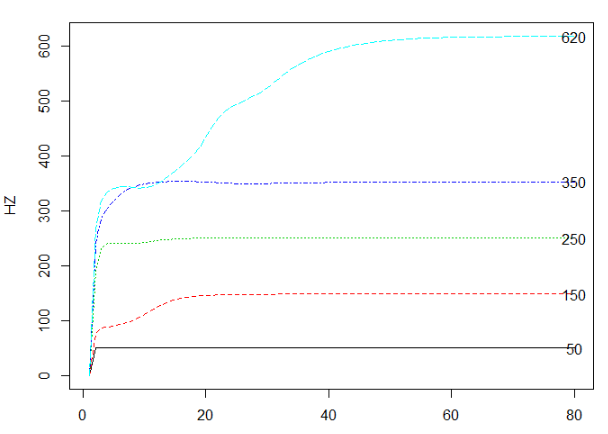
谱分解效果评估

v$plot.spectral.decomposition()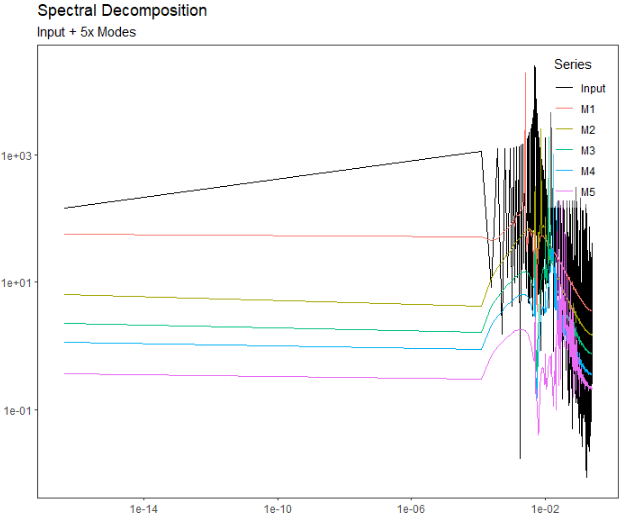

信息重构：

matplot(cbind(l$u[,1],rowSums(l$u[,2:4]),signal),type = "l",col = c(3,4,2) ,ylab = "amplitude")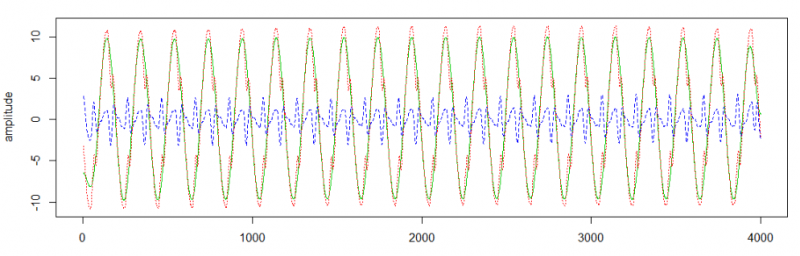

matplot(cbind(rowSums(l$u[,1:4]),signal),type = "l",col = c(4,2) ,ylab = "amplitude")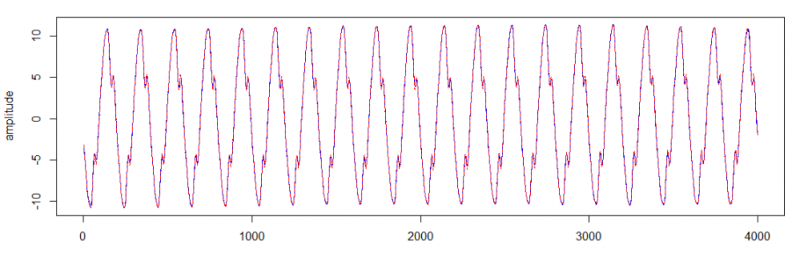

以上是 VMD变分模态分解原理及R语言应用示例 的全部内容， 来源链接： utcz.com/a/25681.html