字符串匹配算法原理(Hash、KMP、BM、Sunday)

引言

字符串的定位操作通常称作字符串的模式匹配，是各种字符串处理系统中最重要的操作之一，本文介绍Hash、KMP、BM、Sunday四种匹配算法。

字符串Hash

字符串Hash就是在字符串上进行哈希，可通俗理解为把字符串转为整数，最后构建理想状态下的一个整数对应一个字符串的单射。

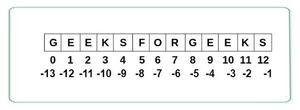
给定一个字符串S，我们规定:

index(x) = x -’a’+1

自然溢出法

自然溢出Hash公式为:

hash[i] = hash[i - 1] times p + index(s[i])

这里的hash数组利用了unsigned long long的自然溢出对(2^{64} - 1)取模。

单Hash法

单hash公式为:

hash[i] = (hash[i - 1]) times p + index(s[i]) % mod

其中p和mod均为素数，且p<mod，为了降低hash冲突，可让p和mod尽量往大取。

当一个哈希值对应两个或多个字符串时出现哈希冲突

取素数可以有效避免冲突，可以参照以下例子：

设函数表达式为f(y, x) = y*x mod N

当N = 8，y = 2时：

2*1 mod 8=2

2*2 mod 8=4

2*3 mod 8=6

2*4 mod 8=0

2*5 mod 8=2

2*6 mod 8=4

2*7 mod 8=6

当N = 7，y = 2时：

2*1 mod 7=2

2*2 mod 7=4

2*3 mod 7=6

2*4 mod 7=1

2*5 mod 7=3

2*6 mod 7=5

可以看出取素数冲突变少了。

可选择的素数

双Hash法

将一个字符串用不同的mod hash两次，再将两个结果用一个二元组表示，构成一个<hash1[i],hash2[i]>到字符串的理想单射，公式为:

hash1[i]=(hash1[i])times p+index(s[i]) % mod1

hash2[i]=(hash2[i])times p+index(s[i]) % mod2

字符串hash的获取

根据定义可以得出:

hash[1]=s_1

hash[2]=s_1times p+s_2

hash[3]=s_1times p^2+s_2times p+s_3

hash[4]=s_1times p^3+s_2times p^2+s_3times p+s_4

又由

hash[3,4]=s_3times p+s_4

hash[4]=s_1times p^3+s_2times p^2+s_3times p+s_4

hash[2]=s_1times p+s_2

可以得出:

hash[3,4]=hash[4]-hash[2]times p^2

所以得出通式为:

hash[l,r]=hash[r]-hash[l-1]times p^{r-l+1}

又因为每次都要取模，并且做减法时有可能出现负数，所以对其加mod后再取余做出修正，得到求字符串hash的最终公式为:

hash[l,r]=((hash[r]-hash[l-1]times p^{r-l+1}) % mod+mod) % mod

KMP

字符串查找算法(Knuth-Morris-Pratt )，简称为KMP算法，常用于在一个文本串S内查找一个模式串P 的出现位置，时间复杂度为O(n+m)，其中n为文本串的长度，m为模式串的长度。

KMP算法需要先寻找模式串中最长相等的前缀和后缀lps。

假设模式串P为: "bcdebcd"

可找到的前缀prefix有: "b"、"bc"、"bcd"、"bcde"

可找到的后缀suffix有: "d"、"cd"、"bcd"、"ebcd"

可得出lps为: "bcd"

因此可以根据模式串的lps来建立dp数组储存字符串再次出现的位置:

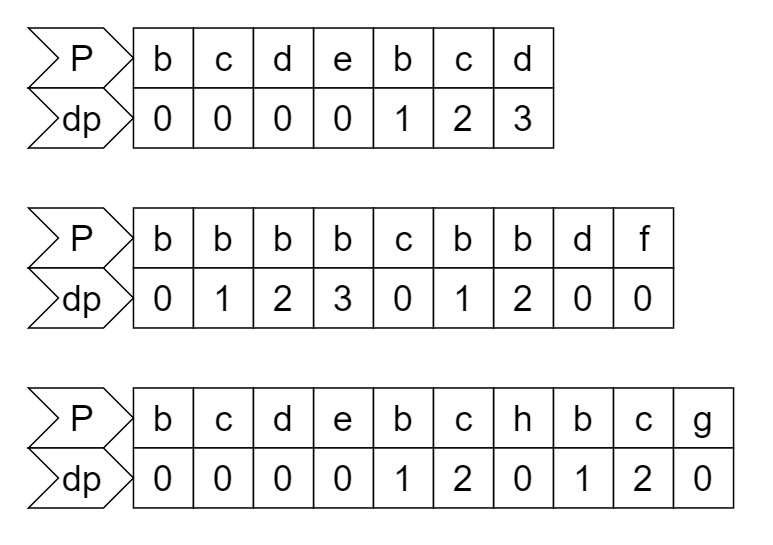
设文本串S为"bcbcdbcdbcbcbce"，模式串P为"bcbce"，模式串的dp数组为[0,0,1,2,0],匹配过程如下:

step1:

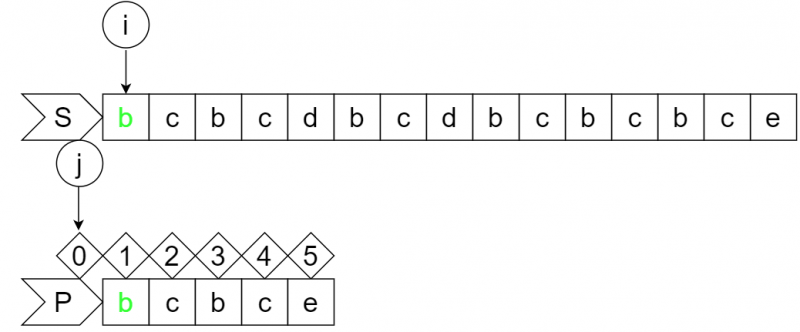
此时S串的i位字符与P串的j+1位字符匹配，i和j分别前进一位。

step2:

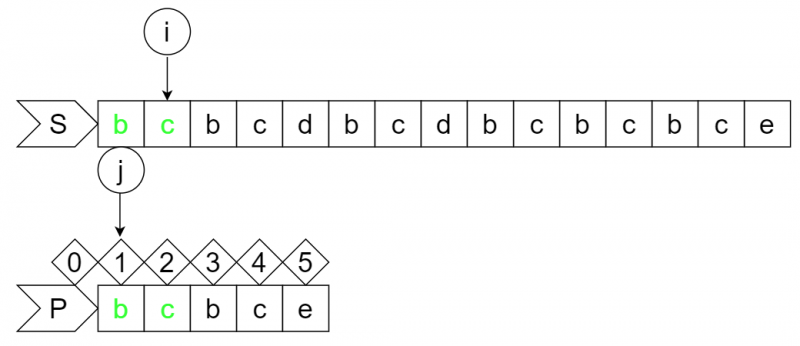
依次进行匹配......

step5:

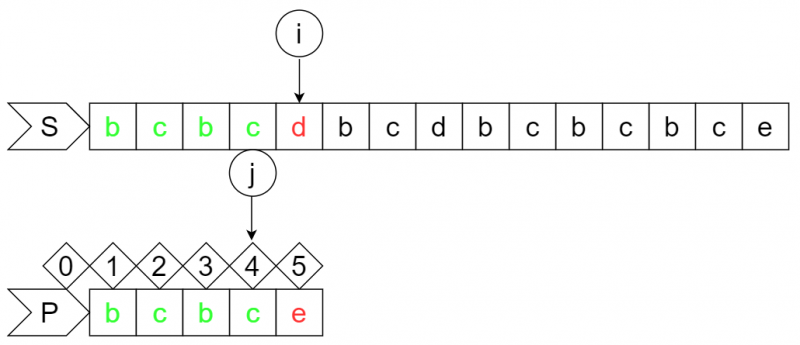
此时S串的i位字符为"d"，P串的j+1位字符为"e"，匹配失败，根据dp数组，字符"c"在P串的2号位出现过，j要从4号位回退到2号位，所以P串向右移动2位，i不变。

step6:

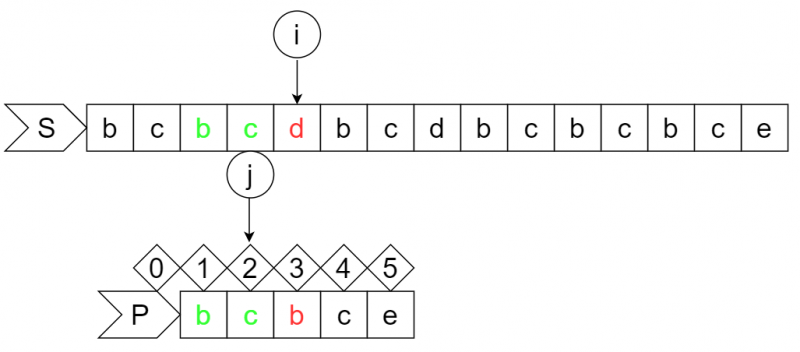
此时S串的i位字符"d"与P串的j+1位字符"b"失配，因为dp数组中字符"c"在之前没有出现过，则j要回退到0号位，所以P串向右移动2位，i不变。

step7:

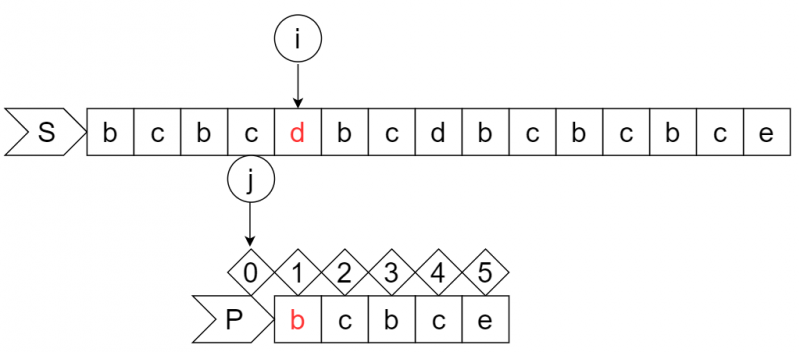
接上一步，S串的i位字符与P串的j+1位字符失配，因为j已经回退到了0号位，不能再回退，所以让i前进一位。

step8:

再依次进行匹配

step9:

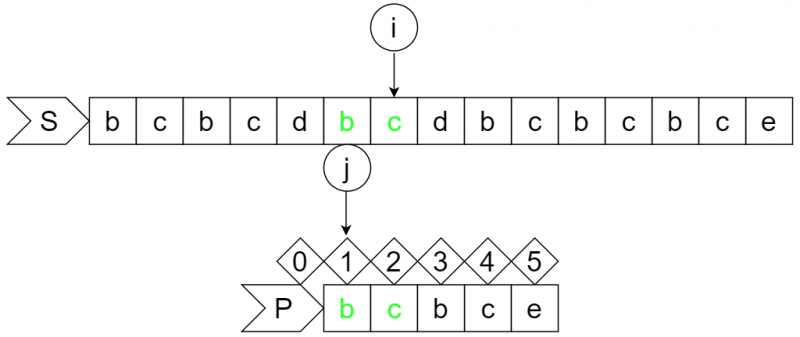
step10:

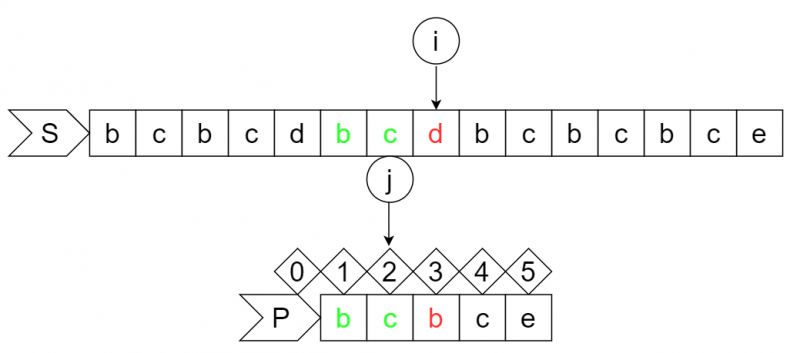
此时S串的i位字符为"d"，P串的j+1位字符为"b"，匹配失败，根据dp数组要让j回退到0号位，所以模式串向右移动2位，i不变。

step11:

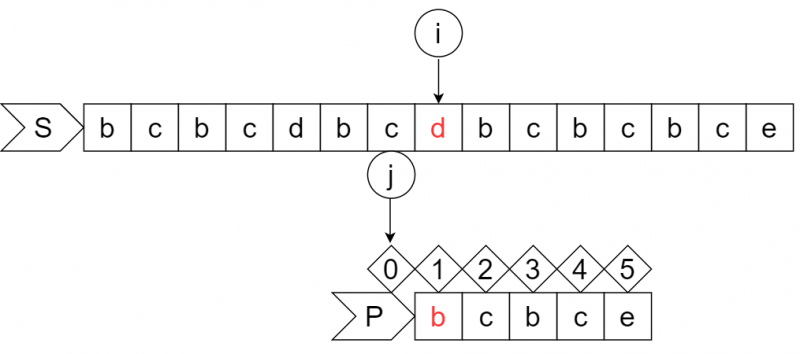
根据规则再依次进行匹配

step12:

......

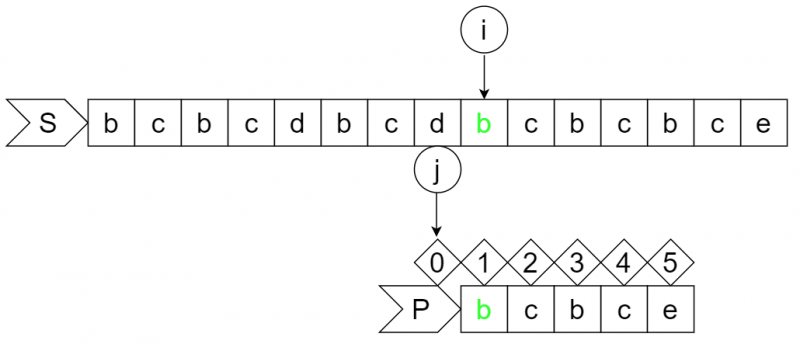
step19:

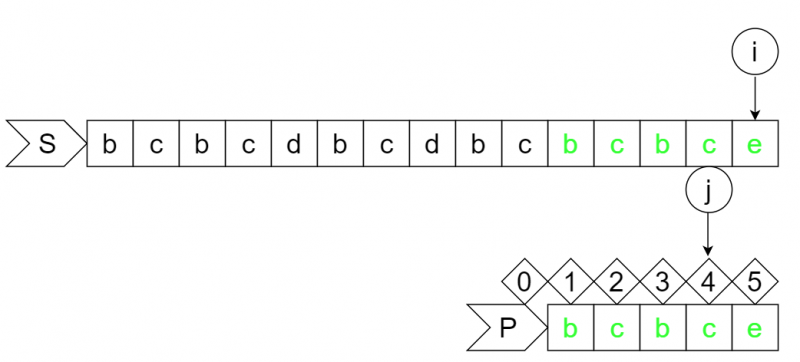
此时S串的i位字符为最后一个字符"e"，P串的j位于的4号位，i位字符与j+1位字符匹配，则i和j分别再前进一位。

step20:

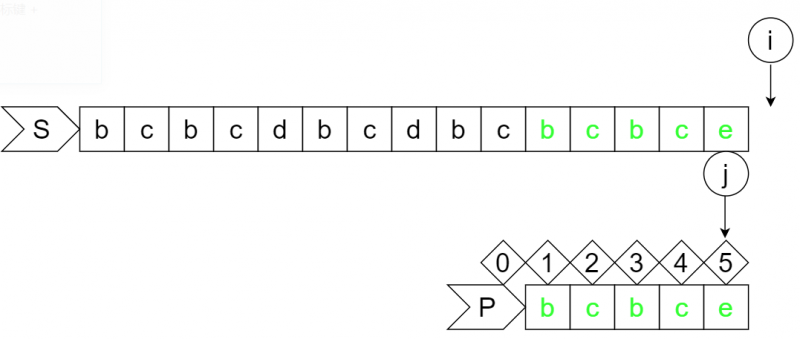
此时i已超出S串的边界，j位于P串的5号位，且等于P串的长度，则整个字符串匹配成功。

如果我们把匹配转移和失配转移用有限状态自动机(FSM)的形式来表示，根据模式串bcbce的dp数组[0,0,1,2,0]可以得出下面一个状态转移图:

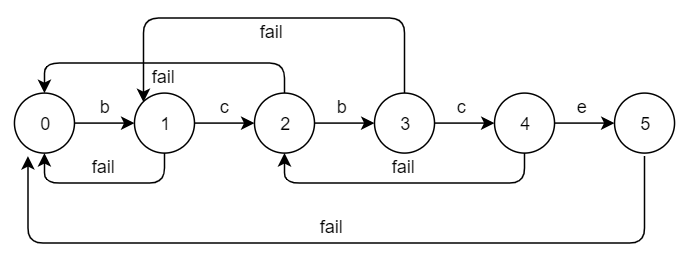
注意这里进行文本串遍历的i与BF算法(即暴力(Brute Force)算法)进行文本串遍历的i不同，BF算法进行文本串遍历的i是指起始位置，KMP算法进行文本串遍历的i是指当前匹配到的位置。

BM

BM(Boyer-Moore)算法则与KMP算法不同，KMP算法的模式串是从前往后遍历，BM算法的模式串是从后往前遍历。BM算法的时间复杂度最好为O(n/m)，最坏为O(nm)，其中n为文本串的长度，m为模式串的长度。BM算法有两条规则，分别是坏字符串规则(Bad character rule)和好前缀规则(Good suffix rule)，根据这两条规则相互竞争来进行字符串匹配。

坏字符串规则

当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数等于坏字符在模式串对应的位置减去坏字符在模式串中最右出现前的位置(注意该字符要在失配的字符位置之前)。此外，如果"坏字符"不包含在模式串之中，则将模式串直接整体对齐到这个字符的后方，继续比较。坏字符针对的是文本串。

设文本串S为"GCTTCTGCTACCTTTTGCGC"，模式串P为"CCTTTTGC"，坏字符串匹配规则如下:

当S串中有对应的坏字符"C"时，让P串中最靠右的与坏字符相配的字符"C"与S串中的坏字符对齐，P串相应的向右移动3位(坏字符"C"在P串中的位置4减去坏字符在P串中最右出现的位置1等于3)。

step1:

如果P串中没有出现S串中的那个坏字符，则将模式串直接整体对齐到这个字符的后方，继续比较。

step2:

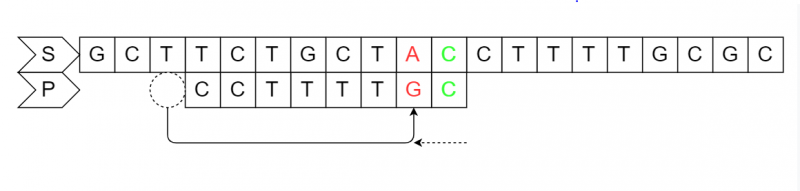
移动之后整个字符串匹配成功。

step3:

好后缀规则

当字符失配时，后移位数等于好后缀在模式串中的位置减去好后缀在模式串上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。好后缀针对的是模式串。

设文本串S为"CGTGCCTACTTACTTACTTA"，模式串P为"CTTACTTAC"，好后缀匹配规则如下:

当P串中存在已经匹配成功的好后缀"TAC"，因为要把目标串(上一个"TAC")对齐到好后缀现在的位置，所以P串向右移动的位数为好后缀在P串中的位置6减去好后缀在P串中上一次出现的位置2等于4，然后从P串的最尾元素开始往前匹配。

step1:

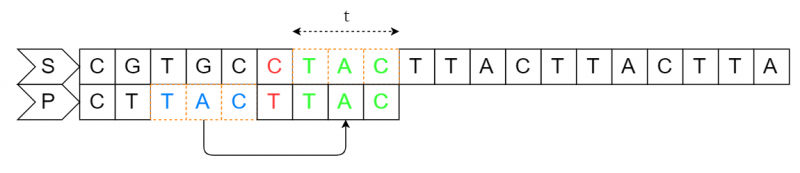
根据规则进行匹配

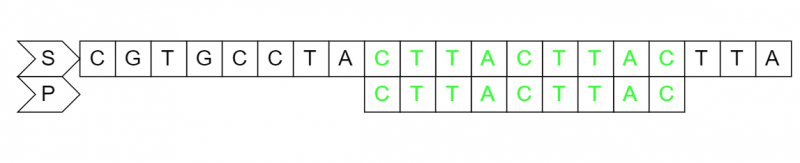
step2:

移动之后整个字符串匹配成功。

step3:

BM算法结合了坏字符串规则(bc)与好后缀规则(gs)来进行遍历，每一步对比两个规则可跳过的字符数，跳过字符数多的则为此步采用的策略，下一步模式串再从右向左依次与文本串相应位置的字符匹配，注意文本串是从左往右遍历，模式串是从右往左遍历。

设文本串S为"GTTATAGCTGATCGCGGCGTAGCGGCGAA"，模式串P为"GTAGCGGCG"，BM算法匹配过程如下:

初始时刻，P串的最后一个字符与S串对应位置的字符失配，如果采用bc可跳过6个字符，而采用gs则不能跳过字符，所以采用bc将P串向右移动，使模式串中与坏字符相配的字符与坏字符对齐。

step1:

此刻P串中的最后三个字符"GCG"与S串对应位置的字符匹配，但是到P串的第四个字符则与S串对应的字符失配，如果此时采用bc不能跳过字符，P串只能向右移动1位，但是采用gs可以发现P串中有以之对应的好后缀"GCG"，此时可以将前一个"GCG"向后移动到现有"GCG"的位置，跳过的字符数为2位，所以采用gs来移动P串。

step2:

接上一步之后，P串中的最后六个字符"GCGGCG"与S串对应位置的字符匹配，但是到P串的第七个字符"A"与S串对应位置的字符"C"失配，此时如果采用bc，因为失配的P串位置之前已经没有了与S串中坏字符"C"相配的字符，所以要将整个P串移动到坏字符之后的位置，只跳过了2个字符，但是采用gs则可以跳过7个字符，因为P串中失配的字符位置之前只有一个与好后缀对应的字符"G"，所以要将P串开头的"G"对齐到现有最末尾"G"的位置，整体位置移动跳过了7个字符，所以此步采用gs来移动P串。

step3:

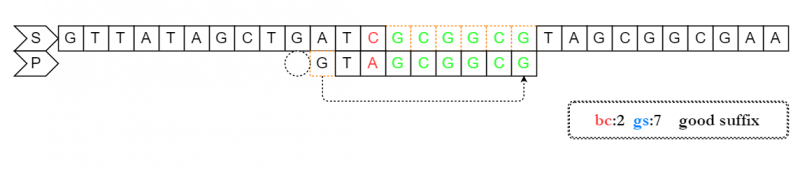
移动之后整个模式串匹配成功。

step4:

坏字符串规则和好后缀规则可以分开来采用，一般去除坏字符串规则，因为如果字符串很长的话，采用坏字符串规则内存开销非常大。

Sunday

Sunday算法的思想和BM算法很相似，只不过Sunday算法中模式串是从左往右匹配，在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符，规则为:

  • 如果该字符没有在模式串中出现则直接跳过，移动位数等于模式串长度加1

  • 如果该字符在模式串中出现，其移动位数等于模式串长度减去该字符在模式串中最后出现的位置(模式串中字符位置从0开始累加)。

Sunday算法需要建立一个偏移表，偏移表的作用是存储每一个字符的偏移量。设P为模式串，m为模式串长度，w为字符，则偏移量计算公式为:

shift[w]begin{cases} m-max { i<m|P[i]=w } quad if w is in P[0..m-1]\ m+1 qquad qquad qquad qquad quad otherwise\ end{cases}

例如P="leetcode":

m=8

shift[l] = 8 - max(l的位置) = 8 - 0 = 8

shift[e] = 8 - max(e的位置) = 8 - 2 = 6

shift[t] = 8 - max(t的位置) = 8 - 3 = 5

shift[c] = 8 - max(c的位置) = 8 - 4 = 4

shift[o] = 8 - max(o的位置) = 8 - 5 = 3

shift[d] = 8 - max(d的位置) = 8 - 6 = 2

shift[其他] = m + 1 = 8 + 1 = 9

设文本串S为"ATTAAGGCACATAC"，模式串P为"ACAT"，模式串中字符的偏移量为:

shift[A] = 4 - max(A的位置) = 4 - 2 = 2

shift[C] = 4 - max(C的位置) = 4 - 1 = 3

shift[T] = 4 - max(t的位置) = 4 - 3 = 1

Sunday算法匹配过程如下:

step1:

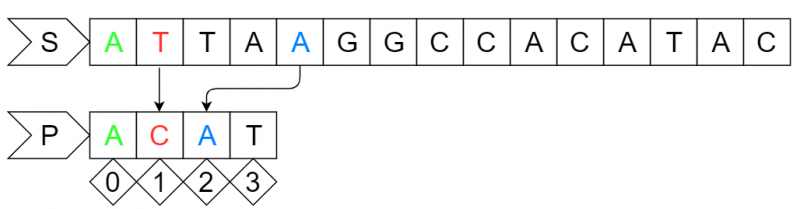
此时P串的第2个字符"C"与S串的第2个字符"T"失配，关注S串中参加匹配的最末位字符的下一位字符"A"，此时P串中有字符"A"，且最后出现在2号位，偏移量为P串的长度4减去字符"A"在P串中最后出现的位置2等于2位，所以将P串向右移动2位。

step2:

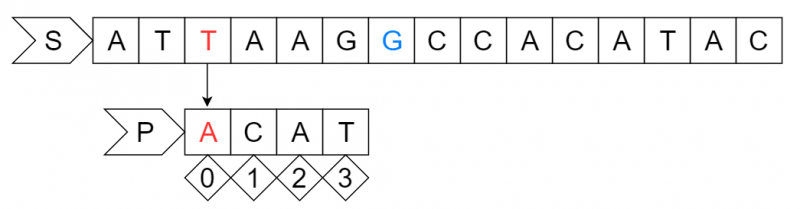
移动之后P串的第1个字符"A"与S串对应位置的字符"T"失配，关注S串中参加匹配的最末位字符的下一位字符"G"，但因为P串中没有字符"G"，偏移量为P串的长度4加1等于5位，所以P串向右移动5位。

step3:

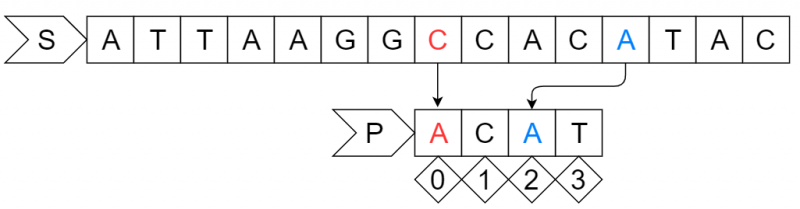
移动之后P串的第1个字符"A"与S串对应位置的字符"C"失配，关注S串中参加匹配的最末位字符的下一位字符"A"，此时P串中有字符"A"，且最后出现在2号位，偏移量为P串的长度4减去2等于2位，所以将P串向右移动2位。

step4:

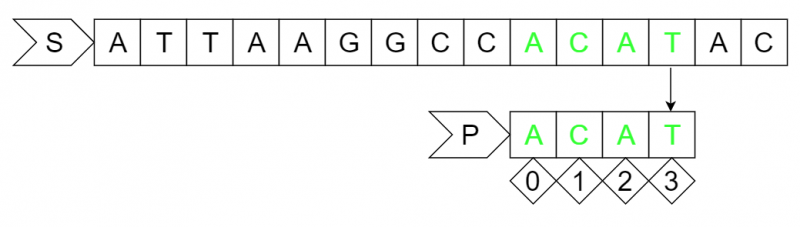
移动之后整个字符串匹配成功。

END

字符串匹配尽量先写KMP，如果KMP被卡了，就写Hash，如果Hash还不行，就试试BM。虽然Sunday算法很快，但是最常用的还是KMP和Hash。

以上是 字符串匹配算法原理(Hash、KMP、BM、Sunday) 的全部内容， 来源链接： utcz.com/a/19394.html

回到顶部