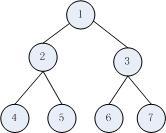
二叉树面试题

我之前面试了好几家公司，都会考一些关于二叉树的面试题，比如下面这几个面试题：

  1. 二叉树有哪几种遍历方式

  2. 不用递归如何遍历二叉树

  3. 如何判断二叉树是对称二叉树

  4. 将二叉树左右节点翻转

  5. 实现一个函数接收任意二叉树，求二叉树所有根节点到叶子路径组成的数字之和

前端常考的算法题就是二叉树和排序了，这些好像很多公司都会有一两道这样的题目，大家面试前可以重点看一下这些知识点，这篇文章主要讲解二叉树。

基础知识

了解二叉树之前我们先要知道什么是二叉树和二叉树的组成。

二叉树是每个节点不超过两个。一棵最上面的节点称为根节点，如果一个节点下面连接多个节点，那么该节点称为父节点，它下面的节点称为子节点，一个节点可以有0个或多个子节点，没有任何子节点的节点称为叶子节点

下面代码就是创建二叉树的过程。

functionNode(value, left, right) {
this.value = value;
this.left = left;
this.right = right;
}
functionBST() {
this.root = null;
this.insert = insert;
}
functioninsert(value) {
let node = new Node(value, null, null)
if (this.root == null) {
// 根节点
this.root = node;
} else {
// 子节点
let current = this.root;
let parent;
while (true) {
parent = current;
if (value < current.value) {
current = current.left;
if (current == null) {
parent.left = node;
break;
}
} else {
current = current.right;
if(current == null) {
parent.right = node;
break;
}
}
}
}
}
let tree = new BST()
tree.insert(1)
tree.insert(2)
tree.insert(3)
tree.insert(4)
console.log(tree.root)
复制代码

insert 方法是向二叉树中出入一个节点，我们需要判断节点的位置，分别对比左右节点的大小关系，然后选择性的输入到其中。

实战题目

文章的开头有5道面试题，下面开始做题啦！

问：二叉树有哪几种遍历方式？

答：有三种遍历方式，中序，先序，后序。中序遍历按照节点上的键值，以升序访问二叉树上的所有节点。先序遍历先访问根节点，然后以同样方式访问左子树和右子树。后序遍历先访问叶子节点，从左子树到右子树，再到根节点。

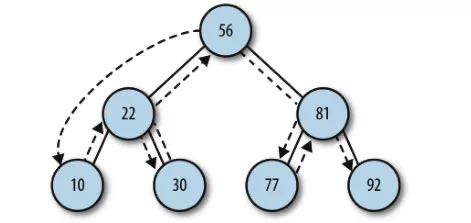
下图是中序遍历的路径图，10->22->30->56->77->81->92（按照升序访问的规则）

关于二叉树的面试题

// 中序遍历
functioninOrder(node) {
let result = []
if (!(node == null)) {
inOrder(node.left)
result.push(node.value)
inOrder(node.right)
}
return result
}
let tree = new BST()
tree.insert(56)
tree.insert(22)
tree.insert(81)
tree.insert(10)
tree.insert(30)
tree.insert(77)
tree.insert(92)
inOrder(tree.root)
复制代码

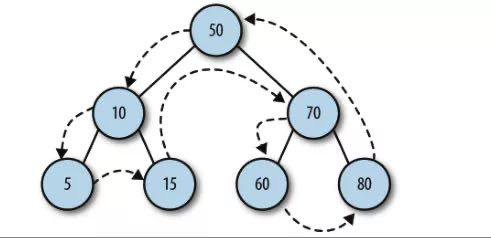
下图是先序遍历的路径图，50->10->5->15->70->60->80（按照先根节点再子节点）

关于二叉树的面试题

// 先序遍历
functionpreOrder(node) {
let result = []
if (!(node == null)) {
result.push(node.value)
preOrder(node.left)
preOrder(node.right)
}
return result
}
let tree = new BST()
tree.insert(50)
tree.insert(10)
tree.insert(70)
tree.insert(5)
tree.insert(15)
tree.insert(60)
tree.insert(80)
preOrder(tree.root)
复制代码

下图是后序遍历的路径图，3->22->16->37->99->45->23（按照先子节点再根节点）

关于二叉树的面试题

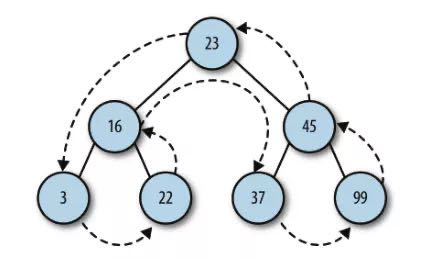
// 后序遍历
functionpostOrder(node) {
let result = []
if (!(node == null)) {
postOrder(node.left)
postOrder(node.right)
result.push(node.value)
}
return result
}
let tree = new BST()
tree.insert(23)
tree.insert(16)
tree.insert(45)
tree.insert(3)
tree.insert(22)
tree.insert(37)
tree.insert(99)
postOrder(tree.root)
复制代码

问：不用递归如何遍历二叉树？

其实代码中的 insert 方法就是没有使递归而是使用 while 循环进行遍历的，不知道你注意到了没有。下面我再通过使用 while 实现遍历。

使用循环遍历二叉树还必须使用栈进行回溯算法。

// 中序遍历
functioninOrder(node) {
let stack = []
let result = []
let parent = node;
while (parent !== null || stack.length) {
if (parent !== null) {
stack.push(parent)
parent = parent.left
} else {
parent = stack.pop()
result.push(parent.value)
parent = parent.right
}
}
console.log(result)
}
复制代码

// 先序遍历
functionpreOrder(node) {
let stack = []
stack.push(node)
let result = []
while (stack.length !== 0) {
let parent = stack.pop()
if (parent.right !== null) {
stack.push(parent.right)
}
if (parent.left !== null) {
stack.push(parent.left)
}
result.push(parent.value)
}
console.log(result)
}
复制代码

// 后序遍历
functionpostOrder(node) {
let stack = []
stack.push(node)
let result = []
let parent = node
while (stack.length !== 0) {
parent = stack.pop()
if (parent.left !== null) {
stack.push(parent.left)
}
if (parent.right !== null) {
stack.push(parent.right)
}
result.unshift(parent.value)
}
console.log(result)
}
复制代码

这里有一篇文章《非递归实现二叉树先序、中序和后序遍历》讲解了代码实现的思路。但是是Java代码写的，哈哈！

如果你对栈数据结构不了解，可以阅读我之前写的一篇文章《关于JS括号匹配的面试题》。

关于二叉树的面试题

总结

先序：根左右，

中序：左根右，

后续：左右根。

这里在提一句，深度优先和广度优先的感念，

“深度优先搜索就是树的先序遍历”，“广度优先搜索就是树的按层遍历”。

关于二叉树的面试题

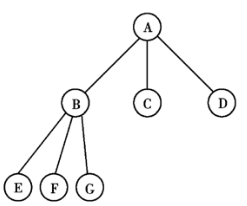
深度优先，先序遍历 ABEFGCD

广度优先，按层遍历 ABCDEFG

问：如何判断二叉树是对称二叉树

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

关于二叉树的面试题

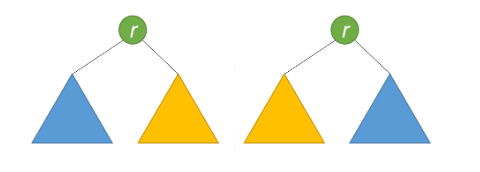
给定一个二叉树，检查它是否是镜像对称的。

var node1 = {
value: 1,
left: {
value: 2,
left: {
value: 3
},
right: {
value: 4
}
},
right: {
value: 2,
left: {
value: 4
},
right: {
value: 3
}
}
}
复制代码

递归

functionisSymmetric (root) {
return isMirror(root, root)
}
functionisMirror (t1, t2) {
if (t1 == null && t2 == null) returntrue;
if (t1 == null || t2 == null) returnfalse;
return (t1.value === t2.value) && isMirror(t1.right, t2.left) && isMirror(t1.left, t2.right)
}
console.log(isSymmetric(node1))
复制代码

问：将二叉树左右节点翻转

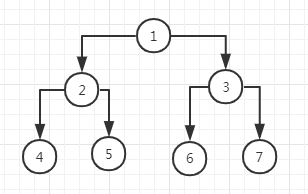
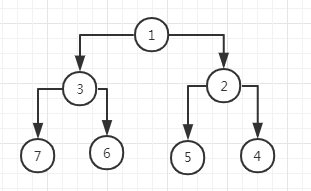
关于二叉树的面试题

关于二叉树的面试题

原题：二叉树的数据结构如下，需要将二叉树各节点左右翻转

var node1 = {
value: 1,
left: {
value: 2,
left: {
value: 4
},
right: {
value: 5
}
},
right: {
value: 3,
left: {
value: 6
},
right: {
value: 7
}
}
}
复制代码

思路：

  1. 先将左右节点交换位置

  2. 再递归子节点

functionreverse(node) {
if (node != null) {
let temp = node.left;
node.left = node.right;
node.right = temp;
reverse(node.left);
reverse(node.right);
}
}
复制代码

偷偷告诉你，这个题目是滴滴的面试题，感觉还挺难的！哈哈。

5、实现一个函数接收任意二叉树，求二叉树所有根节点到叶子路径组成的数字之和

functiongetPathSum(root) {
let total = 0
functionnext(node) {
if (node != undefined) {
total += node.value
next(node.left)
next(node.right)
}
}
next(root)
return total
}
复制代码

就是使用先序遍历完成

6、二叉树定义如下，实现函数 getPathSum(node)返回7=(1+2)+(1+3)

var node = {
value: 1,
left: {
value: 2,
left: null,
right: null
},
right: {
value: 3,
left: null,
right: null
}
}
复制代码

按照先序遍历

functiongetPathSum(root) {
let total = 0
let left = []
let right = []
functionnext(node, flag) {
if (node != undefined) {
if (flag === 0) {
left.push(node.value)
right.push(node.value)
total = node.value + node.value
}
if (flag === 1) {
left.push(node.value)
total += node.value
}
if (flag === 2) {
total += node.value
right.push(node.value)
}
next(node.left, 1)
next(node.right, 2)
}
}
next(root, 0)
return`${total}=(${left.join('+')})+(${right.join('+')})`
}
复制代码

这些就是我最近面试的一些题目，大家感觉怎么样？

哪里有问题，欢迎留言指正。

以上是 二叉树面试题 的全部内容， 来源链接： utcz.com/a/115383.html

回到顶部