【Java】JDK源码分析-TreeMap(2)
JDK源码分析-TreeMap(2)
WriteOnRead发布于 今天 03:00
1. 概述
前文「JDK源码分析-TreeMap(1)」分析了 TreeMap 的一些方法,本文分析其中的增删方法。这也是红黑树插入和删除节点的操作,由于相对复杂,因此单独进行分析。
2. 插入操作
该操作其实就是红黑树的插入节点操作。前面分析过,红黑树是一种平衡二叉树,新增节点后可能导致其失去平衡,因此需要对其进行修复操作以维持其平衡性。插入操作的代码如下:
public V put(K key, V value) {Entry<K,V> t = root;
// 若 root 节点为空,则直接插入(为根节点)
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
// 拆分 Comparator 接口和 Comparable 接口(上文 getEntry 方法也是如此)
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
// 若key已存在,则替换其对应的value
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 插入节点后的平衡性调整
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
对应的几种插入节点修复操作前文「数据结构与算法笔记(四)」已进行了分析,为了便于分析和理解代码,这里把图再贴一下(下图为关注节点的父节点是其祖父节点的左子节点的情况,在右边时操作类似):
- case1: 关注节点 a 的叔叔节点为红色
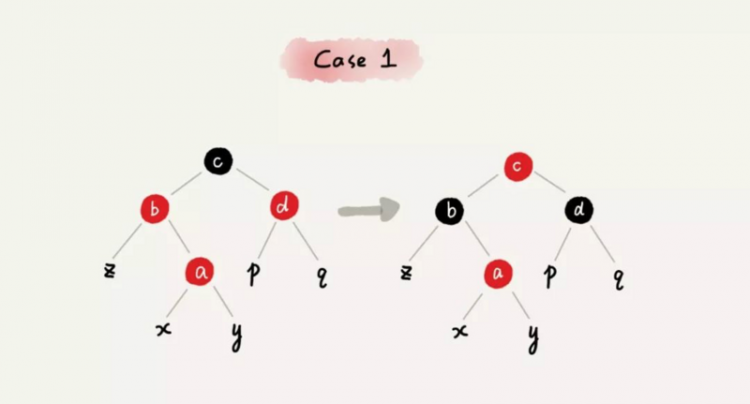
- case2: 关注节点为 a,它的叔叔节点 d 是黑色,a 是其父节点 b 的右子节点
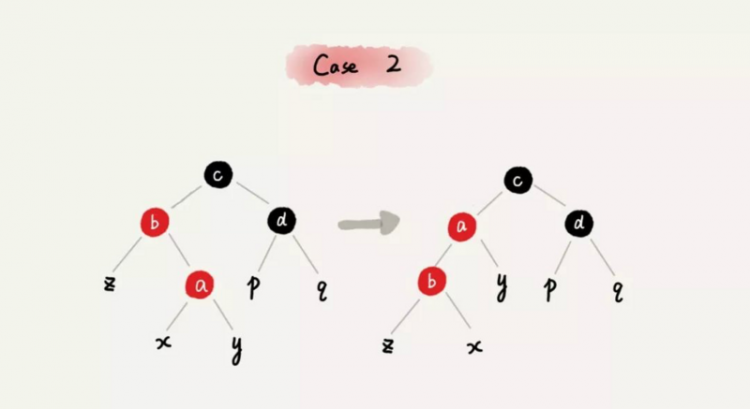
- case3: 关注节点是 a,它的叔叔节点 d 是黑色,a 是其父节点 b 的左子节点
插入操作的平衡调整代码如下:
private void fixAfterInsertion(Entry<K,V> x) {// 新插入的节点为红色
x.color = RED;
// 只有在父节点为红色时需要进行插入修复操作
while (x != null && x != root && x.parent.color == RED) {
// 下面两种情况是左右对称的
// x 的父节点是它祖父节点的左子节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// case1
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
// case2
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// case3
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
}
// x 的父节点是它祖父节点的右子节点(与上面情况对称)
else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
对称情况下的相应操作不再分析,其原理是类似的。
3. 删除操作
remove() 方法:
public V remove(Object key) {Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
deleteEntry 方法如下:
/*** Delete node p, and then rebalance the tree.
*/
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
// 左右子树都不为空,寻找后继节点
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
// 只有一个根节点
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
几种删除操作情况如下(下图为关注节点为父节点的左子节点的情况,关注节点为父节点的右子节点情况时的操作对称):
- case1: 关注节点的兄弟节点是红色
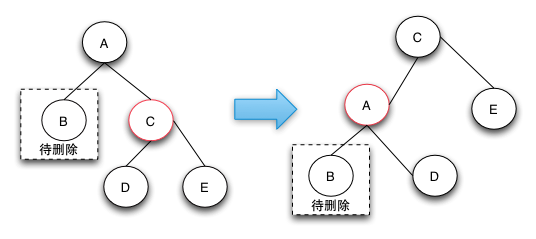
- case2: 关注节点的兄弟节点是黑色,且兄弟节点的子节点都是黑色
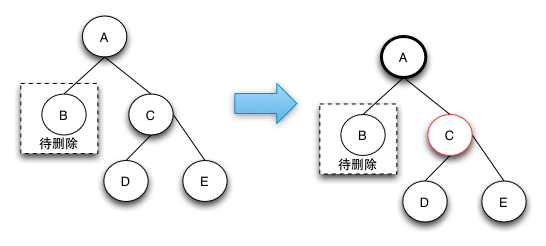
- case3: 关注节点的兄弟节点是黑色,且左子节点是红色、右子节点是黑色
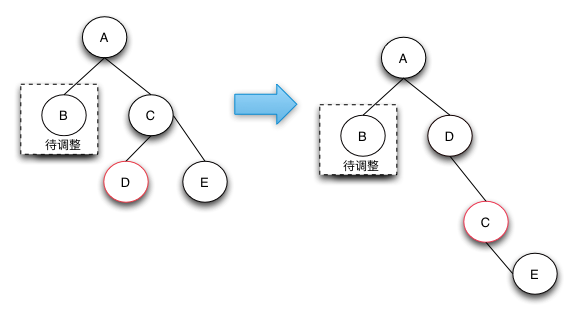
- case4: 关注节点的兄弟节点是黑色,且右子节点是红色、左子节点是黑色

删除操作的平衡调整代码如下:
private void fixAfterDeletion(Entry<K,V> x) {// x 不为根节点,且颜色为黑色
while (x != root && colorOf(x) == BLACK) {
// x 是父节点的左子节点
if (x == leftOf(parentOf(x))) {
// 兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
// case1 待删除节点的兄弟节点为红色
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
// case2 待删除节点的兄弟节点的子节点都为黑色
if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
// case3 待删除节点的兄弟节点的左子节点为红色、右子节为黑色
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// case4 待删除节点的兄弟节点的左子节点为黑色、右子节为红色
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK); //??
rotateLeft(parentOf(x));
x = root;
}
}
// x 是父节点的右子节点(对称操作)
else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
插入和删除操作相对复杂,容易被绕晕,但其实也是有规律可循的。对比操作的图解,可以更容易分析和理解。
参考文章:
https://zhuanlan.zhihu.com/p/...
这篇文章介绍了红黑树的删除操作,逻辑清晰,推荐阅读。
相关阅读:
JDK源码分析-TreeMap(1)
数据结构与算法笔记(四)

java后端
阅读 40发布于 今天 03:00
本作品系原创,采用《署名-非商业性使用-禁止演绎 4.0 国际》许可协议
WriteOnRead
微信公众号:WriteOnRead。
1 声望
0 粉丝
WriteOnRead
微信公众号:WriteOnRead。
1 声望
0 粉丝
宣传栏
目录
1. 概述
前文「JDK源码分析-TreeMap(1)」分析了 TreeMap 的一些方法,本文分析其中的增删方法。这也是红黑树插入和删除节点的操作,由于相对复杂,因此单独进行分析。
2. 插入操作
该操作其实就是红黑树的插入节点操作。前面分析过,红黑树是一种平衡二叉树,新增节点后可能导致其失去平衡,因此需要对其进行修复操作以维持其平衡性。插入操作的代码如下:
public V put(K key, V value) {Entry<K,V> t = root;
// 若 root 节点为空,则直接插入(为根节点)
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
// 拆分 Comparator 接口和 Comparable 接口(上文 getEntry 方法也是如此)
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
// 若key已存在,则替换其对应的value
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 插入节点后的平衡性调整
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
对应的几种插入节点修复操作前文「数据结构与算法笔记(四)」已进行了分析,为了便于分析和理解代码,这里把图再贴一下(下图为关注节点的父节点是其祖父节点的左子节点的情况,在右边时操作类似):
- case1: 关注节点 a 的叔叔节点为红色

- case2: 关注节点为 a,它的叔叔节点 d 是黑色,a 是其父节点 b 的右子节点

- case3: 关注节点是 a,它的叔叔节点 d 是黑色,a 是其父节点 b 的左子节点
插入操作的平衡调整代码如下:
private void fixAfterInsertion(Entry<K,V> x) {// 新插入的节点为红色
x.color = RED;
// 只有在父节点为红色时需要进行插入修复操作
while (x != null && x != root && x.parent.color == RED) {
// 下面两种情况是左右对称的
// x 的父节点是它祖父节点的左子节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// case1
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
// case2
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// case3
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
}
// x 的父节点是它祖父节点的右子节点(与上面情况对称)
else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
对称情况下的相应操作不再分析,其原理是类似的。
3. 删除操作
remove() 方法:
public V remove(Object key) {Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
deleteEntry 方法如下:
/*** Delete node p, and then rebalance the tree.
*/
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
// 左右子树都不为空,寻找后继节点
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
// 只有一个根节点
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
几种删除操作情况如下(下图为关注节点为父节点的左子节点的情况,关注节点为父节点的右子节点情况时的操作对称):
- case1: 关注节点的兄弟节点是红色

- case2: 关注节点的兄弟节点是黑色,且兄弟节点的子节点都是黑色

- case3: 关注节点的兄弟节点是黑色,且左子节点是红色、右子节点是黑色

- case4: 关注节点的兄弟节点是黑色,且右子节点是红色、左子节点是黑色

删除操作的平衡调整代码如下:
private void fixAfterDeletion(Entry<K,V> x) {// x 不为根节点,且颜色为黑色
while (x != root && colorOf(x) == BLACK) {
// x 是父节点的左子节点
if (x == leftOf(parentOf(x))) {
// 兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
// case1 待删除节点的兄弟节点为红色
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
// case2 待删除节点的兄弟节点的子节点都为黑色
if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
// case3 待删除节点的兄弟节点的左子节点为红色、右子节为黑色
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// case4 待删除节点的兄弟节点的左子节点为黑色、右子节为红色
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK); //??
rotateLeft(parentOf(x));
x = root;
}
}
// x 是父节点的右子节点(对称操作)
else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
插入和删除操作相对复杂,容易被绕晕,但其实也是有规律可循的。对比操作的图解,可以更容易分析和理解。
参考文章:
https://zhuanlan.zhihu.com/p/...
这篇文章介绍了红黑树的删除操作,逻辑清晰,推荐阅读。
相关阅读:
JDK源码分析-TreeMap(1)
数据结构与算法笔记(四)

以上是 【Java】JDK源码分析-TreeMap(2) 的全部内容, 来源链接: utcz.com/a/113835.html




得票时间